Що таке збалансована точність? (визначення & #038; приклад)

Збалансована точність – це показник, який ми можемо використовувати для оцінки продуктивності моделі класифікації .

Він розраховується таким чином:

Збалансована точність = (чутливість + специфічність) / 2

золото:

• Чутливість : «Справжній позитивний рівень» – відсоток позитивних випадків, які модель може виявити.
• Специфічність : «справжній негативний рівень» – відсоток негативних випадків, які модель може виявити.

Ця метрика особливо корисна, коли два класи незбалансовані, тобто один клас виглядає набагато більше, ніж інший.

У наведеному нижче прикладі показано, як розрахувати збалансовану точність на практиці, і показано, чому це така корисна метрика.

Приклад: обчислення збалансованої точності

Припустімо, що спортивний аналітик використовує модель логістичної регресії , щоб передбачити, чи будуть 400 різних студентських баскетболістів задрафтовані до НБА.

Наступна матриця плутанини узагальнює прогнози, зроблені моделлю:

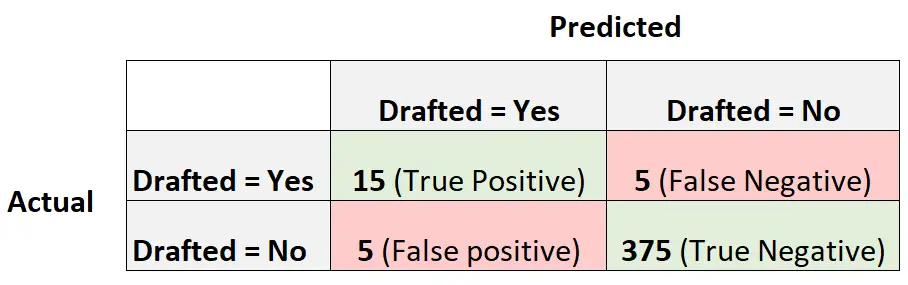
Щоб розрахувати збалансовану точність моделі, ми спочатку розрахуємо чутливість і специфічність:

• Чутливість : «справжній позитивний коефіцієнт» = 15 / (15 + 5) = 0,75
• Специфічність : «справжній негативний коефіцієнт» = 375 / (375 + 5) = 0,9868

Тоді ми можемо обчислити збалансовану точність наступним чином:

• Збалансована точність = (чутливість + специфічність) / 2
• Збалансована точність = (0,75 + 9868) / 2
• Збалансована точність = 0,8684

Збалансована точність моделі виявляється 0,8684 .

Зауважте, що чим ближче збалансована точність до 1, тим більше модель здатна правильно класифікувати спостереження.

У цьому прикладі збалансована точність досить висока, що говорить нам про те, що модель логістичної регресії дуже добре прогнозує, чи будуть задрафтовані студентські гравці в НБА.

У цьому сценарії, оскільки класи дуже незбалансовані (20 гравців були задрафтовані, а 380 – ні), збалансована точність дає нам більш реалістичну картину продуктивності моделі порівняно із загальним показником точності.

Наприклад, ми б обчислили точність моделі таким чином:

• Точність = (TP + TN) / (TP + TN + FP + FN)
• Точність = (15 + 375) / (15 + 375 + 5 + 5)
• Точність = 0,975

Точність моделі становить 0,975 , що здається надзвичайно високим.

Однак розглянемо модель, яка просто передбачає, що кожен гравець залишиться без драфту. Це матиме точність 380/400 = 0,95 . Це лише трохи нижче, ніж точність нашої моделі.

Збалансована оцінка точності 0,8684 дає нам краще уявлення про здатність моделі передбачати обидва класи.

Іншими словами, це дає нам краще уявлення про здатність моделі передбачити, які гравці залишаться без драфту , а які.

Додаткові ресурси

У наступних посібниках пояснюється, як створити матрицю помилок у різних статистичних програмах:

Як створити матрицю плутанини в Excel
Як створити матрицю плутанини в R
Як створити матрицю плутанини в Python