Як виконати зважену регресію найменших квадратів у r

Одне з ключових припущень лінійної регресії полягає в тому, що залишки розподіляються з рівною дисперсією на кожному рівні змінної предиктора. Це припущення відоме як гомоскедастичність .

Якщо це припущення не виконується, кажуть, що гетероскедастичність присутня в залишках. Коли це відбувається, результати регресії стають ненадійними.

Одним із способів вирішення цієї проблеми є використання зваженої регресії найменших квадратів , яка призначає ваги спостереженням таким чином, що ті з низькою дисперсією помилок отримують більшу вагу, оскільки містять більше інформації порівняно зі спостереженнями з більшою дисперсією помилок.

Цей підручник надає покроковий приклад того, як виконувати зважену регресію найменших квадратів у R.

Крок 1: Створіть дані

Наступний код створює кадр даних, що містить кількість вивчених годин і відповідну оцінку іспиту для 16 студентів:

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Крок 2: Виконайте лінійну регресію

Далі ми використаємо функцію lm() , щоб підібрати просту модель лінійної регресії , яка використовує години як змінну прогностику та оцінку як змінну відповіді :

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

Крок 3. Тест на гетероскедастичність

Далі ми створимо графік залишків і підігнаних значень, щоб візуально перевірити гетероскедастичність:

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

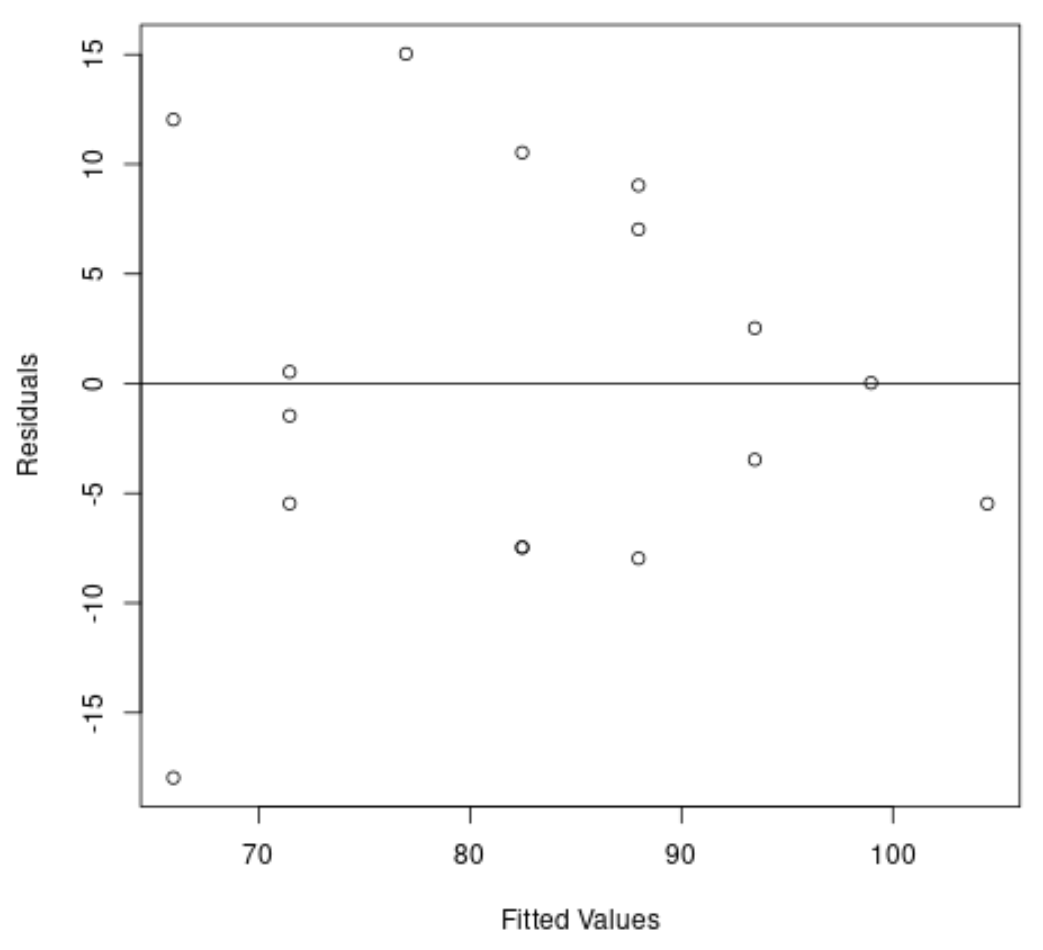
З графіка ми бачимо, що залишки мають форму «конуса»: вони не розподілені з рівною дисперсією по всьому графіку.

Щоб формально перевірити гетероскедастичність, ми можемо виконати тест Брейша-Пейгана:

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Тест Брейша-Пейгана використовує такі нульові та альтернативні гіпотези :

• Нульова гіпотеза (H ₀ ): наявна гомоскедастичність (залишки розподіляються з рівною дисперсією)
• Альтернативна гіпотеза ( _HA ): наявна гетероскедастичність (залишки не розподілені з рівною дисперсією)

Оскільки p-значення тесту становить 0,0466 , ми відхилимо нульову гіпотезу та зробимо висновок, що гетероскедастичність є проблемою в цій моделі.

Крок 4. Виконайте зважену регресію найменших квадратів

Оскільки гетероскедастичність присутня, ми виконаємо зважений метод найменших квадратів, встановивши ваги так, щоб спостереження з меншою дисперсією отримували більшу вагу:

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

З результатів ми бачимо, що оцінка коефіцієнта для змінної предиктора годин дещо змінилася, а загальна відповідність моделі покращилася.

Зважена модель найменших квадратів має залишкову стандартну помилку 1,199 порівняно з 9,224 у оригінальній моделі простої лінійної регресії.

Це вказує на те, що прогнозовані значення, отримані за допомогою моделі зважених найменших квадратів, набагато ближчі до фактичних спостережень порівняно з прогнозованими значеннями, отриманими за допомогою моделі простої лінійної регресії.

Зважена модель найменших квадратів також має R-квадрат 0,6762 порівняно з 0,6296 у вихідній моделі простої лінійної регресії.

Це вказує на те, що зважена модель найменших квадратів здатна пояснити більше розбіжностей в іспитових балах, ніж проста модель лінійної регресії.

Ці вимірювання вказують на те, що зважена модель найменших квадратів забезпечує кращу відповідність даних порівняно з моделлю простої лінійної регресії.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати квантильну регресію в R