Різниця між значеннями t і p в статистиці
Два терміни, які студенти часто плутають у статистиці, це t-values і p-values .
Щоб зрозуміти різницю між цими термінами, допоможе зрозуміти t-тест .
Загалом, існує три різні типи t-тестів:
- Т-критерій для однієї вибірки : використовується для перевірки того, чи дорівнює середнє значення генеральної сукупності певному значенню.
- T-критерій двох вибірок : використовується для перевірки рівності середніх двох генеральних сукупностей.
- Т-критерій для парних вибірок : використовується для перевірки того, чи середні значення двох генеральних сукупностей рівні, коли кожне спостереження в одній вибірці можна пов’язати зі спостереженням в іншій вибірці.
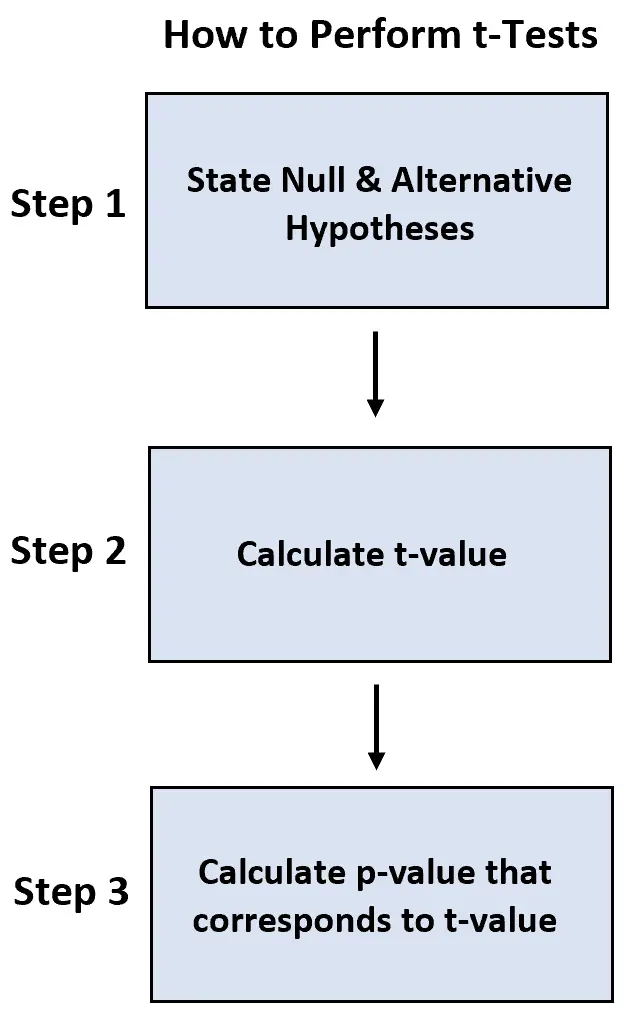
Для виконання кожного тесту ми використовуємо такі кроки:
- Крок 1: Сформулюйте нульову та альтернативну гіпотезу.
- Крок 2: Обчисліть значення t.
- Крок 3: обчисліть p-значення, яке відповідає t-значенню.
Для кожного тесту t-значення є способом кількісного визначення різниці між середніми сукупностями, а p-значення — це ймовірність отримання t-значення з абсолютним значенням, принаймні таким великим, як ми фактично спостерігали у «вибірці». даних, якщо нульова гіпотеза дійсно вірна.
Якщо p-значення менше певного значення (наприклад, 0,05), тоді ми відхиляємо нульову гіпотезу тесту.
Для кожного типу t-критерію нас цікавить p-значення , і ми просто використовуємо t-значення як проміжний крок для обчислення p-значення.
У наступному прикладі показано, як обчислити та інтерпретувати t-значення та відповідне p-значення для двовибіркового t-тесту.
Приклад: обчисліть та інтерпретуйте значення T і P
Припустімо, ми хочемо знати, чи однакова середня вага двох різних видів черепах. Ми збираємо просту випадкову вибірку з 12 черепах з кожної популяції з такими вагами:
Вид №1 : 301, 298, 295, 297, 304, 305, 309, 298, 291, 299, 293, 304
Вид №2 : 302, 309, 324, 313, 312, 310, 305, 298, 299, 300, 289, 294
Ось як виконати двовибірковий t-тест, використовуючи ці дані:
Крок 1: Сформулюйте нульову та альтернативну гіпотезу.
Спочатку ми сформулюємо нульову та альтернативну гіпотези:
- H 0 : μ 1 = μ 2 (два середні сукупності рівні)
- H 1 : μ 1 ≠ μ 2 (два середні сукупності не рівні)
Крок 2: Обчисліть значення t.
Далі ми введемо ваги кожної вибірки черепахи в калькулятор t-тесту для двох вибірок і знайдемо, що t-значення становить -1,608761 .
Крок 3: обчисліть p-значення.
Ми також можемо скористатися двовибірковим калькулятором t-тесту , щоб знайти, що p-значення, яке відповідає t-значенню -1,608761, дорівнює 0,121926 .
Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.
Це означає, що ми не маємо достатніх доказів того, що середня вага черепах у двох популяціях різна.
Зверніть увагу, що ми просто використовували t-значення як проміжний крок для обчислення p-значення. Р-значення — це справжнє значення, яке нас цікавило, але спочатку нам потрібно було обчислити t-значення.
Додаткові ресурси
Наступні навчальні посібники пропонують додаткову інформацію про t-тести та p-значення:
Вступ до одновибіркового t-критерію
Вступ до двовибіркового t-тесту
Знайомство з t-критерієм парних зразків
Як вручну обчислити значення P за t-тестом