Різниця між значеннями z і значеннями p в статистиці

Два терміни, які студенти часто плутають у статистиці, – це z-значення та p-значення .

Щоб зрозуміти різницю між цими термінами, допоможе зрозуміти z-тести .

Є два поширених типи z-тестів:

• Z-тест для однієї вибірки : використовується для перевірки того, чи дорівнює середнє значення сукупності певному значенню.
• Z-критерій двох вибірок : використовується для перевірки рівності двох середніх сукупностей.

Для виконання кожного тесту ми використовуємо такі кроки:

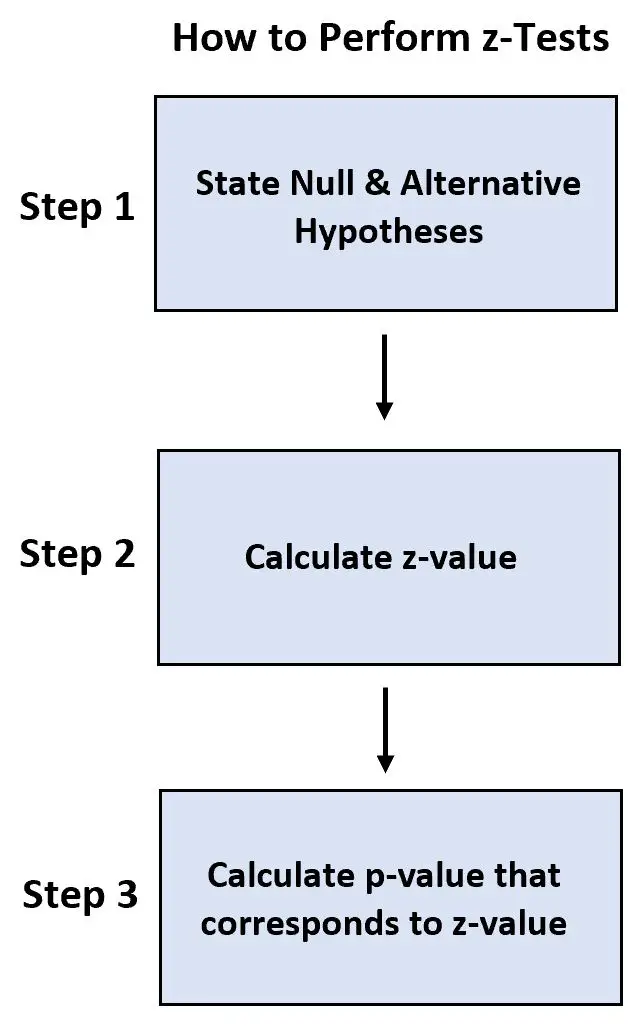
• Крок 1: Сформулюйте нульову та альтернативну гіпотезу.
• Крок 2: обчисліть значення z.
• Крок 3: обчисліть p-значення, яке відповідає z-значенню.

Для кожного тесту z-значення — це спосіб кількісної оцінки різниці між середніми сукупностями, а p-значення — це ймовірність отримання z-значення з абсолютним значенням, принаймні таким великим, як ми фактично спостерігали у «вибірці». даних, якщо нульова гіпотеза дійсно вірна.

Якщо p-значення менше певного значення (наприклад, 0,05), тоді ми відхиляємо нульову гіпотезу тесту.

Для кожного типу z-тесту нас цікавить p-значення , і ми просто використовуємо z-значення як проміжний крок для обчислення p-значення.

У наступному прикладі показано, як обчислити та інтерпретувати z-значення та відповідне p-значення для двовибіркового z-тесту.

Приклад: обчислення та інтерпретація значень Z і P

Припустимо, що рівні IQ людей із двох різних міст розподілені нормально, кожен зі стандартним відхиленням населення 15.

Вчений хоче знати, чи відрізняється середній рівень IQ між людьми в містах А та містах Б. Тому вона відбирає просту випадкову вибірку з 20 осіб з кожного міста та записує їхній рівень IQ:

Місто А : 82, 84, 85, 89, 91, 91, 92, 94, 99, 99, 105, 109, 109, 109, 110, 112, 112, 113, 114, 114

Місто Б : 90, 91, 91, 91, 95, 95, 99, 99, 108, 109, 109, 114, 115, 116, 117, 117, 128, 129, 130, 133

Ось як виконати z-тест із двома вибірками, використовуючи ці дані:

Крок 1: Сформулюйте нульову та альтернативну гіпотезу.

Спочатку ми сформулюємо нульову та альтернативну гіпотези:

• H ₀ : μ ₁ = μ ₂ (два середні сукупності рівні)
• H ₁ : μ ₁ ≠ μ ₂ (два середні сукупності не рівні)

Крок 2: обчисліть значення z.

Далі ми виконаємо двовибірковий z-тест в Excel, використовуючи ці дані, і виявимо, що z-значення становить -1,71817 .

Крок 3: обчисліть p-значення.

Ми можемо скористатися калькулятором відношення Z-оцінки до P-значення, щоб знайти, що значення p, яке відповідає значенню az -1,71817, дорівнює 0,08577.

Оскільки це p-значення не менше 0,05, ми не маємо достатніх доказів, щоб відхилити нульову гіпотезу.

Таким чином, ми робимо висновок, що середній рівень IQ суттєво не відрізняється між двома містами.

Зверніть увагу, що ми просто використовували значення z як проміжний крок для обчислення значення p.

P-значення — це справжнє значення, яке нас цікавило, але спочатку нам потрібно було обчислити z-значення.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати z-тести за допомогою різноманітного статистичного програмного забезпечення:

Як виконати Z-тести в Excel
Як виконувати Z-тести в R
Як виконувати Z-тести в Python