Ймовірність vs. пропорція: в чому різниця?

Два терміни, які студенти часто плутають у статистиці, це ймовірність і пропорція .

Ось різниця:

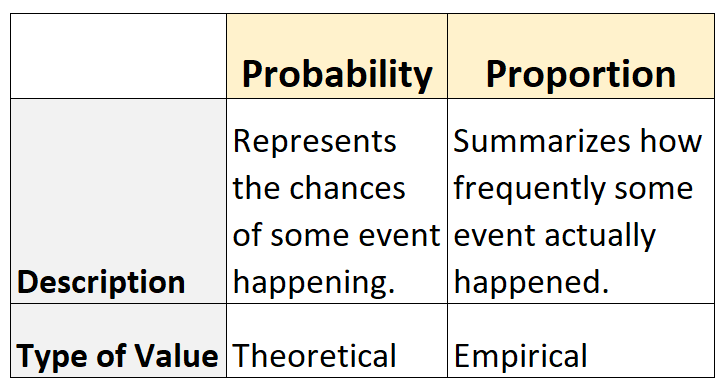
• Імовірність представляє ймовірність події. Це теоретично .
• Пропорція підсумовує, як часто подія насправді відбувалася. Це емпіричне .

Ми часто використовуємо ймовірність, щоб говорити про ймовірність події в майбутньому.

Навпаки, ми часто використовуємо пропорцію, щоб описати, як часто подія насправді відбувалася в минулому.

Наступні приклади ілюструють відмінності між ймовірностями та пропорціями в різних сценаріях.

Приклад 1: ймовірність проти пропорції підкидання монети

Якщо ми кидаємо чесну монету, ймовірність того, що вона випаде орелами, становить 0,5 або 50% .

Однак, якщо ми кидаємо монету 20 разів, ми можемо порахувати, скільки разів вона випадала головами. Наприклад, у 60% випадків, коли він кидає, він може мати голову.

Імовірність того, що монета випаде вгору, є теоретичною, але відсоток випадків, коли монета випаде вгору, є емпіричним – ми могли б порахувати цю частку.

Приклад 2: ймовірність проти пропорції в кидках кубиків

Якщо ви кинете шестигранний кубик, ймовірність того, що він випаде на число «4», становить 1/6 або приблизно 16,67% .

Однак, якщо ми кидаємо кубик 10 разів, ми можемо порахувати, скільки разів він випадав на 4. Наприклад, можливо, він випадав на «4» у 20% кидків.

Імовірність викидання «4» є теоретичною, але частка разів, коли кубик потрапляв на «4», є емпіричною – ми могли б фактично порахувати цю частку.

Приклад 3: ймовірність проти Пропорція в спінерах

Якщо ми обертаємо колесо рулетки, поділене на чотири рівні частини – червону, синю, зелену та фіолетову, – ймовірність того, що воно впаде на фіолетове під час будь-якого обертання, становить 25% .

Однак, якщо ми обертаємо колесо рулетки 100 разів, ми можемо порахувати, скільки разів воно потрапляло на фіолетовий колір. Наприклад, можливо, він потрапив на фіолетовий колір для 15% обертань.

Ймовірність того, що колесо рулетки впаде на фіолетовий колір, є теоретичною, але кількість разів, коли воно впаде на фіолетовий колір, є емпіричною – ми могли б порахувати цю частку.

Приклад 4: Імовірність проти пропорції в карткових іграх

У стандартній колоді з 52 карт є 4 дами. Отже, ймовірність вибору ферзя в розіграші становить 4/52 = 7,69% .

Однак, якщо ми випадково витягнемо (і замінимо взяту карту) 50 разів, ми зможемо підрахувати кількість разів, коли ми витягнемо даму. Наприклад, можливо, ми розіграємо даму в 10% розіграшів.

Ймовірність вибору ферзя є теоретичною, але кількість разів, коли ми фактично вибираємо ферзя, є емпіричною – ми могли б порахувати цю частку.

Додаткові ресурси

Імовірність проти ймовірності: у чому різниця?
Закон повної ймовірності: визначення та приклади