Міжквартильний діапазон (або міжквартильний діапазон)

У цій статті пояснюється, що таке інтерквартильний діапазон, також відомий як інтерквартильний діапазон. Ви також зможете побачити, як обчислюється інтерквартильний діапазон на конкретному прикладі. Ви дізнаєтесь, для чого потрібен інтерквартильний діапазон і різницю з інтервалом. Крім того, ви можете розрахувати інтерквартильний діапазон будь-якого набору даних за допомогою онлайн-калькулятора.

Що таке інтерквартильний (або міжквартильний) діапазон?

Міжквартильний діапазон, також званий інтерквартильним діапазоном, є мірою статистичної дисперсії, яка вказує різницю між третім і першим квартилями. Тому, щоб обчислити інтерквартильний діапазон набору статистичних даних, ви повинні спочатку знайти третій і перший квартилі, а потім відняти їх.

Коротко інтерквартильний діапазон виражається абревіатурою IQR.

Однією з найбільш вигідних характеристик інтерквартильного діапазону є те, що він є надійною статистикою, тобто він має високу надійність до викидів. Оскільки екстремальні значення не враховуються при розрахунку інтерквартильного діапазону, його значення буде дуже мало змінюватися, якщо з’являться нові викиди .

Очевидно, що існують інші міри дисперсії, крім інтерквартильного діапазону, найвідомішими показниками є діапазон, дисперсія, стандартне (або стандартне) відхилення, середнє відхилення та коефіцієнт варіації.

Як розрахувати інтерквартильний (або міжквартильний) діапазон

У статистиці, щоб обчислити міжквартильний діапазон (або інтерквартильний діапазон) набору даних, ви повинні спочатку знайти перший і третій квартилі набору даних, а потім обчислити віднімання третього квартиля мінус перший квартиль.

Таким чином, формула для обчислення інтерквартильного діапазону або інтерквартильного діапазону є:

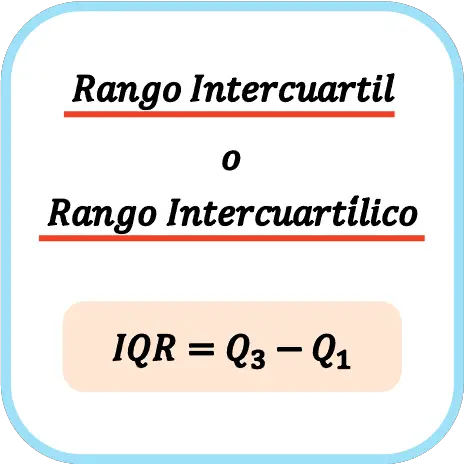
👉 Ви можете скористатися калькулятором нижче, щоб обчислити інтерквартильний діапазон для будь-якого набору даних.

Тому важливо знати, як обчислюються квартилі статистичної вибірки. Ось чому я рекомендую вам, перш ніж продовжити, ознайомитися з наступною статтею, а потім продовжити пояснення.

Приклад інтерквартильного (або міжквартильного) діапазону

Враховуючи визначення та формулу інтерквартильного діапазону (або інтерквартильного діапазону), нижче наведено розв’язану вправу, щоб ви могли точно побачити, як обчислюється цей тип міри дисперсії.

• Ми хочемо статистично проаналізувати, чи доцільно інвестувати в компанію. Для цього ми зібрали дані про вартість акцій цієї компанії за останні 15 місяців. У наведеній нижче таблиці ви можете побачити спостережувані дані в порядку від найнижчого до найвищого. Обчисліть інтерквартильний діапазон для цього набору даних.

Як ми бачили в попередньому розділі, щоб отримати інтерквартильний діапазон (або інтерквартильний діапазон) вибірки, ми повинні спочатку обчислити перший і третій квартилі.

Перший квартиль є медіаною першої половини значень, що відповідає 8,95 євро/акцію.

З іншого боку, третій квартиль є проміжним значенням другої половини значень, тому він становить 9,83 євро/акцію.

Отже, щоб знайти інтерквартильний діапазон, просто застосуйте формулу та відніміть третій квартиль мінус перший квартиль.

Калькулятор міжквартильного (або міжквартильного) діапазону

Введіть набір статистичних даних у наведений нижче калькулятор, щоб обчислити його інтерквартильний діапазон або інтерквартильний діапазон. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Різниця між інтерквартильним діапазоном і діапазоном

У статистиці різниця між інтерквартильним діапазоном (або міжквартильним діапазоном) і інтервалом – це значення, які беруться для виконання розрахунку. Інтерквартильний діапазон – це різниця між третім і першим квартилем, а діапазон – це різниця між крайніми значеннями вибірки.

Таким чином, інтерквартильний діапазон вимірює дисперсію вибірки з використанням центральних даних, тоді як інтервал кількісно визначає дисперсію вибірки з використанням екстремальних даних.

Тому на статистичний діапазон набагато більше впливають викиди , оскільки вони зазвичай являють собою мінімум або максимум набору даних. Таким чином, одна з переваг інтерквартильного діапазону над інтервалом полягає в тому, що він має більшу стійкість.

Для чого використовується інтерквартильний (або міжквартильний) діапазон?

Насамперед інтерквартильний діапазон (або інтерквартильний діапазон) використовується для вимірювання розподілу набору даних . Хоча аналіз дисперсії вибірки вимагає обчислення більшої кількості статистичних показників, інтерквартильний діапазон дає уявлення про те, наскільки дисперсна вибірка, принаймні центральні значення.

Тому інтерпретація інтерквартильного діапазону відносно проста. Чим вище значення інтерквартильного діапазону, тим більше розсіяні середні дані у вибірці, і чим менший інтерквартильний діапазон, тим ближче один до одного середні дані.

Крім того, інтерквартильний діапазон також корисний для створення діаграми коробки та вуса, широко використовуваної діаграми для аналізу поведінки ціни акцій на фондовому ринку.