Як виконати односторонній дисперсійний аналіз на калькуляторі ti-84

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

У цьому посібнику пояснюється, як виконати односторонній дисперсійний аналіз на калькуляторі TI-84.

Приклад: односторонній дисперсійний аналіз на калькуляторі TI-84

Припустимо, ми набираємо 30 студентів для участі в дослідженні. Студентів випадковим чином розподіляють на використання однієї з трьох методів навчання протягом місяця для підготовки до іспиту. Наприкінці місяця всі учні складають один і той же тест.

Виконайте наступні дії, щоб виконати односторонній дисперсійний аналіз, щоб визначити, чи однакові середні бали в трьох групах.

Крок 1: Введіть дані.

Спочатку ми введемо значення даних для пояснювальної змінної та змінної відповіді. Натисніть Stat, потім натисніть EDIT . Введіть наведені нижче результати іспиту для студентів, які використовували першу методику навчання в колонку L1, другу методику навчання в колонку L2 і третю методику навчання в колонку L3:

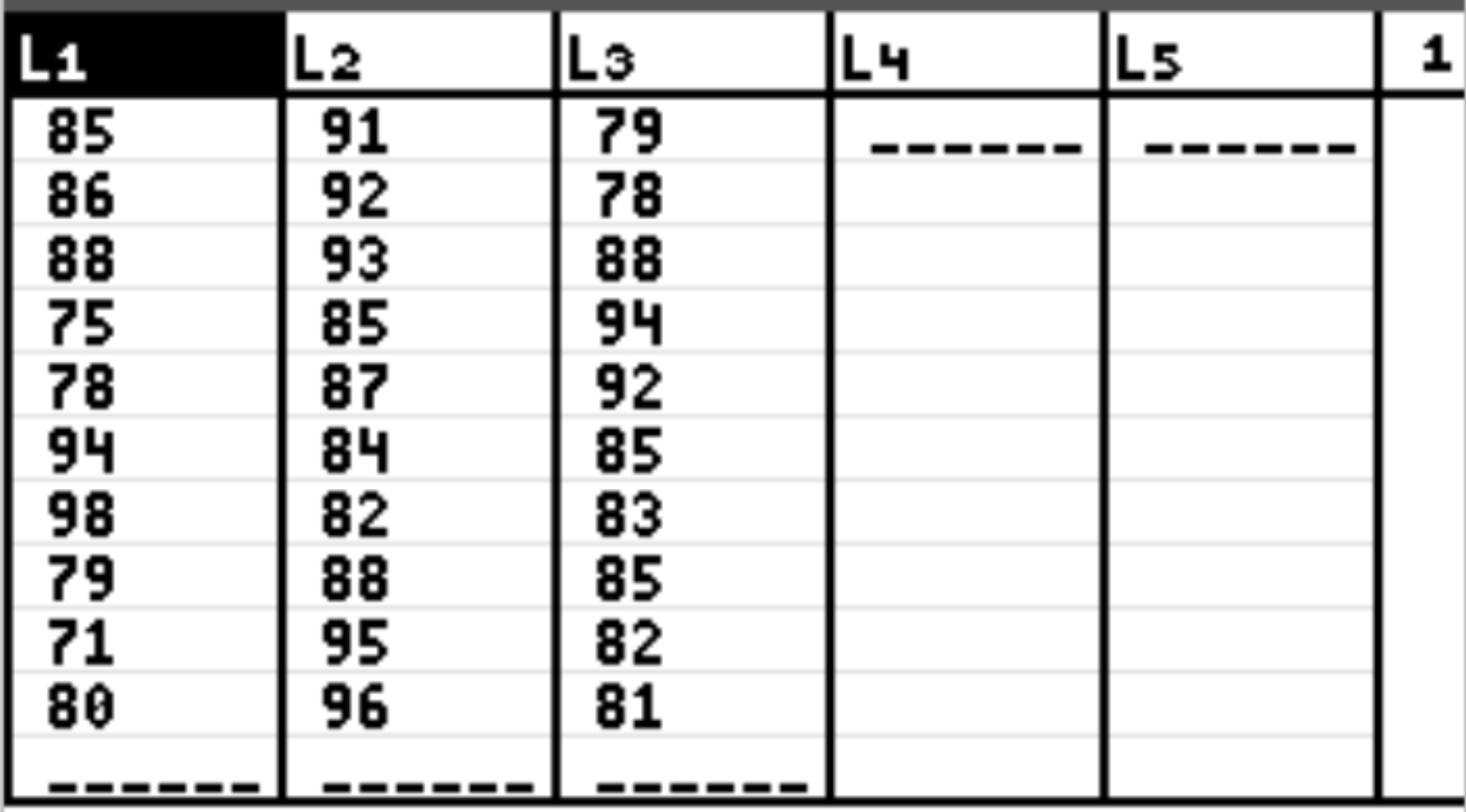
Крок 2: Виконайте односторонній дисперсійний аналіз.

Далі ми виконаємо односторонній дисперсійний аналіз. Натисніть Stat, а потім перейдіть до TESTS . Потім прокрутіть униз до ANOVA та натисніть Enter .

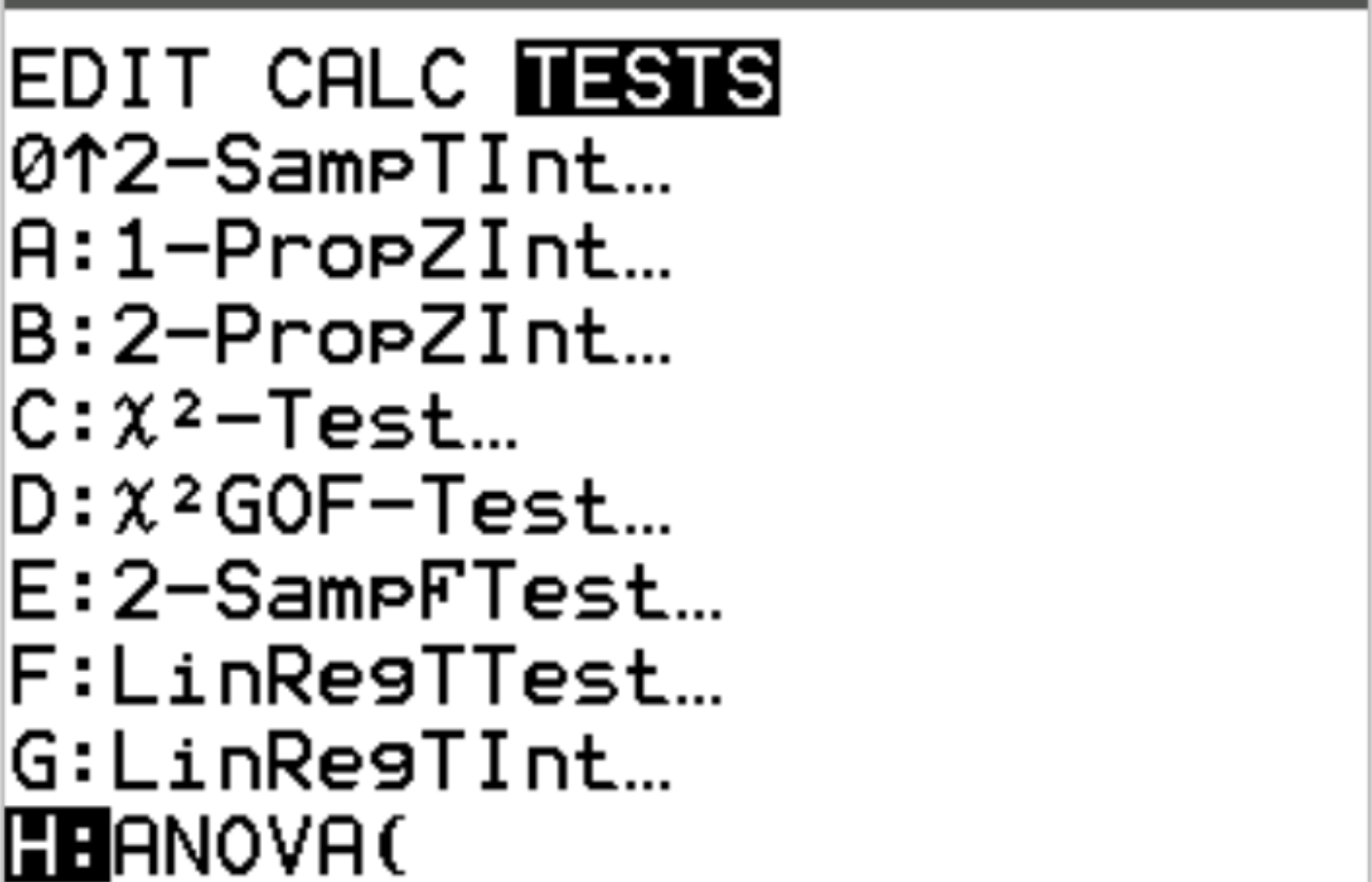
Введіть списки, у яких зберігаються дані, розділивши їх комами, потім додайте закриваючу дужку ) , а потім натисніть Enter .

Примітка. Щоб відобразити L1, натисніть 2 , потім натисніть 1 . Щоб викликати L2, натисніть 2nd, а потім натисніть 2 . Щоб відкрити L3, натисніть 2nd, а потім натисніть 3 .

Після натискання клавіші Enter з’являться такі результати:

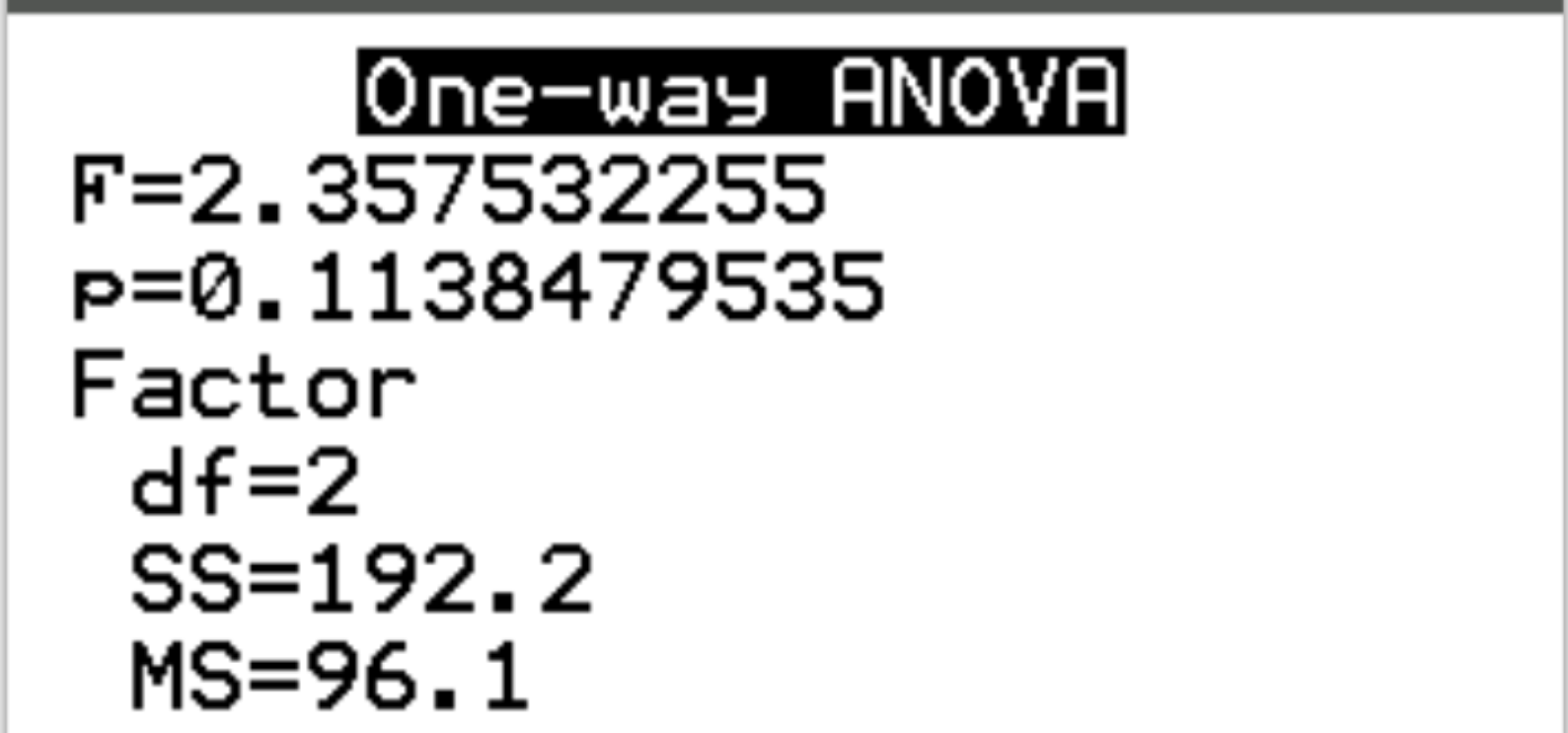
Крок 3: Інтерпретація результатів.

F-статистика тесту становить 2,3575 , а відповідне значення p — 0,1138 . Оскільки це p-значення не менше 0,05, ми не можемо відхилити нульову гіпотезу.

Таким чином, ми не маємо достатніх доказів, щоб стверджувати, що середній бал за іспит у трьох групах відрізняється. Іншими словами, ми не маємо достатньо доказів, щоб стверджувати, що методика дослідження призводить до різних результатів тестування.