Як обчислити біноміальні ймовірності на калькуляторі ti-84
Біноміальний розподіл є одним із найбільш часто використовуваних розподілів у всій статистиці. У цьому підручнику пояснюється, як використовувати такі функції на калькуляторі TI-84 для знаходження біноміальних ймовірностей:
binompdf(n, p, x) повертає ймовірність, пов’язану з біноміальним pdf.
binomcdf(n, p, x) повертає кумулятивну ймовірність, пов’язану з біномом cdf.
золото:
- n = кількість випробувань
- p = ймовірність успіху в даному випробуванні
- x = загальна кількість успіхів
Ці дві функції доступні на калькуляторі TI-84, натиснувши 2nd, а потім натиснувши vars . Це приведе вас до екрана DISTR , де ви зможете використовувати binompdf() і binomcdf() :
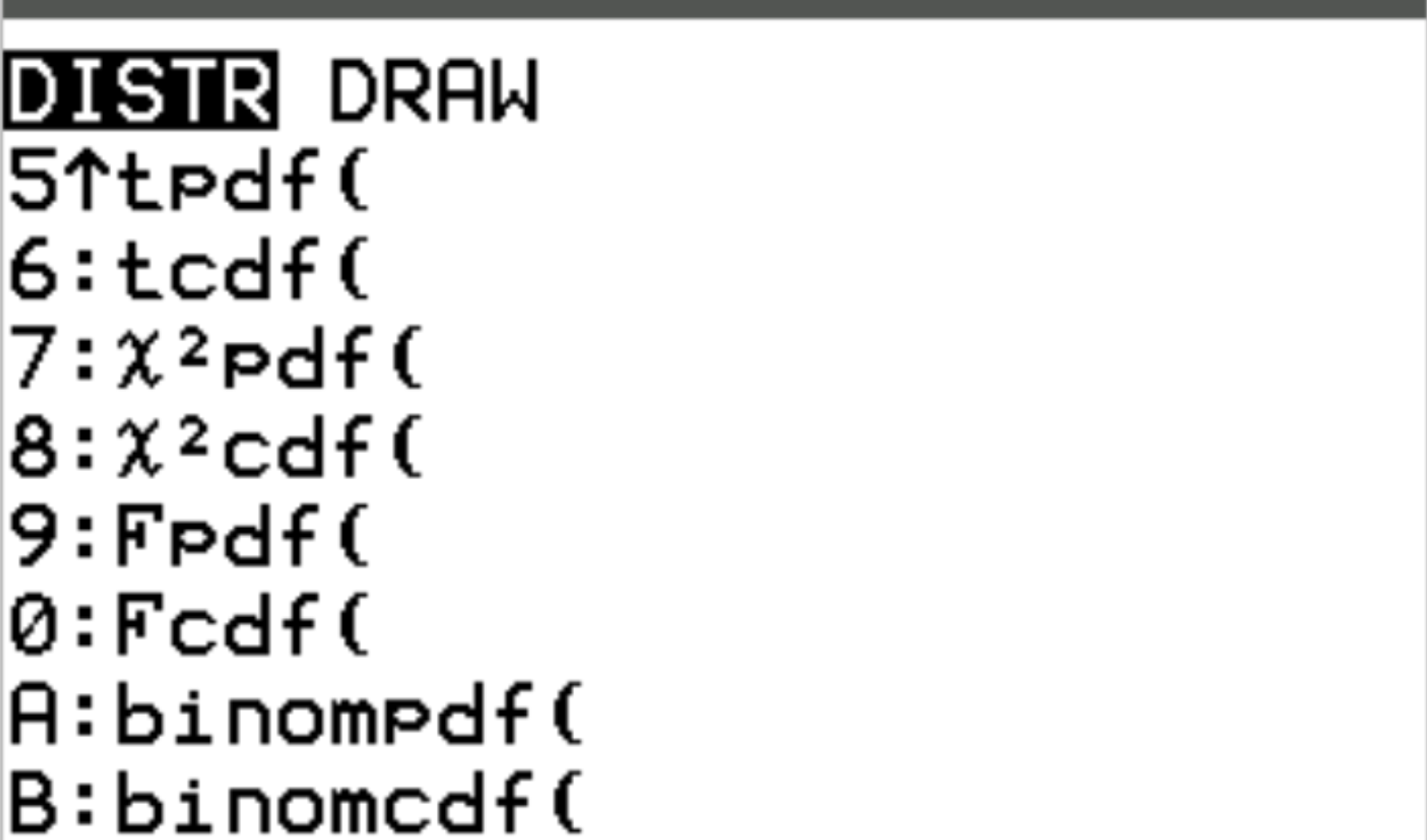
Наступні приклади ілюструють, як використовувати ці функції для відповідей на різні запитання.
Приклад 1: біноміальна ймовірність успіху рівно x
Запитання: Натан виконує 60% своїх спроб зі штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить рівно 10?
Відповідь: Використовуйте функцію binomialpdf(n, p, x):
біном PDF(12, .60, 10) = 0,0639
Приклад 2: біноміальна ймовірність успіху менше х
Запитання: Натан виконує 60% своїх спроб зі штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить менше 10?
Відповідь: Використовуйте функцію binomialcdf(n, p, x-1) :
біном cdf(12, .60, 9) = 0,9166
Приклад 3: біноміальна ймовірність не більше x успіху
Запитання: Натан виконує 60% своїх спроб зі штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить не більше 10?
Відповідь: Використовуйте функцію binomialcdf(n, p, x) :
біном cdf(12, .60, 10) = 0,9804
Приклад 4: Біноміальна ймовірність більш ніж x успіхів
Запитання: Натан виконує 60% своїх спроб зі штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить більше 10?
Відповідь: Використовуйте функцію 1 – binomialcdf(n, p, x) :
1 – біном cdf(12, .60, 10) = 0,0196
Приклад 5: біноміальна ймовірність принаймні x успіху
Запитання: Натан виконує 60% своїх спроб зі штрафних кидків. Якщо він виконує 12 штрафних кидків, яка ймовірність того, що він зробить більше 10?
Відповідь: Використовуйте функцію 1 – binomialcdf(n, p, x-1) :
1 – біном cdf(12, .60, 9) = 0,0834