Як виконати лінійну регресію на калькуляторі ti-84

Лінійна регресія — це метод, який ми можемо використовувати для розуміння зв’язку між пояснювальною змінною x і змінною відповіді y.

У цьому посібнику пояснюється, як виконувати лінійну регресію на калькуляторі TI-84.

Приклад: лінійна регресія на калькуляторі TI-84

Припустімо, ми хочемо зрозуміти залежність між кількістю годин, які студент готує до іспиту, та оцінкою, яку він отримує на іспиті.

Щоб дослідити цей зв’язок, ми можемо виконати наступні кроки на калькуляторі TI-84, щоб виконати просту лінійну регресію, використовуючи вивчені години як пояснювальну змінну та оцінку іспиту як змінну відповіді.

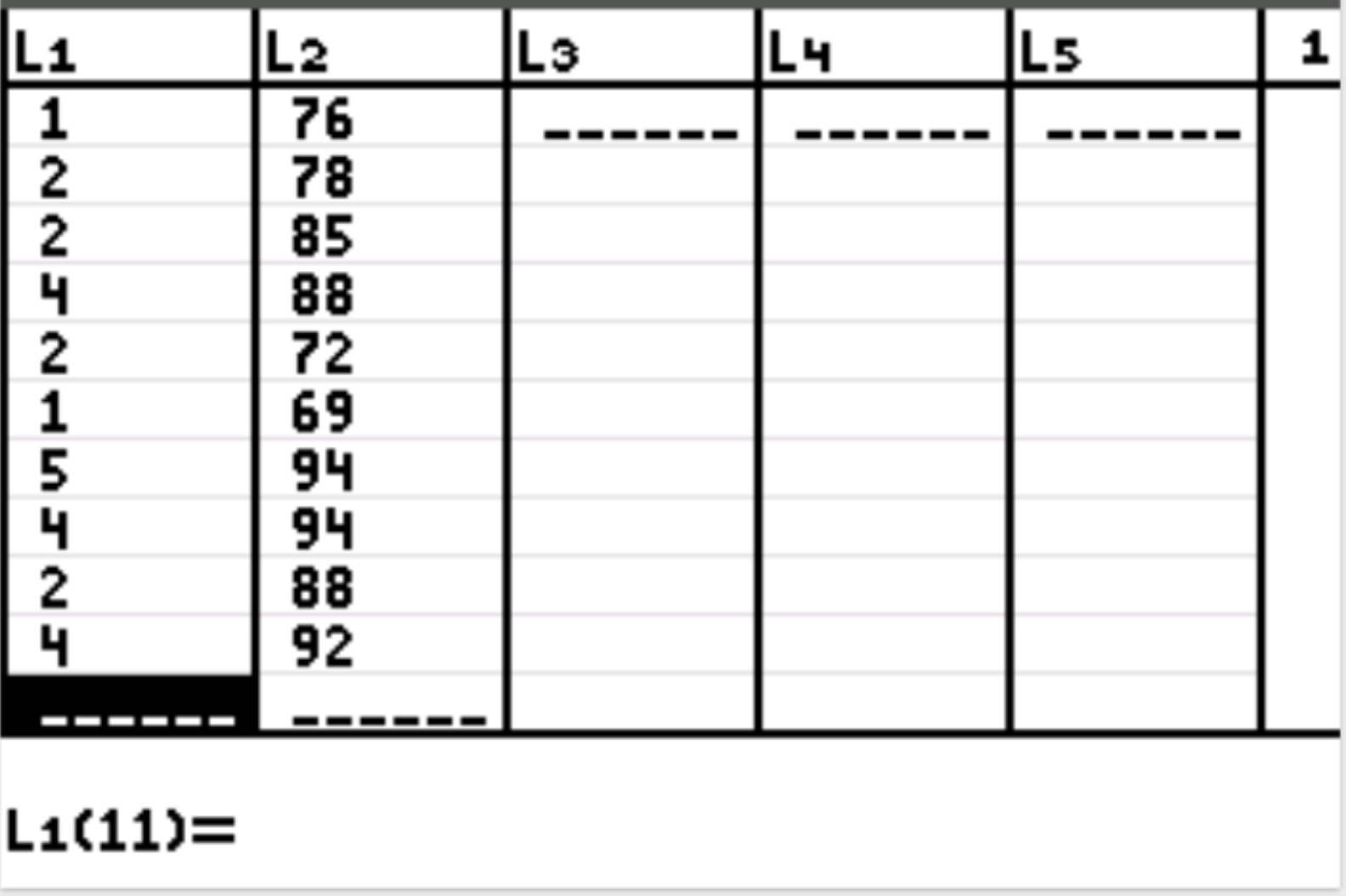
Крок 1: Введіть дані.

Спочатку ми введемо значення даних для пояснювальної змінної та змінної відповіді. Натисніть Stat, потім натисніть EDIT . Введіть наступні значення для пояснювальної змінної (вивчені години) у стовпець L1 і значення для змінної відповіді (екзаменаційний бал) у стовпець L2:

Крок 2: Виконайте лінійну регресію.

Далі ми виконаємо лінійну регресію. Натисніть Stat, а потім перейдіть до CALC . Потім прокрутіть до 8: Linreg(a+bx) і натисніть Enter .

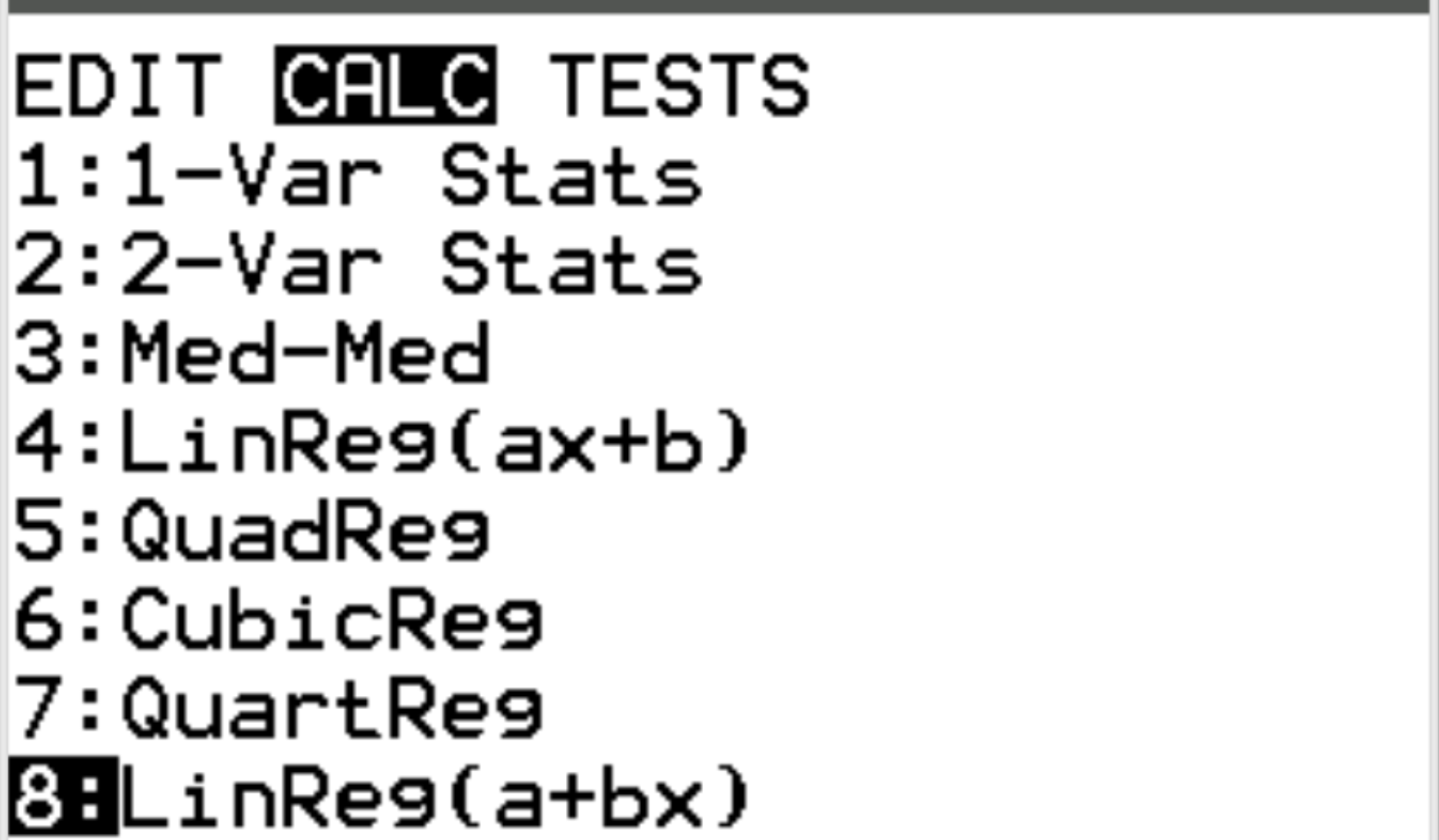
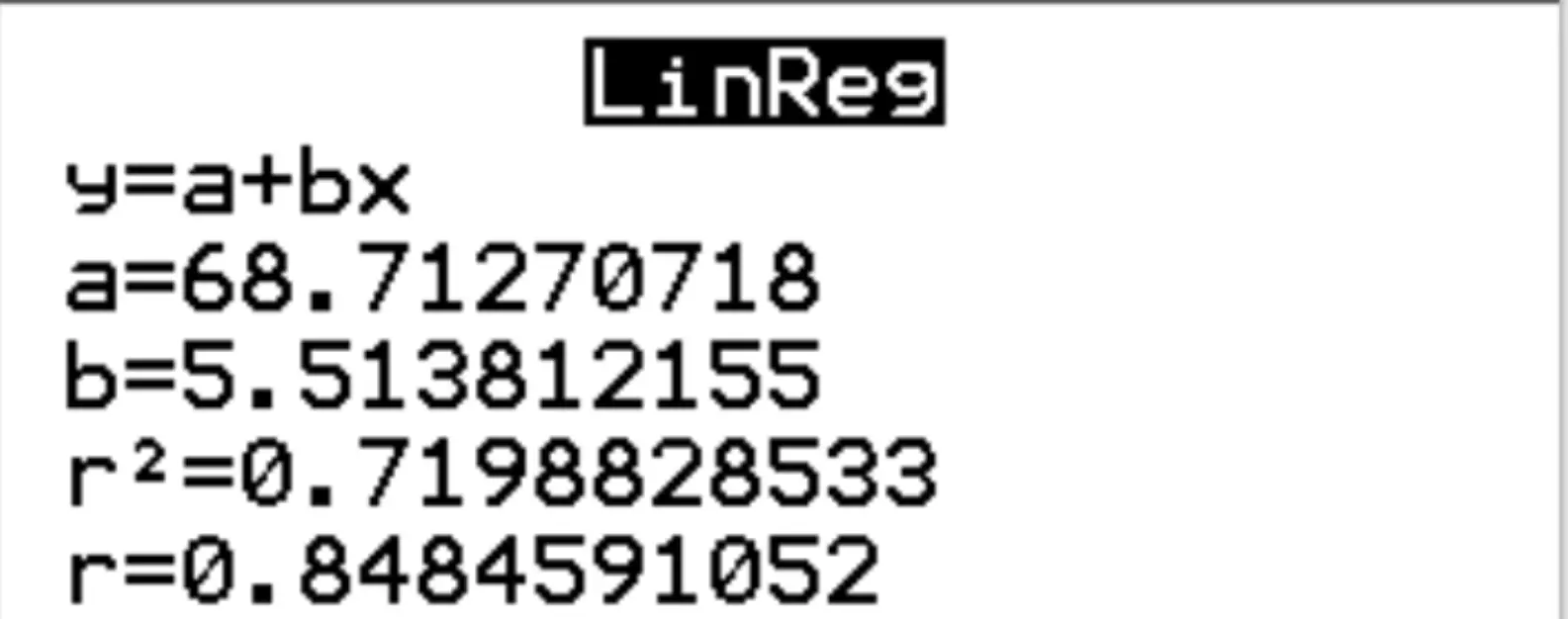
Для Xlist і Ylist переконайтеся, що вибрано L1 і L2, оскільки це стовпці, які ми використовували для введення наших даних. Залиште FreqList порожнім. Прокрутіть униз до пункту «Обчислити» та натисніть «Enter» . Автоматично з’явиться такий результат:

Крок 3: Інтерпретація результатів.

З результатів ми бачимо, що оцінене рівняння регресії таке:

оцінка за іспит = 68,7127 + 5,5138*(години)

Ми тлумачимо коефіцієнт годин так, що за кожну додаткову вивчену годину оцінка іспиту має зрости в середньому на 5,5138 . Ми інтерпретуємо коефіцієнт перетину так, що очікуваний іспитовий бал для студента, який вивчає нуль годин, становить 68,7127 .

Ми можемо використовувати це оцінене рівняння регресії, щоб обчислити очікуваний іспитовий бал для студента на основі кількості годин навчання.

Наприклад, студент, який навчається протягом трьох годин, повинен отримати іспитовий бал 85,25 :

бал = 68,7127 + 5,5138*(3) = 85,25

Ми також бачимо, що r у квадраті для регресійної моделі становить r ² = 0,7199 .

Ця величина відома як коефіцієнт детермінації. Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі 71,99% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.

Додаткові ресурси

Як створити графік залишків на калькуляторі TI-84
Як виконати квадратичну регресію на калькуляторі TI-84
Як виконати експоненціальну регресію на калькуляторі TI-84
Як виконати логарифмічну регресію на калькуляторі TI-84