Як обчислити нормальні ймовірності на калькуляторі ti-84
Нормальний розподіл є найбільш часто використовуваним розподілом у всій статистиці. У цьому підручнику пояснюється, як використовувати такі функції на калькуляторі TI-84 для знаходження ймовірностей нормального розподілу:
normalpdf(x, μ, σ) повертає ймовірність, пов’язану зі звичайним pdf, де:
- x = індивідуальне значення
- μ = середнє значення популяції
- σ = стандартне відхилення сукупності
normalcdf(lower_x, upper_x, μ, σ) повертає кумулятивну ймовірність, пов’язану з нормальним cdf між двома значеннями.
золото:
- lower_x = нижче індивідуальне значення
- upper_x = верхнє індивідуальне значення
- μ = середнє значення популяції
- σ = стандартне відхилення сукупності
Ці дві функції доступні на калькуляторі TI-84, натиснувши 2nd, а потім натиснувши vars . Це приведе вас до екрана DISTR , де ви зможете використовувати normalpdf() і normalcdf() :
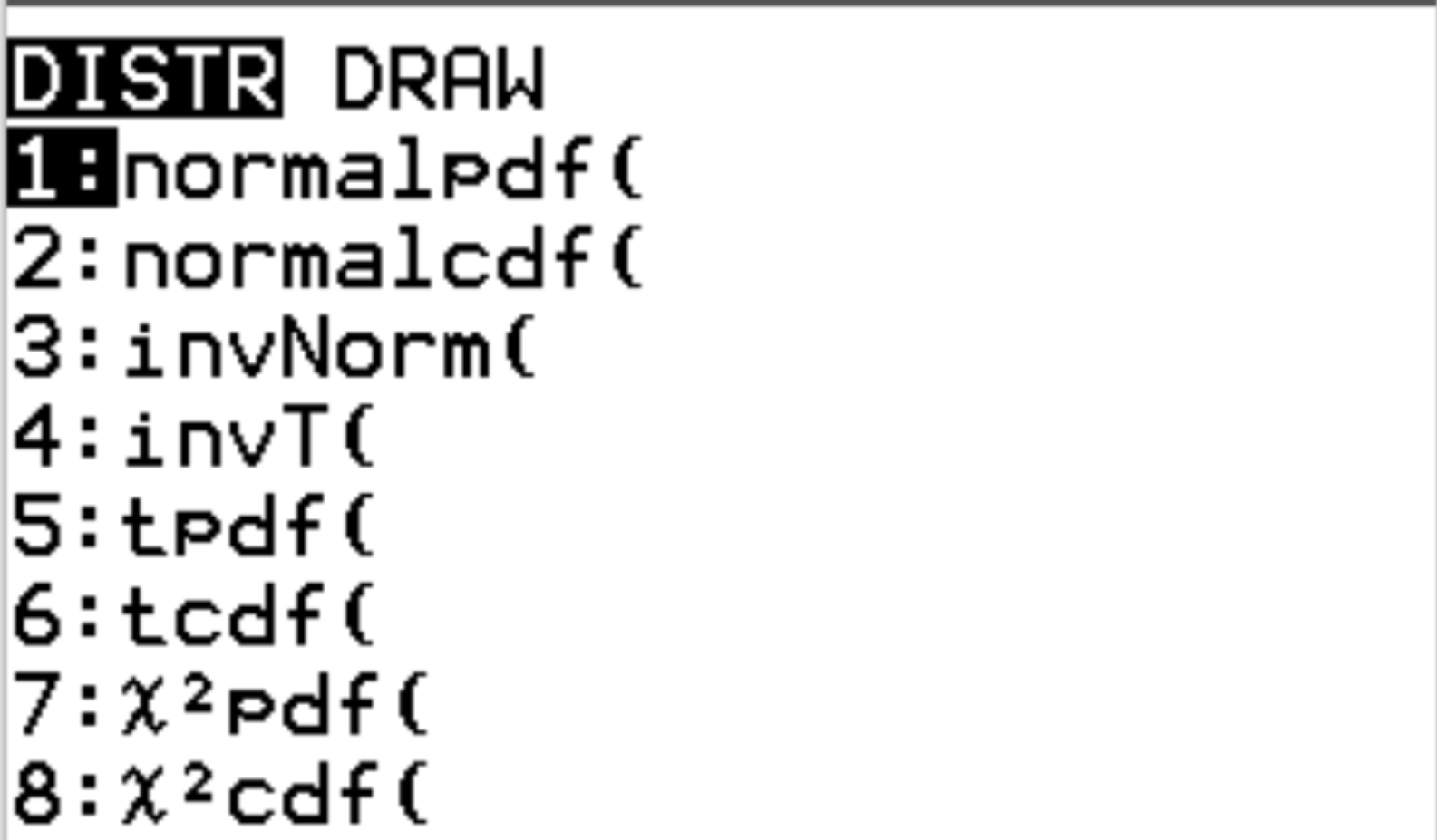
Наступні приклади ілюструють, як використовувати ці функції для відповідей на різні запитання.
Приклад 1: нормальна ймовірність більша за x
Запитання: для нормального розподілу із середнім значенням = 40 і стандартним відхиленням = 6 знайдіть імовірність того, що значення перевищує 45.
Відповідь: скористайтеся функцією normalcdf(x, 10000, μ, σ):
normalcdf(45, 10000, 40, 6) = 0,2023
Примітка. Оскільки функція вимагає значення upper_x, ми просто використовуємо 10 000.
Приклад 2: нормальна ймовірність менше х
Запитання: для нормального розподілу із середнім значенням = 100 і стандартним відхиленням = 11,3 знайдіть імовірність того, що значення менше 98.
Відповідь: скористайтеся функцією normalcdf(-10000, x, μ, σ):
normalcdf(-10000, 98, 100, 11,3) = 0,4298
Примітка. Оскільки для функції потрібне нижче значення_x, ми просто використовуємо -10000.
Приклад 3: Нормальна ймовірність між двома значеннями
Запитання: для нормального розподілу із середнім значенням = 50 і стандартним відхиленням = 4 знайдіть імовірність того, що значення буде між 48 і 52.
Відповідь: Використовуйте функцію normalcdf(smaller_x, Larger_x, μ, σ)
normalcdf(48, 52, 50, 4) = 0,3829
Приклад 4: Нормальна ймовірність за винятком двох значень
Запитання: для нормального розподілу із середнім = 22 і стандартним відхиленням = 4 знайдіть імовірність того, що значення менше 20 або більше 24.
Відповідь: Використовуйте функцію normalcdf(-10000, small_x, μ, σ) + normalcdf(larger_x, 10000, μ, σ)
normalcdf(-10000, 20, 22, 4) + normalcdf(24, 10000, 22, 4) = 0,6171