Як виконати квадратичну регресію в python

Квадратична регресія – це тип регресії, який ми можемо використати для кількісного визначення зв’язку між змінною прогнозу та змінною відповіді, коли справжні зв’язки є квадратичними, що може виглядати як «U» або перевернуте «U» на графіку.

Тобто, коли змінна предиктора збільшується, змінна відповіді також має тенденцію до збільшення, але після певного моменту змінна відповіді починає зменшуватися, оскільки змінна предиктора продовжує зростати.

Цей підручник пояснює, як виконати квадратичну регресію в Python.

Приклад: квадратична регресія в Python

Припустімо, що у нас є дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 16 різних людей:

 import numpy as np
import scipy.stats as stats

#define variables
hours = [6, 9, 12, 12, 15, 21, 24, 24, 27, 30, 36, 39, 45, 48, 57, 60]
happ = [12, 18, 30, 42, 48, 78, 90, 96, 96, 90, 84, 78, 66, 54, 36, 24]

Якщо ми побудуємо просту точкову діаграму цих даних, ми побачимо, що зв’язок між двома змінними має форму «U»:

 import matplotlib.pyplot as plt

#create scatterplot
plt.scatter(hours, happ) 

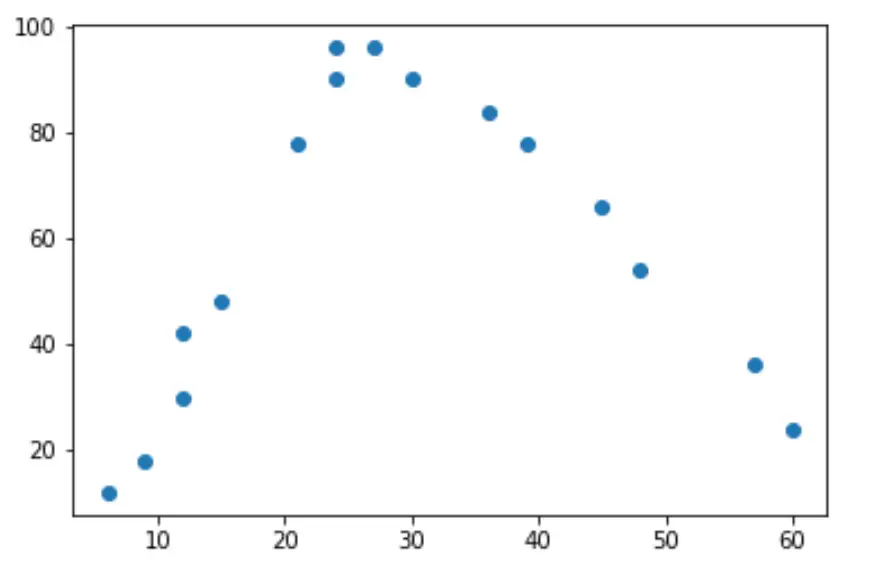
Зі збільшенням кількості відпрацьованих годин підвищується і щастя, але як тільки відпрацьовані години перевищують приблизно 35 годин на тиждень, щастя починає падати.

Через цю форму «U» це означає, що квадратична регресія, ймовірно, є хорошим кандидатом для кількісного визначення зв’язку між двома змінними.

Щоб фактично виконати квадратичну регресію, ми можемо підібрати модель поліноміальної регресії зі ступенем 2 за допомогою функції numpy.polyfit() :

 import numpy as np

#polynomial fit with degree = 2
model = np.poly1d(np.polyfit(hours, happ, 2))

#add fitted polynomial line to scatterplot
polyline = np.linspace(1, 60, 50)
plt.scatter(hours, happ)
plt.plot(polyline, model(polyline))
plt.show() 

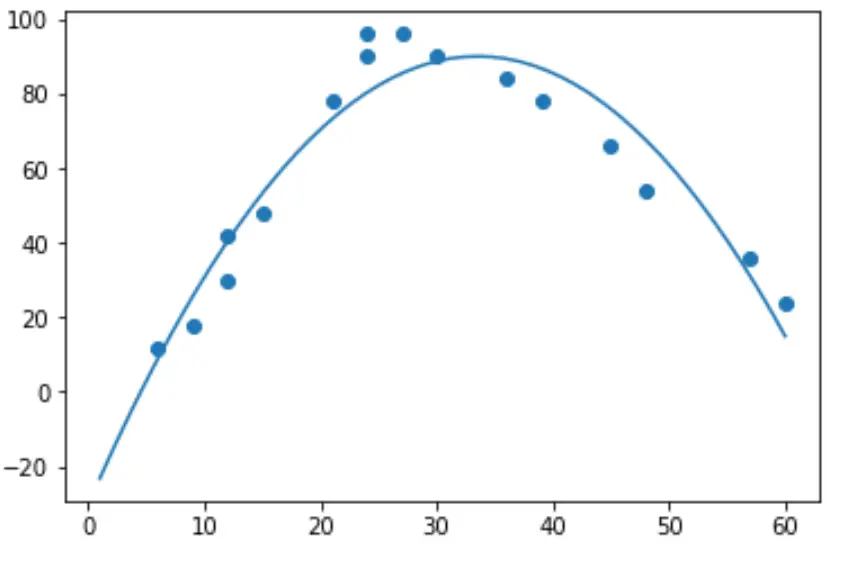
Ми можемо отримати підігнане поліноміальне рівняння регресії, надрукувавши коефіцієнти моделі:

 print (model)

-0.107x 2 + 7.173x - 30.25

Зібране рівняння квадратної регресії має вигляд:

Щастя = -0,107 (годин) ² + 7,173 (годин) – 30,25

Ми можемо використовувати це рівняння, щоб обчислити очікуваний рівень щастя людини на основі відпрацьованих годин. Наприклад, очікуваний рівень щастя людини, яка працює 30 годин на тиждень:

Щастя = -0,107(30) ² + 7,173(30) – 30,25 = 88,64 .

Ми також можемо написати коротку функцію, щоб отримати R-квадрат моделі, який є часткою дисперсії у змінній відповіді, яку можна пояснити змінними предиктора.

 #define function to calculate r-squared
def polyfit(x, y, degree):
    results = {}
    coeffs = np.polyfit(x, y, degree)
    p = np.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat-ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#find r-squared of polynomial model with degree = 3
polyfit(hours, happ, 2)

{'r_squared': 0.9092114182131691}

У цьому прикладі R-квадрат моделі становить 0,9092 .

Це означає, що 90,92% варіацій у зареєстрованих рівнях щастя можна пояснити змінними-прогностиками.

Додаткові ресурси

Як виконати поліноміальну регресію в Python
Як виконати квадратичну регресію в R
Як виконати квадратичну регресію в Excel