Як виконати квадратичну регресію в r

Коли дві змінні мають лінійний зв’язок, ми часто можемо використовувати просту лінійну регресію , щоб кількісно визначити їхній зв’язок.

Однак, коли дві змінні мають квадратичний зв’язок, ми можемо використати квадратичну регресію , щоб кількісно визначити їхній зв’язок.

У цьому посібнику пояснюється, як виконати квадратичну регресію в R.

Приклад: квадратична регресія в R

Припустімо, ми хочемо зрозуміти зв’язок між кількістю відпрацьованих годин і заявленим щастям. У нас є такі дані про кількість відпрацьованих годин на тиждень і рівень щастя (за шкалою від 0 до 100) для 11 різних людей:

Виконайте наступні кроки, щоб підібрати модель квадратичної регресії в R.

Крок 1: Введіть дані.

Спочатку ми створимо фрейм даних, що містить наші дані:

 #createdata
data <- data.frame(hours=c(6, 9, 12, 14, 30, 35, 40, 47, 51, 55, 60),
                   happiness=c(14, 28, 50, 70, 89, 94, 90, 75, 59, 44, 27))

#viewdata 
data

   hours happiness
1 6 14
2 9 28
3 12 50
4 14 70
5 30 89
6 35 94
7 40 90
8 47 75
9 51 59
10 55 44
11 60 27

Крок 2: Візуалізуйте дані.

Далі ми створимо просту діаграму розсіювання для візуалізації даних.

 #create scatterplot
plot(data$hours, data$happiness, pch=16) 

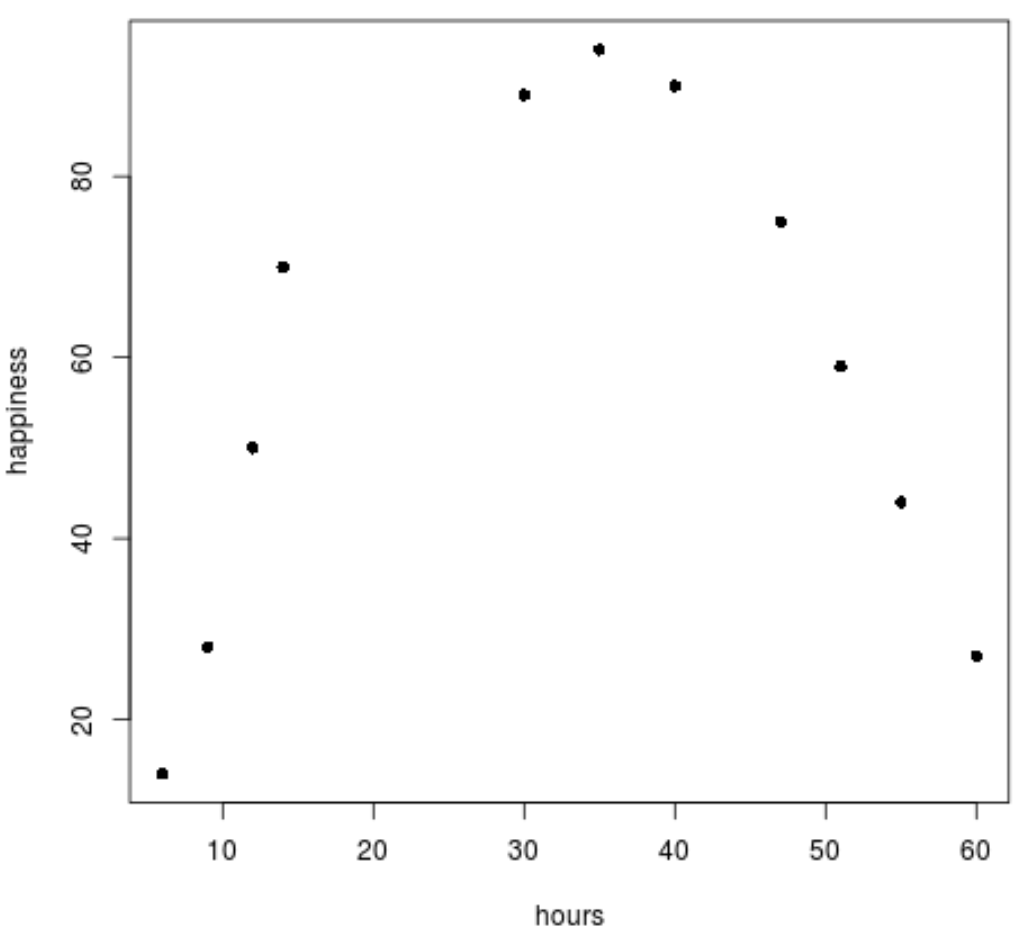
Ми чітко бачимо, що дані не дотримуються лінійної моделі.

Крок 3. Підберіть просту модель лінійної регресії.

Далі ми підберемо просту модель лінійної регресії, щоб побачити, наскільки добре вона відповідає даним:

 #fit linear model
linearModel <- lm(happiness ~ hours, data=data)

#view model summary
summary(linearModel)

Call:
lm(formula = happiness ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-39.34 -21.99 -2.03 23.50 35.11 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) 48.4531 17.3288 2.796 0.0208 *
hours 0.2981 0.4599 0.648 0.5331  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 28.72 on 9 degrees of freedom
Multiple R-squared: 0.0446, Adjusted R-squared: -0.06156 
F-statistic: 0.4201 on 1 and 9 DF, p-value: 0.5331

Загальна дисперсія рівня щастя, пояснена моделлю, становить лише 4,46% , як показує кратне значення R-квадрат.

Крок 4. Підберіть модель квадратичної регресії.

Далі ми підберемо модель квадратичної регресії.

 #create a new variable for hours 2
data$hours2 <- data$hours^2

#fit quadratic regression model
quadraticModel <- lm(happiness ~ hours + hours2, data=data)

#view model summary
summary(quadraticModel)

Call:
lm(formula = happiness ~ hours + hours2, data = data)

Residuals:
    Min 1Q Median 3Q Max 
-6.2484 -3.7429 -0.1812 1.1464 13.6678 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 6.218 on 8 degrees of freedom
Multiple R-squared: 0.9602, Adjusted R-squared: 0.9502 
F-statistic: 96.49 on 2 and 8 DF, p-value: 2.51e-06

Загальна дисперсія рівня щастя, пояснена моделлю, зросла до 96,02% .

Ми можемо використати наступний код, щоб візуалізувати, наскільки добре модель відповідає даним:

 #create sequence of hour values
hourValues <- seq(0, 60, 0.1)

#create list of predicted happiness levels using quadratic model
happinessPredict <- predict(quadraticModel, list(hours=hourValues, hours2=hourValues^2))

#create scatterplot of original data values
plot(data$hours, data$happiness, pch=16)
#add predicted lines based on quadratic regression model
lines(hourValues, happinessPredict, col='blue')

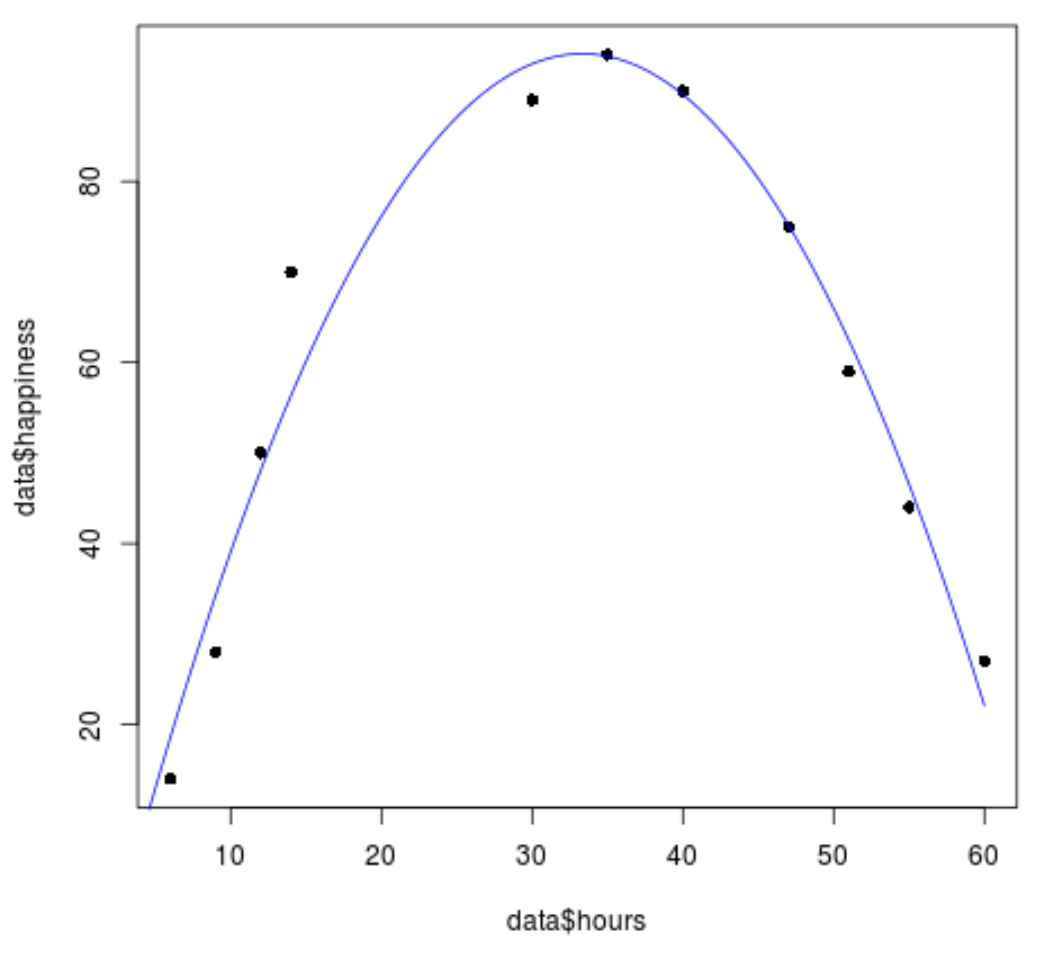
Ми бачимо, що лінія квадратичної регресії досить добре відповідає значенням даних.

Крок 5: Інтерпретація моделі квадратичної регресії.

На попередньому кроці ми побачили, що результат моделі квадратичної регресії:

 Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -18.25364 6.18507 -2.951 0.0184 *  
hours 6.74436 0.48551 13.891 6.98e-07 ***
hours2 -0.10120 0.00746 -13.565 8.38e-07 ***

На основі наведених тут коефіцієнтів скоригована квадратична регресія буде:

Щастя = -0,1012 (годин) ² + 6,7444 (годин) – 18,2536

Ми можемо використовувати це рівняння, щоб знайти прогнозоване щастя людини, враховуючи кількість годин, які вони працюють на тиждень.

Наприклад, людина, яка працює 60 годин на тиждень, матиме рівень щастя 22,09 :

Щастя = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

І навпаки, людина, яка працює 30 годин на тиждень, повинна мати рівень щастя 92,99 :

Щастя = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99