Як виконати квантильну регресію в r

Лінійна регресія – це метод, який ми можемо використати для розуміння зв’язку між однією або декількома змінними предиктора та змінною відповіді .

Як правило, коли ми виконуємо лінійну регресію, ми хочемо оцінити середнє значення змінної відповіді.

Однак замість цього ми могли б використати метод, відомий як квантильна регресія , щоб оцінити будь-яке значення квантиля або процентиля значення відповіді, наприклад 70-й процентиль, 90-й процентиль, 98-й процентиль тощо.

Щоб виконати квантильну регресію в R, ми можемо використати функцію rq() із пакета quantreg , яка використовує такий синтаксис:

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

золото:

• y: змінна відповіді
• x: передбачувана змінна(и)
• дані: назва набору даних
• tau: процентиль, який потрібно знайти. Типовим значенням є медіана (tau = 0,5), але ви можете встановити будь-яке число від 0 до 1.

Цей підручник надає покроковий приклад того, як використовувати цю функцію для виконання квантильної регресії в R.

Крок 1: Введіть дані

Для цього прикладу ми створимо набір даних, який міститиме вивчені години та результати іспитів, отримані для 100 різних студентів університету:

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

Крок 2: Виконайте квантильну регресію

Далі ми підіб’ємо модель квантильної регресії, використовуючи вивчені години як змінну прогностику та оцінки за іспит як змінну відповіді.

Ми використаємо цю модель, щоб передбачити очікуваний 90-й процентиль іспитових балів на основі кількості вивчених годин:

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

З результату ми можемо побачити оцінене рівняння регресії:

90-й процентиль іспиту = 60,25 + 2,437*(години)

Наприклад, 90-й процентиль для всіх студентів, які навчаються 8 годин, має становити 79,75:

90-й процентиль оцінки за іспит = 60,25 + 2,437*(8) = 79,75 .

Вихідні дані також відображають верхню та нижню межі достовірності для перехоплення та часів змінної предиктора.

Крок 3: Візуалізуйте результати

Ми також можемо візуалізувати результати регресії, створивши діаграму розсіювання з підігнаним квантильним рівнянням регресії, накладеним на графік:

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

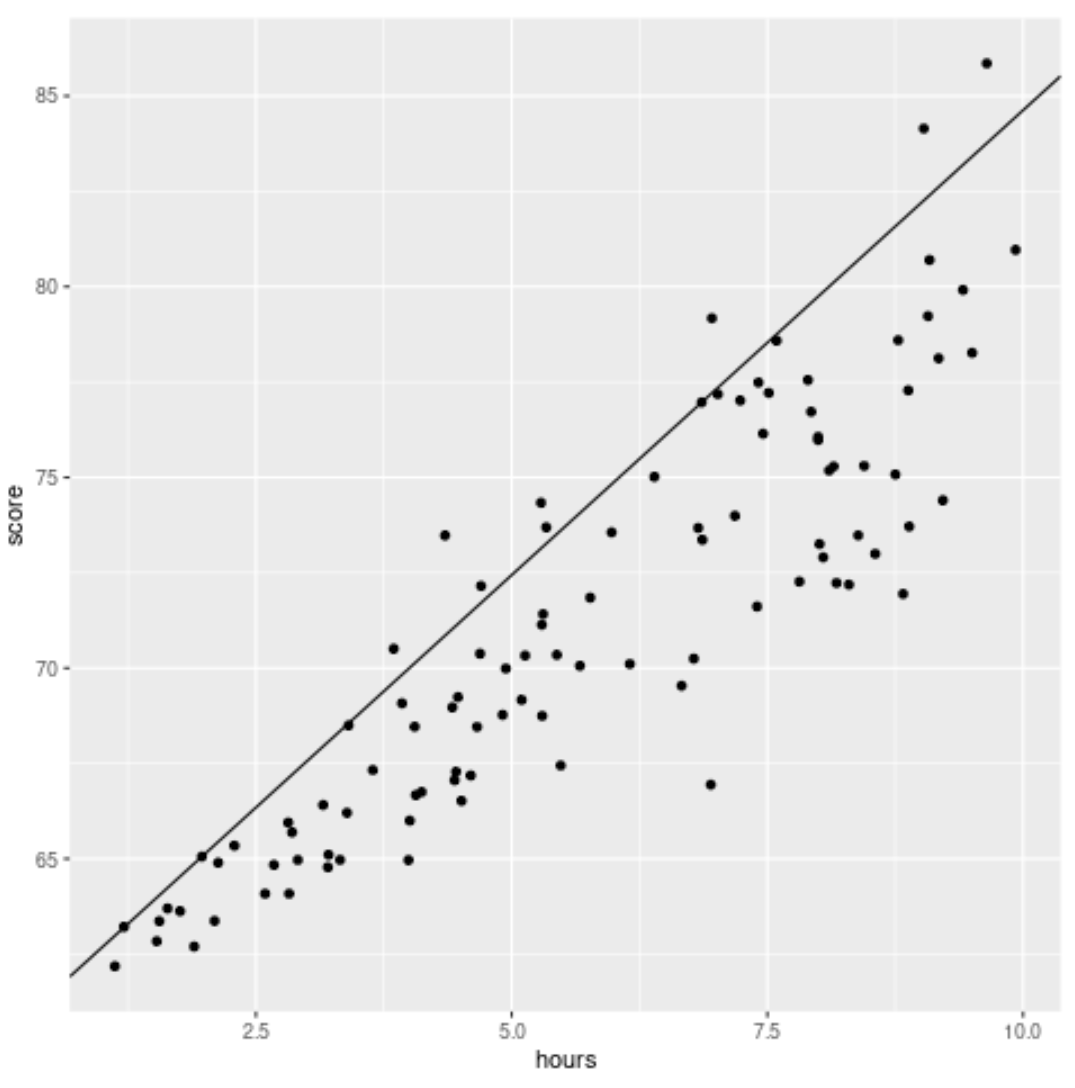
На відміну від традиційної лінії лінійної регресії, зауважте, що ця підібрана лінія не проходить через серцевину даних. Натомість він проходить через розрахунковий 90-й процентиль на кожному рівні змінної предиктора.

Ми можемо побачити різницю між підігнаним рівнянням квантильної регресії та простим рівнянням лінійної регресії, додавши аргумент geom_smooth() :

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

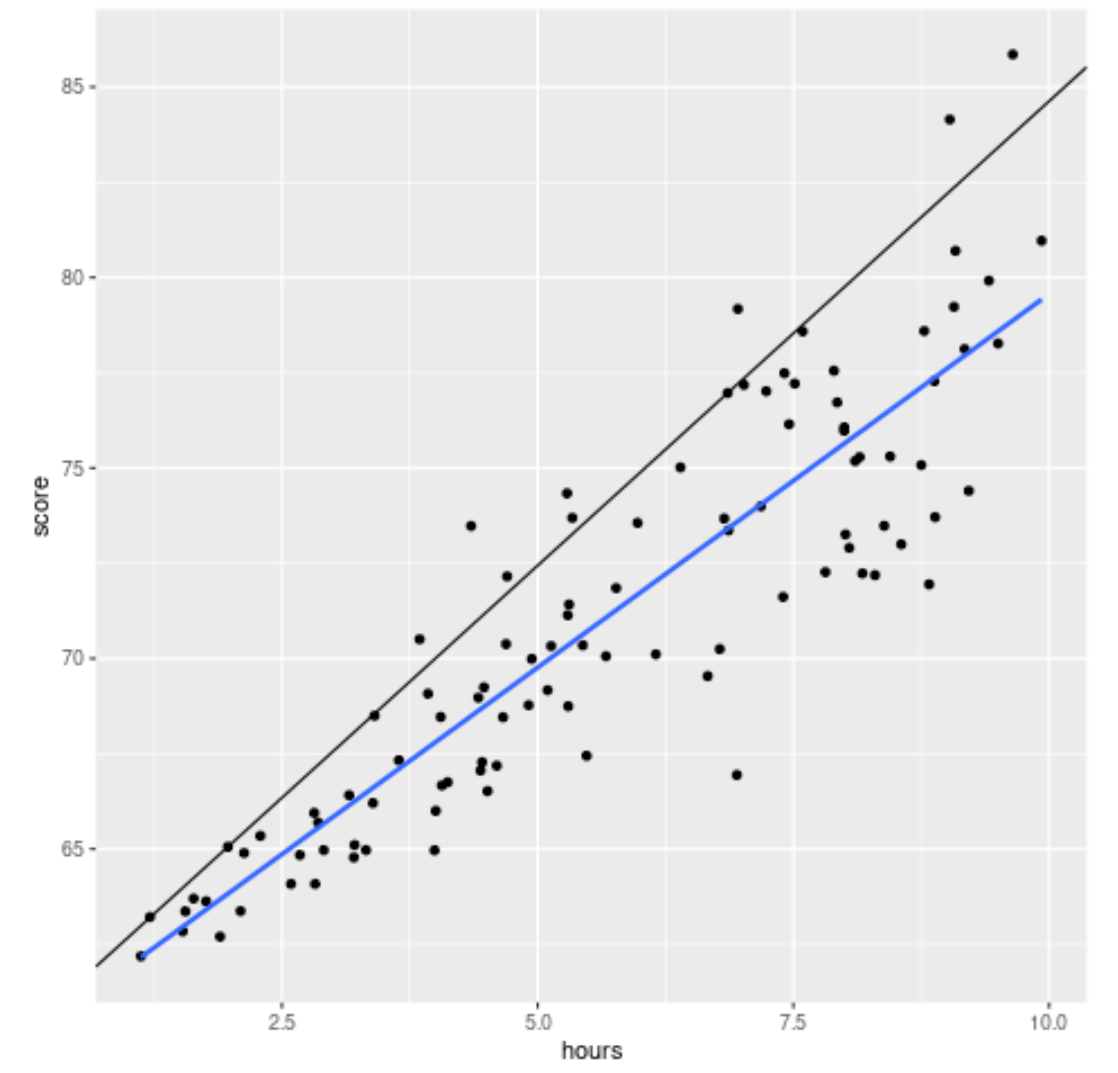
Чорна лінія відображає лінію квантильної регресії з поправкою на 90-й процентиль, а синя лінія відображає лінію простої лінійної регресії, яка оцінює середнє значення змінної відповіді.

Як і очікувалося, лінія простої лінійної регресії проходить через дані та показує нам розрахункове середнє значення балів за іспит за кожну годину.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати квадратичну регресію в R