Квартилі

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті ми пояснюємо, що таке квартилі. Ви знайдете визначення кожного квартиля, як їх обчислити та кілька конкретних прикладів. Ми також покажемо вам, як обчислити квартилі для згрупованих даних. Крім того, ви зможете розрахувати квартилі будь-якого набору даних за допомогою онлайн-калькулятора.

Що таке квартилі?

У статистиці квартилі – це три значення, які ділять набір упорядкованих даних на чотири рівні частини. Таким чином, перший, другий і третій квартилі становлять відповідно 25%, 50% і 75% усіх статистичних даних.

Квартилі представлені великою літерою Q та індексом квартиля, тому перший квартиль – Q ₁ , другий квартиль – Q ₂ , а третій квартиль – Q ₃ .

👉 Ви можете використовувати калькулятор нижче, щоб обчислити квартилі будь-якого набору даних.

Слід зазначити, що квартилі є мірою нецентрального положення так само, як квінтилі, децилі та процентилі. Ви можете перевірити, що таке кожен із цих типів квантилів на цій веб-сторінці.

перший квартиль

Перший квартиль , також званий квартилем 1, — це значення, що перевищує 25% статистичних даних у вибірці. Іншими словами, перший квартиль представляє понад 25% даних спостереження.

Перший квартиль виражається символом Q ₁ і використовується для позначення найменших значень даних у вибірці.

другий квартиль

Другий квартиль , також званий квартилем 2, — це значення, що перевищує 50% статистичних даних у вибірці. Таким чином, другий квартиль розділяє набір даних на дві половини та збігається з медіаною та п’ятим децилем.

Символом для другого квартиля є _Q2 .

третій квартиль

Третій квартиль , також званий 3-м квартилем, — це значення, яке перевищує 75% статистичних даних у вибірці. Іншими словами, третій квартиль представляє понад 75% зібраних даних.

Третій квартиль виражається символом Q ₃ і представляє найбільші значення у вибірці.

Як обчислити квартилі

Щоб обчислити положення квартилів набору статистичних даних, потрібно помножити кількість квартилів на суму загальної кількості даних плюс один і розділити результат на чотири.

Тому формула для квартилів виглядає наступним чином:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Будь ласка, зверніть увагу: ця формула повідомляє нам позицію квартиля, а не значення квартиля. Квартиль буде даними, розташованими в позиції, отриманій формулою.

Однак іноді результат цієї формули дає нам десяткове число. Тому ми повинні розрізняти два випадки залежно від того, чи є результат десятковим числом чи ні:

Якщо результатом формули є число без десяткової частини , квартиль — це дані, які знаходяться в позиції, наданій формулою вище.
Якщо результатом формули є число з десятковою частиною , значення квартиля обчислюється за такою формулою:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

Де x _i і x _i+1 — номери позицій, між якими знаходиться число, отримане за першою формулою, а d — десяткова частина числа, отриманого за першою формулою.

Тепер, можливо, обчислення квартилів для вас дуже складне, тому що потрібно враховувати багато речей. Але за допомогою двох прикладів у наступному розділі ви побачите, наскільки це насправді досить просто.

Примітка : у науковому співтоваристві немає єдиної думки щодо того, як обчислювати квартилі, тому ви можете знайти статистичну книгу, яка пояснює це дещо інакше.

Приклади обчислення квартилів

Щоб повністю зрозуміти, як обчислюються квартилі, ви знайдете дві розв’язані вправи нижче. У першому квартилі є цілими числами, а в другому квартилі є десятковими числами, тому ви можете бачити, які два випадки ви можете знайти.

Приклад 1

Обчисліть три квартилі наступного набору даних:

Як ми бачили вище, формула для визначення квартилів така:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

У цьому випадку n загальна кількість спостережень дорівнює 15, тому ми повинні замінити n на 15 і k на 1, щоб знайти перший квартиль:

$\cfrac{1\cdot (15+1)}{4}=4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_1=39$

Отже, перший квартиль – це число на четвертій позиції впорядкованого списку значень, яке в даному випадку дорівнює 39.

Таким же чином ми обчислюємо другий квартиль, замінюючи коефіцієнт k на 2:

$\cfrac{2\cdot (15+1)}{4}=8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_2=48$

Отже, квартиль 2 є восьмим числом у відсортованому списку, що відповідає значенню 48.

Нарешті, ми востаннє застосовуємо формулу з k =3, щоб обчислити третій квартиль:

$\cfrac{3\cdot (15+1)}{4}=12 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad Q_3=60$

Квартиль 3 відповідає даним на дванадцятій позиції, тобто 60.

Приклад 2

Знайдіть три квартилі таких рядів даних:

У цьому другому прикладі ми маємо 24 спостереження, тому числа, отримані з формули квартиля, будуть десятковими.

Спочатку ми обчислюємо позицію першого квартиля, замінюючи k замість 1 у загальній формулі:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (24+1)}{4}=6,25$

Але ми отримали десяткове число 6,25, тому перший квартиль лежить між шостим і сьомим даними, які дорівнюють 22 і 25 відповідно. Отже, щоб обчислити точний квартиль, нам потрібно застосувати таку формулу:

$Q=x_i+d\cdot (x_{i+1}-x_i)$

У цьому випадку x _i дорівнює 22, x _i+1 25, а d є десятковою частиною отриманого числа, тобто 0,25. ще:

$Q_1=22+0,25\cdot (25-22)=22,75$

Тепер ми виконуємо ту саму процедуру, щоб знайти другий квартиль:

$\cfrac{2\cdot (24+1)}{4}=12,5$

Знову ми отримуємо десяткове число з формули, у цьому випадку це 12,5. Тому ми повинні використовувати ту саму формулу з дванадцятим і тринадцятим числами в таблиці даних, які відповідають 49 і 50:

$Q_2=49+0,5\cdot (50-49)=49,5$

Нарешті, ми повторюємо той самий процес, щоб отримати третій квартиль:

$\cfrac{3\cdot (24+1)}{4}=18,75$

Але число 18,75 знаходиться між числом 18 і 19, тому третій квартиль буде знаходитися між значеннями цих позицій (71 і 73). Точніше, це буде значення, яке ми отримаємо з наступного виразу:

$Q_3=71+0,75\cdot (73-71)=72,5$

квартильний калькулятор

Підключіть набір статистичних даних до калькулятора нижче, щоб обчислити квартилі. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Квартилі в згрупованих даних

Щоб обчислити квартилі, коли дані згруповано в інтервали, нам спочатку потрібно знайти інтервал або бін, до якого потрапляє квартиль, використовуючи таку формулу:

$\cfrac{k\cdot (n+1)}{4} \qquad k=1, 2, 3$

Таким чином, квартиль буде в інтервалі, абсолютна кумулятивна частота якого безпосередньо більша за число, отримане за допомогою попереднього виразу.

І коли ми знаємо інтервал, до якого належить квартиль, ми повинні застосувати таку формулу, щоб знайти точне значення квартиля:

$Q_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3$

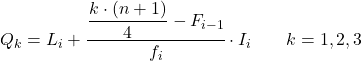
золото:

L _i — нижня межа інтервалу, в якому лежить квартиль.
n – загальна кількість спостережень.
F _i-1 – кумулятивна абсолютна частота попереднього інтервалу.
f _i — абсолютна частота інтервалу, в якому лежить квартиль.
I _i — ширина квартильного інтервалу.

Як приклад, ось вправа для обчислення квартилів у серії згрупованих даних:

Щоб обчислити перший квартиль, потрібно спочатку визначити інтервал, в який він потрапляє. Для цього застосовуємо таку формулу:

$\cfrac{k\cdot (n+1)}{4}$

$\cfrac{1\cdot (30+1)}{4} =7,75 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [50,60)$

Таким чином, перший квартиль буде в інтервалі, чия кумулятивна абсолютна частота одразу перевищує 7,75, у цьому випадку це інтервал [50,60), чия кумулятивна абсолютна частота дорівнює 15. І коли ми знаємо квартильний інтервал, ми використовуємо другу формулу процесу :

$Q_k=L_i+\cfrac{\displaystyle\frac{k\cdot (n+1)}{4}-F_{i-1}}{f_i}\cdot I_i$

$Q_1=50+\cfrac{\displaystyle\frac{1\cdot (30+1)}{4}-7}{8}\cdot 10=50,94$

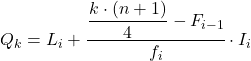
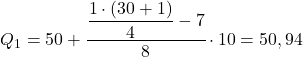
Ми знову застосовуємо ту саму процедуру, щоб отримати другий квартиль. Спочатку ми визначаємо інтервал, де лежить квартиль:

$\cfrac{2\cdot (30+1)}{4} =15,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Інтервал, кумулятивна абсолютна частота якого безпосередньо перевищує 15,5, становить [60,70), з кумулятивною абсолютною частотою 26. Таким чином, другий квартиль дорівнює:

$Q_2=60+\cfrac{\displaystyle\frac{2\cdot (30+1)}{4}-15}{11}\cdot 10=60,45$

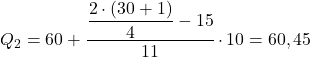
І, нарешті, ми повторюємо процес, щоб знайти третій квартиль. Спочатку ми обчислюємо інтервал, який містить квартиль:

$\cfrac{3\cdot (30+1)}{4} =22,5 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [60,70)$

Кумулятивна абсолютна частота безпосередньо над 23,25 дорівнює 26, отже діапазон третього квартиля [60,70]. Тому ми застосовуємо формулу для обчислення квартиля з цим інтервалом:

$Q_3=60+\cfrac{\displaystyle\frac{3\cdot (30+1)}{4}-15}{11}\cdot 10=67,5$

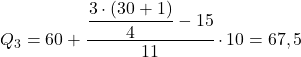
Для чого використовуються квартилі?

Квартилі є мірою позиції, тому вони використовуються, щоб знати, як позиціонуються дані. Іншими словами, значення трьох квартилів дозволяють нам дізнатися, чи є випадковий елемент даних у вибірці дуже великим, дуже малим або це середнє значення.

Якщо ми випадково беремо фрагмент даних із вибірки, ми можемо визначити, чи є його значення високим чи низьким, порівнюючи його з квартилями. Якщо значення випадкових даних менше першого квартиля, це буде маленьке значення, але якщо його значення більше третього квартиля, це буде велике значення. Так само, якщо значення зазначених даних знаходиться між першим і третім квартилем, це проміжне значення.

З іншого боку, квартилі також використовуються для обчислення інших статистичних показників, таких як інтерквартильний діапазон (або міжквартильний діапазон), і для побудови діаграм, таких як прямокутний графік (або прямокутний графік).

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке квартилі?

перший квартиль

другий квартиль

третій квартиль

Як обчислити квартилі

Приклади обчислення квартилів

Приклад 1

Приклад 2

квартильний калькулятор

Квартилі в згрупованих даних

Для чого використовуються квартилі?

Про автора

Редакція

Додати коментар