Як обчислити квартилі для згрупованих даних

Квартилі – це значення, які ділять набір даних на чотири рівні частини.

Щоб обчислити квартилі для згрупованих даних, можна скористатися такою формулою:

Q _i = L + (C/F) * (iN/4 – M)

золото:

• L : нижня межа інтервалу, який містить i- ^й квартиль
• C : Ширина класу
• F : частота інтервалу, який містить i- ^й квартиль
• N : Загальна частота
• M : Кумулятивна частота, що веде до інтервалу, який містить i- ^й квартиль

У наступному прикладі показано, як використовувати цю формулу на практиці.

Приклад: обчислення квартилів для згрупованих даних

Припустимо, що ми маємо такий розподіл частот:

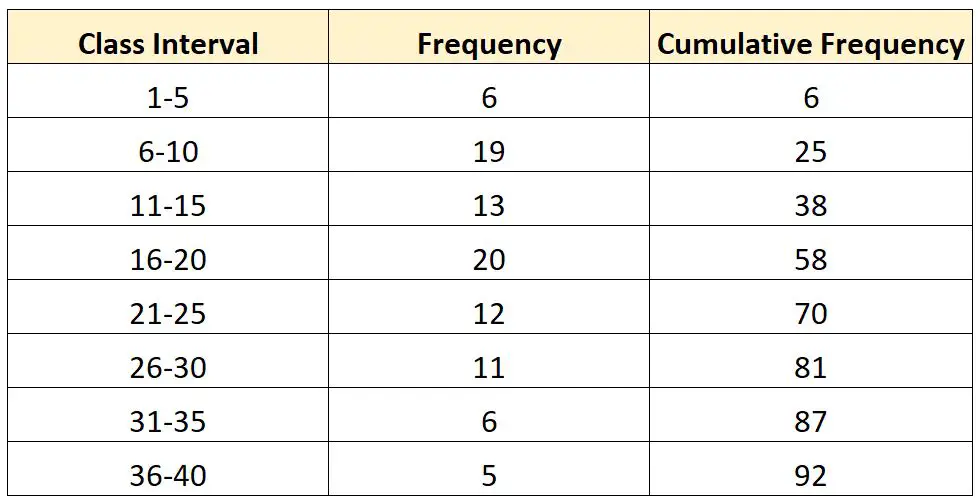
Тепер припустімо, що ми хочемо обчислити значення третього квартиля (Q ₃ ) цього розподілу.

Значення в третьому квартилі буде розташовано на позиції (iN/4) у розподілі.

Отже, (iN/4) = (3*92/4) = 69.

Інтервал, який містить третій квартиль, буде інтервалом 21-25 , оскільки 69 знаходиться між кумулятивними частотами 58 і 70.

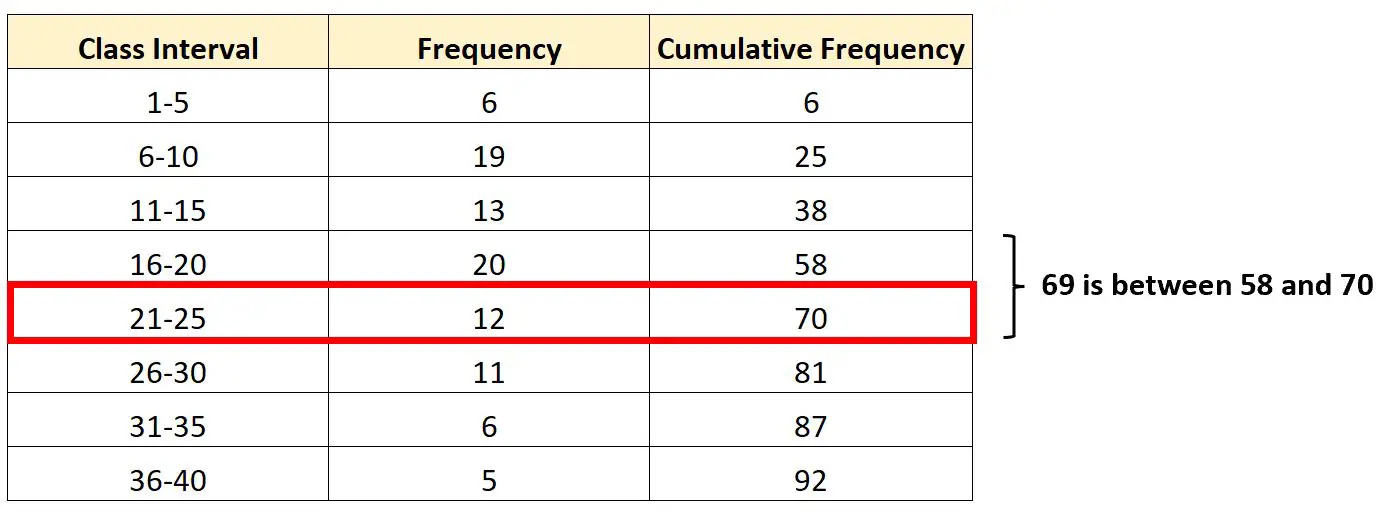
Знаючи це, ми можемо знайти кожне з необхідних значень для підключення до нашої формули:

L : нижня межа інтервалу, який містить i- ^й квартиль

• Нижня межа інтервалу 21 .

C : Ширина класу

• Ширина класу розраховується так: 25 – 21 = 4 .

F : частота інтервалу, який містить i- ^й квартиль

• Частота 21-25 класу – 12

N : Загальна частота

• Загальна кумулятивна частота в таблиці становить 92 .

M : Кумулятивна частота, що веде до інтервалу, який містить i- ^й квартиль

• Кумулятивна частота до класу 21-25 становить 58 .

Потім ми можемо підключити всі ці значення до попередньої формули, щоб знайти значення в третьому квартилі:

• Q _i = L + (C/F) * (iN/4 – M)
• Q ₃ = 21 + (4/12) * ((3)(92)/4 – 58)
• _Q3 = 24,67

Значення в третьому квартилі становить 24,67 .

Ви можете використовувати подібний підхід для обчислення значень першого та другого квартилів.

Додаткові ресурси

У наступних посібниках надається додаткова інформація про роботу зі згрупованими даними:

Як знайти середнє значення та стандартне відхилення згрупованих даних
Як знайти режим згрупованих даних
Як знайти медіану згрупованих даних
Згрупований або незгрупований розподіл частот