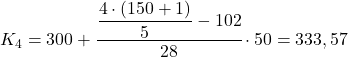Квінтилі (статистика)

за Редакція 5 Серпня, 2023 Статистика 0 коментарів

У цій статті ми пояснюємо, що таке квінтилі та як вони обчислюються. Ви знайдете кілька розв’язаних прикладів обчислення квінтилів і, крім того, ви зможете розрахувати квінтилі будь-якої статистичної вибірки за допомогою онлайн-калькулятора.

Що таке квінтилі?

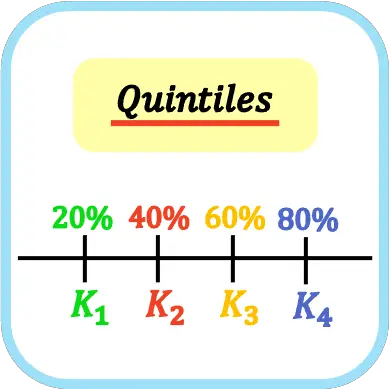
У статистиці квінтилі – це чотири значення, які ділять набір даних на п’ять рівних частин. Таким чином, перший, другий, третій і четвертий квінтилі становлять 20%, 40%, 60% і 80% даних вибірки відповідно.

Тобто значення третього квінтиля, наприклад, вище за 60% усіх зібраних даних, але нижче за решту даних.

Символом для квінтилів є велика літера K з індексом квінтиля, тобто перший квінтиль – K ₁ , другий квінтиль – K ₂ , третій квінтиль – K ₃ і четвертий квінтиль – K ₄ . Хоча це також може бути представлено буквою Q (не рекомендується, оскільки це створює плутанину з квартилями).

👉 Ви можете використовувати калькулятор нижче, щоб обчислити квінтилі для будь-якого набору даних.

Квінтилі є мірою нецентрального положення разом із квартилями, децилями та процентилями. Якщо вас цікавить більше, ви можете перевірити, що означає кожен із цих типів квантилів на нашому веб-сайті.

Слід зазначити, що квінтиль може мати інше визначення. В економіці квінтилі представляють відсоток населення, впорядковане за доходом, або, іншими словами, вони ранжують населення за рівнем доходу. Наприклад, перший квінтиль відповідає 20% найбідніших людей у популяції, другий квінтиль відповідає 40% населення з найнижчими доходами і так далі.

Як розрахувати квінтилі

Щоб обчислити положення квінтилів вибірки або статистичної сукупності, ви повинні помножити кількість квінтилів на суму загальної кількості даних плюс один і розділити результат на п’ять.

Отже, формула для квінтилів така:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Будь ласка, зверніть увагу: результат цієї формули повідомляє нам позицію квінтиля, а не його значення. Таким чином, квінтиль буде даними, розташованими в позиції, отриманій формулою.

Однак іноді результат цієї формули дає нам десяткове число, тому ми повинні розрізняти два випадки залежно від того, чи є результат десятковим числом чи ні:

Якщо результатом формули є число без десяткової частини , квінтиль — це дані, розташовані в позиції, передбаченій формулою вище.
Якщо результатом формули є число з десятковою частиною , значення квінтиля обчислюється за таким виразом:

$K=x_i+d\cdot (x_{i+1}-x_i)$

Де x _i і x _i+1 — номери позицій, між якими знаходиться число, отримане за першою формулою, а d — десяткова частина числа, отриманого за першою формулою.

Якщо ви злякалися, коли побачили стільки кроків для визначення квінтилів набору даних, не хвилюйтеся, це насправді досить просто. Прочитайте наступні два приклади, і ви напевно зрозумієте набагато краще.

Примітка : статистичне співтовариство все ще не зовсім погодилося щодо того, як обчислюються квінтилі, тому ви можете знайти книгу, яка пояснює це дещо інакше.

Приклади обчислення квінтилів

Нижче ми пропонуємо вам поетапно вирішити дві вправи щодо того, як отримати квінтилі з ряду даних. Отже, щоб ви могли побачити два можливі випадки, у першій вправі результати не є десятковими, а в другій вправі вони є.

Приклад 1

Обчисліть квінтилі таких рядів даних:

Як ви бачили в поясненні вище, формула для визначення положення квінтилів така:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Параметр n відноситься до загальної кількості даних, яка становить 49, тому, щоб знайти позицію першого квінтиля, нам потрібно замінити n на 49 і k на 1:

$\cfrac{1\cdot (49+1)}{5}=10 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_1=205$

З формули ми отримали число 10, яке означає, що квінтиль знаходиться на десятій позиції впорядкованого списку, що відповідає даним 205.

Щоб обчислити другий квінтиль, ви повинні використовувати ту саму формулу, але замінивши k на 2:

$\cfrac{2\cdot (49+1)}{5}=20 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_2=236$

Таким чином, другий квінтиль знаходиться на позиції номер 20 упорядкованого списку, тобто значення 236.

Знову ми повторюємо процес для визначення квінтиля 3, але, логічно, тепер ми замінюємо k на 3:

$\cfrac{3\cdot (49+1)}{5}=30 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_3=266$

Таким чином, третій квінтиль – це дані, розташовані в позиції 30, що відповідає 266.

Нарешті, ми знову застосовуємо формулу для розрахунку четвертого квінтиля:

$\cfrac{4\cdot (49+1)}{5}=40 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad K_4=286$

Таким чином, четвертий квінтиль знаходиться на позиції 40, тому четвертий квінтиль дорівнює 286.

Приклад 2

Обчисліть чотири квінтилі статистичних даних, зібраних у наступній таблиці:.

Так само, як і в попередньому прикладі, для отримання позицій квінтилів необхідно використовувати таку формулу:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

У цьому випадку розмір вибірки становить 42 спостереження, тому, щоб знайти позицію першого квінтиля, нам потрібно замінити параметр n на 42, а k на 1:

$\cfrac{1\cdot (42+1)}{5}=8,6$

Однак, на відміну від першого прикладу, цього разу формула дає нам десяткове число, тому нам потрібно застосувати таку формулу, щоб обчислити точний квінтиль:

$K=x_i+d\cdot (x_{i+1}-x_i)$

Число, отримане за першою формулою, дорівнює 8,6, тому перший квінтиль знаходиться між восьмим і дев’ятим даними, тобто 78 і 79 відповідно. Отже, x _i дорівнює 78, x _i+1 дорівнює 79 і d є десятковою частиною отриманого числа, тобто 0,6.

$K_1=78+0,6\cdot (79-78)=78,6$

Тепер ми повторюємо ту саму процедуру, щоб знайти другий квінтиль. Спочатку розрахуємо його положення:

$\cfrac{2\cdot (42+1)}{5}=17,2$

Але з формули ми отримуємо десяткове число між 17 і 18, так що другий квінтиль буде між сімнадцятою і вісімнадцятою позиціями, значення яких відповідають відповідно 109 і 112 впорядкованого списку. Тому ми застосовуємо другу формулу в процесі, щоб визначити точне значення квінтиля:

$K_2=109+0,2\cdot (112-109)=109,6$

Повторюємо метод для отримання третього квінтиля, спочатку визначаємо його положення:

$\cfrac{3\cdot (42+1)}{5}=25,8$

Розраховане число 25,8 означає, що значення квінтиля буде між двадцять п’ятою та двадцять шостою позицією, значення яких дорівнюють 134 і 141. Таким чином, розрахунок точного значення квінтиля:

$K_3=134+0,8\cdot (141-134)=139,6$

Нарешті, ми повторюємо ту саму процедуру востаннє, щоб обчислити квінтиль 4. Спочатку ми знаходимо його положення:

$\cfrac{4\cdot (42+1)}{5}=34,4$

Таким чином, точне значення четвертого квінтиля буде між 34 і 35, позиції якого відповідають даним 172 і 179. Таким чином, розрахунок четвертого квінтиля:

$K_4=172+0,4\cdot (179-172)=174,8$

Квінтильний калькулятор

Введіть набір статистичних даних у наступний калькулятор, щоб обчислити квінтилі. Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

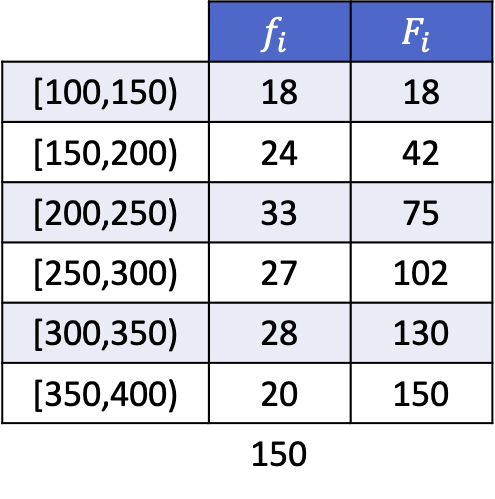
Квінтилі в згрупованих даних

Щоб обчислити квінтилі, коли дані згруповано в інтервали, ви повинні спочатку знайти його інтервал або клас за такою формулою:

$\cfrac{k\cdot (n+1)}{5} \qquad k=1, 2, 3,4$

Таким чином, квінтиль буде в інтервалі, абсолютна частота якого відразу перевищує число, отримане за допомогою попереднього виразу.

І коли ми знаємо інтервал, до якого належить квінтиль, ми повинні застосувати таку формулу, щоб знайти точне значення квінтиля:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i \qquad k=1,2,3,4$

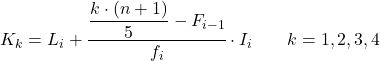
золото:

L _i – нижня межа інтервалу, в якому знаходиться квінтиль.
n – загальна кількість спостережень.
F _i-1 – кумулятивна абсолютна частота попереднього інтервалу.
f _i – абсолютна частота інтервалу, в якому знаходиться квінтиль.
I _i – ширина квінтильного інтервалу.

Отже, ви можете побачити, як це робиться, ось розв’язаний приклад обчислення квінтилів наступних рядів даних, згрупованих в інтервали:

Оскільки дані згруповані, ми повинні використовувати наступний метод для обчислення квінтилів: спочатку визначте діапазон, до якого потрапляє квінтиль, а потім знайдіть точне значення квінтиля.

Таким чином, щоб знайти інтервал, в якому знаходиться перший квінтиль, скористаємося такою формулою:

$\cfrac{k\cdot (n+1)}{5}$

$\cfrac{1\cdot (150+1)}{5} =30,2 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [150,200)$

Перший квінтиль буде в інтервалі, чия кумулятивна абсолютна частота одразу перевищує 30,2, у цьому випадку це інтервал [150 200), чия кумулятивна абсолютна частота дорівнює 42. І коли ми знаємо квінтильний інтервал, ми застосовуємо другу формулу процес визначення його точного значення:

$K_k=L_i+ \cfrac{\displaystyle\frac{k\cdot (n+1)}{5}-F_{i-1}}{f_i}\cdot I_i$

$K_1=150+\cfrac{\displaystyle\frac{1\cdot (150+1)}{5}-18}{24}\cdot 50=175,42$

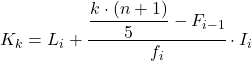
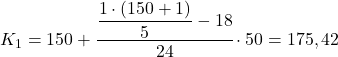
Тепер ми повторюємо ту саму процедуру для отримання другого квінтиля, спочатку обчисливши інтервал, в якому він лежить:

$\cfrac{2\cdot (150+1)}{5} =60,4 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [200,250)$

Кумулятивна абсолютна частота безпосередньо вище 60,4 становить 75, тому другий квінтильний діапазон становить [200 250). Тому ми підставляємо відповідні значення в другу формулу для розрахунку точного значення квінтиля:

$K_2=200+\cfrac{\displaystyle\frac{2\cdot (150+1)}{5}-42}{33}\cdot 50=227,88$

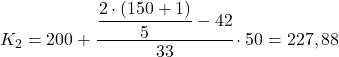
Ми виконуємо ту саму процедуру втретє, щоб отримати квінтиль 3. Спочатку ми визначаємо інтервал, де розташований квінтиль:

$\cfrac{3\cdot (150+1)}{5} =90,6 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [250,300)$

Квінтиль знаходиться в інтервалі [250,300), оскільки його кумулятивна абсолютна частота (102) знаходиться безпосередньо над 90,6. Тому розрахунок точного значення третього квінтиля виглядає наступним чином:

$K_3=250+\cfrac{\displaystyle\frac{3\cdot (150+1)}{5}-75}{27}\cdot 50=278,89$

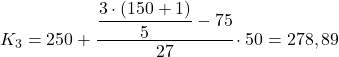
Нарешті ми знайдемо четвертий квінтиль. Як завжди, спочатку знаходимо його інтервал:

$\cfrac{4\cdot (150+1)}{5} =120,8 \quad \color{orange}\bm{\longrightarrow}\color{black}\quad [300,350)$

Інтервал, абсолютна частота якого безпосередньо перевищує 120,8, становить [300,350), значення якого дорівнює 130. Таким чином, точне значення четвертого квінтиля буде:

$K_4=300+\cfrac{\displaystyle\frac{4\cdot (150+1)}{5}-102}{28}\cdot 50=333,57$

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке квінтилі?

Як розрахувати квінтилі

Приклади обчислення квінтилів

Приклад 1

Приклад 2

Квінтильний калькулятор

Квінтилі в згрупованих даних

Про автора

Редакція

Додати коментар