Як виконати пробу шеффе в r

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Якщо загальне p-значення таблиці ANOVA нижче певного рівня значущості, тоді ми маємо достатньо доказів, щоб стверджувати, що принаймні одне з групових середніх відрізняється від інших.

Однак це не говорить нам , які групи відрізняються одна від одної. Це просто говорить нам про те, що не всі середні групові показники однакові.

Для того, щоб точно знати, які групи відрізняються одна від одної, нам потрібно виконати пост-хок тест , який може контролювати рівень помилок для сімейства .

Одним із найбільш часто використовуваних пост-тестів є тест Шеффе.

Цей посібник пояснює, як виконати тест Шеффе в R.

Приклад: тест Шеффе в Р

Припустімо, що вчитель хоче знати, чи призводять три різні методи навчання до різних результатів тестів серед учнів. Щоб перевірити це, вона випадковим чином призначає 10 студентів для використання кожної методики навчання та записує їхні результати іспитів.

Ми можемо використати наступні кроки в R, щоб підібрати односторонній дисперсійний аналіз, щоб перевірити різницю в середніх іспитових балах між трьома групами, і використати тест Шеффе, щоб точно визначити, які групи відрізняються.

Крок 1: Створіть набір даних.

Наступний код показує, як створити набір даних, що містить результати іспитів усіх 30 студентів:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Крок 2: Перегляньте результати іспиту для кожної групи.

У наведеному нижче коді показано, як створити коробкові діаграми для візуалізації розподілу результатів іспитів для кожної групи:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

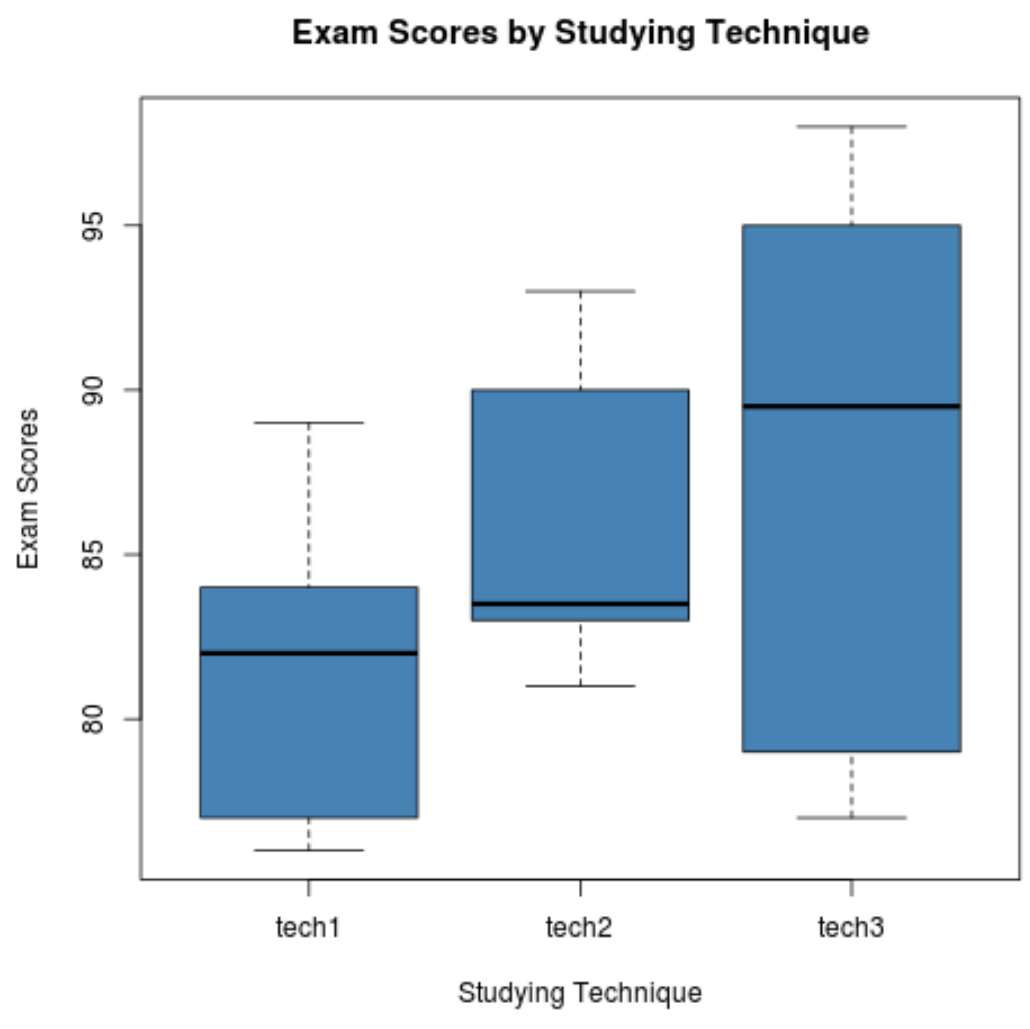
Крок 3: Виконайте односторонній дисперсійний аналіз.

У наведеному нижче коді показано, як виконати односторонній дисперсійний аналіз, щоб перевірити різницю між середніми оцінками іспиту в кожній групі:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Оскільки загальне значення p ( 0,0476 ) менше 0,05, це означає, що кожна група не має однакового середнього балу за іспит.

Далі ми виконаємо тест Шеффе, щоб визначити, які групи відрізняються.

Крок 4: Виконайте тест Шеффе.

Для виконання тесту Scheffe ми будемо використовувати функцію ScheffeTest() з пакету DescTools .

Наступний код показує, як використовувати цю функцію для нашого прикладу:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Спосіб інтерпретації результату такий:

• Середня різниця в результатах іспиту між технікою 2 і технікою 1 становить 4,2 . Відповідне р-значення для середньої різниці становить 0,2582 .
• Середня різниця в результатах обстеження між технікою 3 і технікою 1 становить 6,4 . Відповідне р-значення для середньої різниці становить 0,0519 .
• Середня різниця в результатах іспиту між технікою 3 і технікою 2 становить 2,2 . Відповідне р-значення для середньої різниці становить 0,6803 .

Залежно від того, який рівень значущості ми вирішимо використати, єдині дві групи, які статистично суттєво відрізняються, це Техніка 3 і Техніка 1.

Додаткові ресурси

Як виконати односторонній дисперсійний аналіз у R
Як виконати тест Тьюкі в R
Як виконати корекцію Бонферроні в R