Коефіцієнт детермінації (r у квадраті)

за Редакція 2 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке коефіцієнт детермінації (або R-квадрат) у статистиці. Отже, ви дізнаєтеся, як розрахувати коефіцієнт детермінації, як він інтерпретується і, крім того, онлайн-калькулятор для розрахунку коефіцієнта детермінації вибірки даних.

Що таке коефіцієнт детермінації (R у квадраті)?

Коефіцієнт детермінації , символом якого є R ² ( R у квадраті ), є статистичним показником, який вимірює відповідність регресійної моделі. Коефіцієнт детермінації показує, наскільки регресійна модель відповідає набору даних, тобто вказує на відсоток, пояснений регресійною моделлю.

Отже, чим вищий коефіцієнт детермінації, тим краща регресійна модель. Хоча ця умова не завжди виконується, ми в принципі зацікавлені в якомога більшому коефіцієнті детермінації. Нижче ми побачимо, як інтерпретувати коефіцієнт детермінації.

Формула визначального коефіцієнта

Коефіцієнт детермінації дорівнює одиниці мінус відношення між залишковою дисперсією та дисперсією залежної змінної. Коефіцієнт детермінації також можна розрахувати шляхом віднімання одиниці мінус сума квадратів із залишків із загальної суми квадратів.

Таким чином, формула для розрахунку коефіцієнта детермінації має такий вигляд:

формула для коефіцієнта детермінації, формула для r кв

золото:

$R^2$

– коефіцієнт детермінації.
$\sigma_r^2$

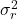
це залишкова дисперсія.
$\sigma^2$

є дисперсією залежної змінної Y.
$y_{i}$

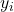
є значенням залежної змінної i.
$\widehat{y}_{i}$

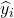
є значенням, апроксимованим регресійною моделлю для спостереження i.
$\overline{y}$

є середнім значенням залежної змінної для всіх спостережень.

👉 Ви можете скористатися калькулятором нижче, щоб обчислити коефіцієнт детермінації для будь-якого набору даних.

Для моделі лінійної регресії коефіцієнт детермінації еквівалентний квадрату коефіцієнта кореляції :

$R^2=\cfrac{\sigma_{XY}^2}{\sigma_X^2\sigma_Y^2}=\rho^2$

золото

$\sigma_{XY}^2$

– коваріація змінних X і Y,

$\sigma_X^2$

$\sigma_Y^2$

є дисперсіями незалежної змінної X і залежної змінної Y відповідно.

Калькулятор коефіцієнта детермінації

Підключіть зразки даних до калькулятора нижче, щоб підібрати просту модель лінійної регресії та обчислити її коефіцієнт детермінації. Потрібно розділити пари даних так, щоб у першому полі були лише значення незалежної змінної X, а в другому – лише значення залежної змінної Y.

Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Інтерпретація коефіцієнта детермінації

У цьому розділі ми побачимо, як інтерпретувати коефіцієнт детермінації, тому що немає сенсу знати значення коефіцієнта детермінації, якщо ви не знаєте, що він означає пізніше.

Значення коефіцієнта детермінації може коливатися від 0 до 1, однак, як правило, він виражається у відсотках, тому мінімум становить 0%, а максимум – 100%.

Що стосується інтерпретації коефіцієнта детермінації , то вище його значення означає, що регресійна модель краще пояснює вибірку даних. Таким чином, чим ближче коефіцієнт детермінації до 1, тим більше буде коригуватися модель. З іншого боку, чим ближче до 0, тим менш надійною буде створена регресійна модель.

Однак при порівнянні двох регресійних моделей модель з вищим коефіцієнтом регресії не завжди є кращою. Наприклад, регресійна модель може мати коефіцієнт регресії R ² = 100%, оскільки до моделі додано багато пояснювальних змінних і, отже, вона може ідеально пояснити всі спостереження. Але ця модель, безперечно, робить дуже поганий прогноз для нового значення, яке не використовувалося для побудови регресійної моделі.

Слід також мати на увазі, що отримана модель регресії відповідає попереднім припущенням. Таким чином, модель з дуже високим коефіцієнтом детермінації марна, якщо мінливість її залишків непостійна (гомоскедастичність).

Крім того, коефіцієнт детермінації представляє важливе обмеження, оскільки він не скасовує включення пояснювальних змінних. Логічно, чим більше пояснювальних змінних має регресійна модель, тим складнішою буде модель, але тим краще вона пояснюватиме спостережувані дані, а отже, тим вищим буде коефіцієнт детермінації. Проте скоригований коефіцієнт детермінації враховує кількість змінних у моделі (нижче ми побачимо, як він розраховується).

Підсумовуючи, коефіцієнт детермінації дуже корисний для аналізу регресійної моделі, оскільки він дає нам знати, наскільки добре регресійна модель відповідає набору даних. Однак для перегляду отриманої моделі слід також використовувати інші інструменти, наприклад статистичні графіки .

Скоригований коефіцієнт детермінації

Скоригований коефіцієнт детермінації , також званий скоригованим коефіцієнтом детермінації , вимірює відповідність регресійної моделі, беручи до уваги кількість пояснювальних змінних, включених до моделі.

Різниця між коефіцієнтом детермінації та скоригованим коефіцієнтом детермінації полягає в тому, що коефіцієнт детермінації вимірює якість коригування без урахування кількості змінних, з іншого боку, скоригований коефіцієнт детермінації вимірює якість коригування. штрафування за кожну додану змінну.

Формула для розрахунку скоригованого коефіцієнта детермінації виглядає наступним чином:

$\bar{R}^2=1-\cfrac{N-1}{N-k-1}\cdot (1-R^2)$

золото:

$\bar{R}^2$

– скоригований коефіцієнт детермінації.
$R^2$

– коефіцієнт детермінації.
$N$

це розмір вибірки.
$k$

кількість пояснювальних змінних у регресійній моделі.

Таким чином, скоригований коефіцієнт детермінації є кращим, ніж коефіцієнт детермінації для порівняння двох різних моделей, оскільки моделі можуть мати різну кількість пояснювальних змінних.

➤ Див.: Скоригований коефіцієнт детермінації

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше