Коефіцієнт фі: визначення та приклади

Коефіцієнт Phi (іноді його називають середньоквадратичним коефіцієнтом випадковості ) є мірою зв’язку між двома бінарними змінними.

Для таблиці 2×2, заданої для двох випадкових змінних x і y :

Коефіцієнт Phi можна розрахувати таким чином:

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

Приклад: розрахунок коефіцієнта Phi

Припустімо, ми хочемо знати, чи пов’язана стать із перевагами політичної партії. Ми беремо просту випадкову вибірку з 25 виборців і запитуємо їх про їхні переваги щодо політичної партії. У наступній таблиці представлені результати опитування:

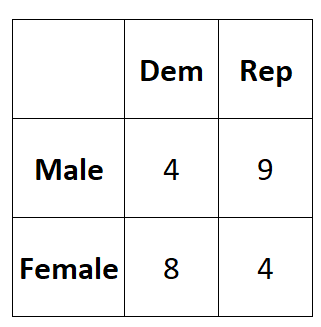
Ми можемо обчислити коефіцієнт Phi між двома змінними наступним чином:

Φ = (4*4-9*8) / √ (4+9)(8+4)(4+8)(9+4) = (16-72) / √ 24336 = -0,3589

Примітка. Ми також могли б обчислити це за допомогою калькулятора коефіцієнта Phi.

Як інтерпретувати коефіцієнт Phi

Подібно до коефіцієнта кореляції Пірсона, коефіцієнт Phi приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну залежність між двома змінними.
• 0 означає відсутність зв’язку між двома змінними.
• 1 вказує на абсолютно позитивний зв’язок між двома змінними.

Загалом, чим далі коефіцієнт Phi від нуля, тим сильніший зв’язок між двома змінними.

Іншими словами, чим далі коефіцієнт Phi від нуля, тим більше є доказів певного типу систематичної закономірності між двома змінними.

Додаткові ресурси

Керівництво по коефіцієнту кореляції Пірсона
Посібник із точного тесту Фішера
Посібник із тесту хі-квадрат незалежності