Корекція безперервності yate: визначення та приклад

Тест хі-квадрат незалежності використовується, щоб визначити, чи існує значний зв’язок між двома категоріальними змінними.

Цей тест використовує такі нульові та альтернативні гіпотези:

• H ₀ : (нульова гіпотеза) Дві змінні є незалежними.
• H ₁ : (альтернативна гіпотеза) Ці дві змінні не є незалежними. (тобто вони пов’язані)

Ми використовуємо таку формулу, щоб обчислити тестову статистику хі-квадрат x ² для цього тесту:

X ² = Σ(O _i -E _i ) ² / E _i

золото:

• Σ: химерний символ, що означає «сума»
• O: спостережуване значення
• E: очікуване значення

Цей тест припускає, що дискретні ймовірності частот у таблиці непередбачуваності можуть бути апроксимовані розподілом хі-квадрат, який є неперервним розподілом.

Однак це припущення, як правило, дещо невірне, а отримана в результаті тестова статистика має тенденцію бути зміщеною в бік підвищення.

Щоб виправити це зміщення, ми можемо застосувати корекцію безперервності Йейта , яка застосовує наступну корекцію до формули ^X2 :

X ² = Σ(|O _i -E _i | – 0,5) ² / E _i

Зазвичай ми використовуємо це виправлення лише тоді, коли принаймні одна клітинка в таблиці непередбачених випадків має очікувану частоту менше 5.

Приклад: застосування корекції безперервності Йейта

Припустімо, ми хочемо знати, чи пов’язана стать із перевагами політичної партії. Ми беремо просту випадкову вибірку з 40 виборців і запитуємо їх про їхні переваги щодо політичної партії. У наступній таблиці представлені результати опитування:

Ось як виконати тест хі-квадрат незалежності з корекцією безперервності Йейта:

Спостережувані значення:

Очікувані значення:

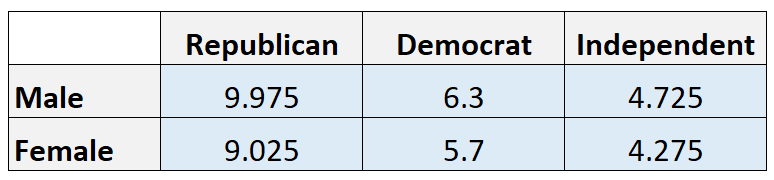
Примітка. Ми обчислюємо очікуване значення в кожній клітинці, помноживши загальну суму рядка на загальну суму стовпця, а потім поділивши на загальну суму. Наприклад, очікувана кількість чоловіків-республіканців становить (21*19)/40 = 9,975.

_{Статистика тесту} ^{хі –} _{квадрат} :

• (|8-9,975| – 0,5) ² / 9,975 = 0,218
• (|9-6,3| – 0,5) ² / 6,3 = 0,768
• (|4-4,725| – 0,5) ² / 4,725 = 0,011
• (|11-9,025| – 0,5) ² / 9,025 = 0,241
• (|3-5,7| – 0,5) ² / 5,7 = 0,849
• (|5-4,275| – 0,5) ² / 4,275 = 0,012

^Отже ,

P-value: відповідно до калькулятора хі-квадрат до P-value , p-value, яке відповідає статистиці тесту хі-квадрат із 2 ступенями свободи, становить 0,3501 .

Оскільки це p-значення не менше 0,05, ми не зможемо відхилити нульову гіпотезу. Це означає, що ми не маємо достатніх доказів, щоб стверджувати, що існує зв’язок між статтю та уподобаннями політичних партій.