Як створити кореляційну матрицю в r (4 приклади)

Кореляційна матриця – це квадратна таблиця, яка показує коефіцієнти кореляції між змінними в наборі даних.

Це забезпечує швидкий спосіб зрозуміти міцність лінійних зв’язків, які існують між змінними в наборі даних.

Є чотири поширені способи створення кореляційної матриці в R:

Спосіб 1: функція cor (для отримання простої матриці коефіцієнтів кореляції)

 cor(df)

Спосіб 2: функція rcorr (для отримання p-значень коефіцієнтів кореляції)

 library (Hmisc)

rcorr( as.matrix (df))

Метод 3: функція corrplot (для візуалізації кореляційної матриці)

 library (corplot)

corrplot(cor(df))

Спосіб 4: функція ggcorrplot (для візуалізації кореляційної матриці)

 library (ggcorrplot)

ggcorrplot(cor(df))

У наведених нижче прикладах показано, як використовувати кожен метод із таким кадром даних у R:

 #create data frame
df <- data. frame (assists=c(4, 5, 5, 6, 7, 8, 8, 10),
                 rebounds=c(12, 14, 13, 7, 8, 8, 9, 13),
                 points=c(22, 24, 26, 26, 29, 32, 20, 14))

#view data frame
df

  assists rebound points
1 4 12 22
2 5 14 24
3 5 13 26
4 6 7 26
5 7 8 29
6 8 8 32
7 8 9 20
8 10 13 14

Приклад 1: функція cor

Ми можемо використати функцію R base cor() , щоб створити кореляційну матрицю, яка показує коефіцієнти кореляції між кожною змінною в нашому кадрі даних:

 #create correlation matrix
cor(df)

            assists rebound points
assists 1.0000000 -0.2448608 -0.3295730
rebounds -0.2448608 1.0000000 -0.5220917
points -0.3295730 -0.5220917 1.0000000

Усі коефіцієнти кореляції по діагоналі таблиці дорівнюють 1, оскільки кожна змінна ідеально корелює сама із собою.

Усі інші коефіцієнти кореляції вказують на кореляцію між різними попарними комбінаціями змінних. Наприклад:

• Коефіцієнт кореляції між передачами та підбираннями становить -0,245 .
• Коефіцієнт кореляції між передачами та очками становить -0,330 .
• Коефіцієнт кореляції між підбираннями та очками становить -0,522 .

Приклад 2: функція rcorr

Ми можемо використати функцію rcorr() із пакета Hmisc у R, щоб створити кореляційну матрицю, яка показує коефіцієнти кореляції між кожною змінною в нашому кадрі даних:

 library (Hmisc)

#create matrix of correlation coefficients and p-values
rcorr( as.matrix (df))

         assists rebound points
assists 1.00 -0.24 -0.33
rebounds -0.24 1.00 -0.52
points -0.33 -0.52 1.00

n=8 

P
         assists rebound points
assists 0.5589 0.4253
rebounds 0.5589 0.1844
points 0.4253 0.1844

Перша матриця показує коефіцієнти кореляції між змінними, а друга матриця показує відповідні p-значення.

Наприклад, коефіцієнт кореляції між передачами та підбираннями становить -0,24 , а p-значення цього коефіцієнта кореляції становить 0,5589 .

Це говорить нам про те, що кореляція між двома змінними негативна, але це не є статистично значущою кореляцією, оскільки p-значення не менше 0,05.

Приклад 3: функція corrplot

Ми можемо використати функцію corrplot() із пакету corrplot у R, щоб візуалізувати кореляційну матрицю:

 library (corplot)

#visualize correlation matrix
corrplot(cor(df))

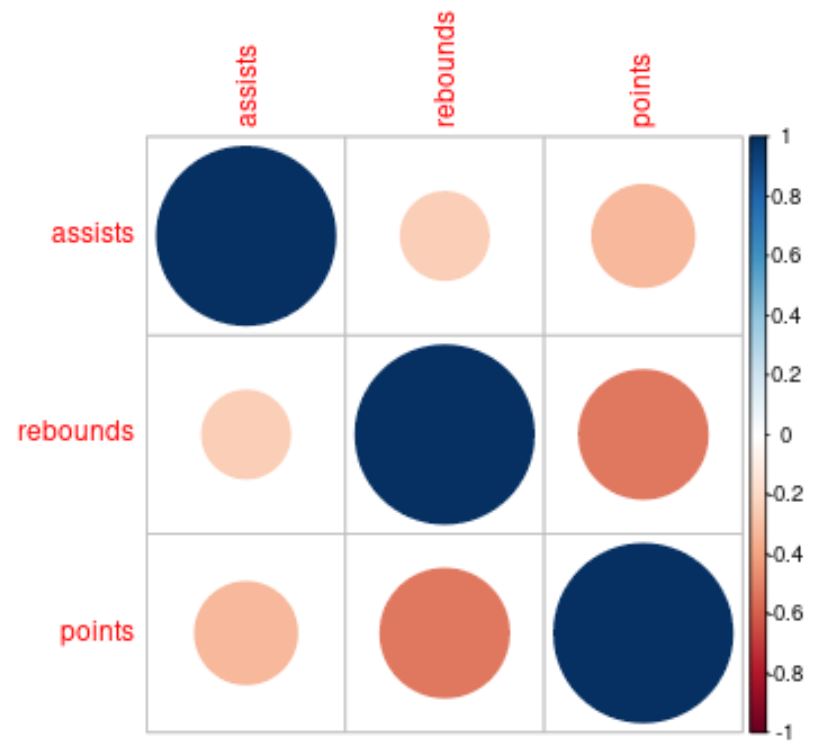
Колір і розмір кіл у кореляційній матриці допомагають нам візуалізувати кореляції між кожною змінною.

Наприклад, коло, де перетинаються змінні передачі та підбирання, маленьке та світло-червоне, що говорить нам про те, що кореляція слабка та негативна.

Приклад 4: функція corrplot

Ми можемо використати функцію ggcorrplot() із пакету ggcorrplot у R, щоб візуалізувати кореляційну матрицю:

 library (ggcorrplot)

#visualize correlation matrix
ggcorrplot(cor(df))

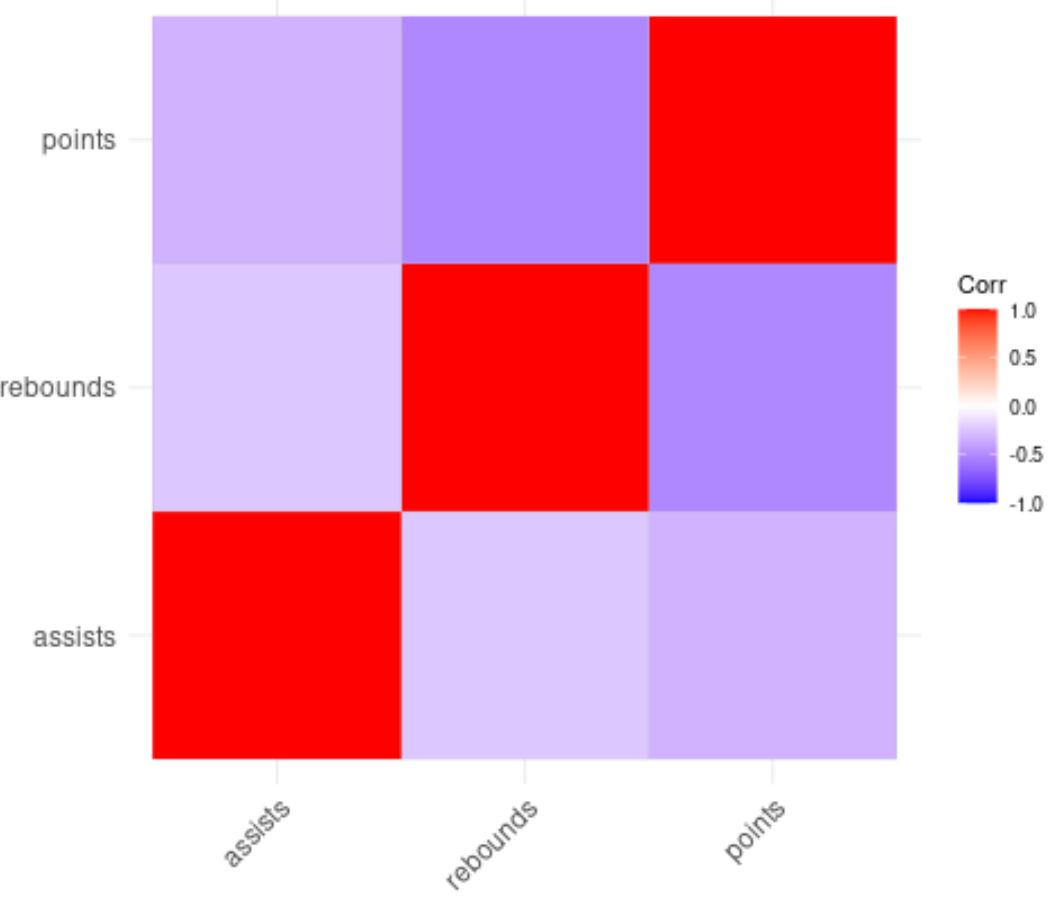
Колір квадратів у кореляційній матриці допомагає нам візуалізувати кореляції між кожною змінною.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як розрахувати кореляцію рангів Спірмена в R
Як обчислити часткову кореляцію в R
Як розрахувати ковзну кореляцію в R