Як виконати кореляційний тест у r (з прикладами)

Одним із способів кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який є мірою лінійного зв’язку між двома змінними .

Він завжди приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Щоб визначити, чи є коефіцієнт кореляції статистично значущим, ви можете обчислити відповідний t-показник і p-значення.

Формула для розрахунку t-показника коефіцієнта кореляції (r):

t = r * √ n-2 / √ 1-r ²

P-значення обчислюється як відповідне двостороннє p-значення для t-розподілу з n-2 ступенями свободи.

Приклад: тест кореляції в R

Щоб визначити, чи є коефіцієнт кореляції між двома змінними статистично значущим, ви можете виконати кореляційний тест у R за допомогою такого синтаксису:

cor.test(x, y, method=c(“pearson”, “kendall”, “spearman”))

золото:

• x, y: вектори цифрових даних.
• метод: метод, що використовується для обчислення кореляції між двома векторами. За замовчуванням — «Pearson».

Наприклад, припустимо, що ми маємо наступні два вектори в R:

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

Перш ніж виконувати кореляційний тест між двома змінними, ми можемо створити швидку діаграму розсіювання, щоб візуалізувати їхній зв’язок:

 #create scatterplot
plot(x, y, pch= 16 )

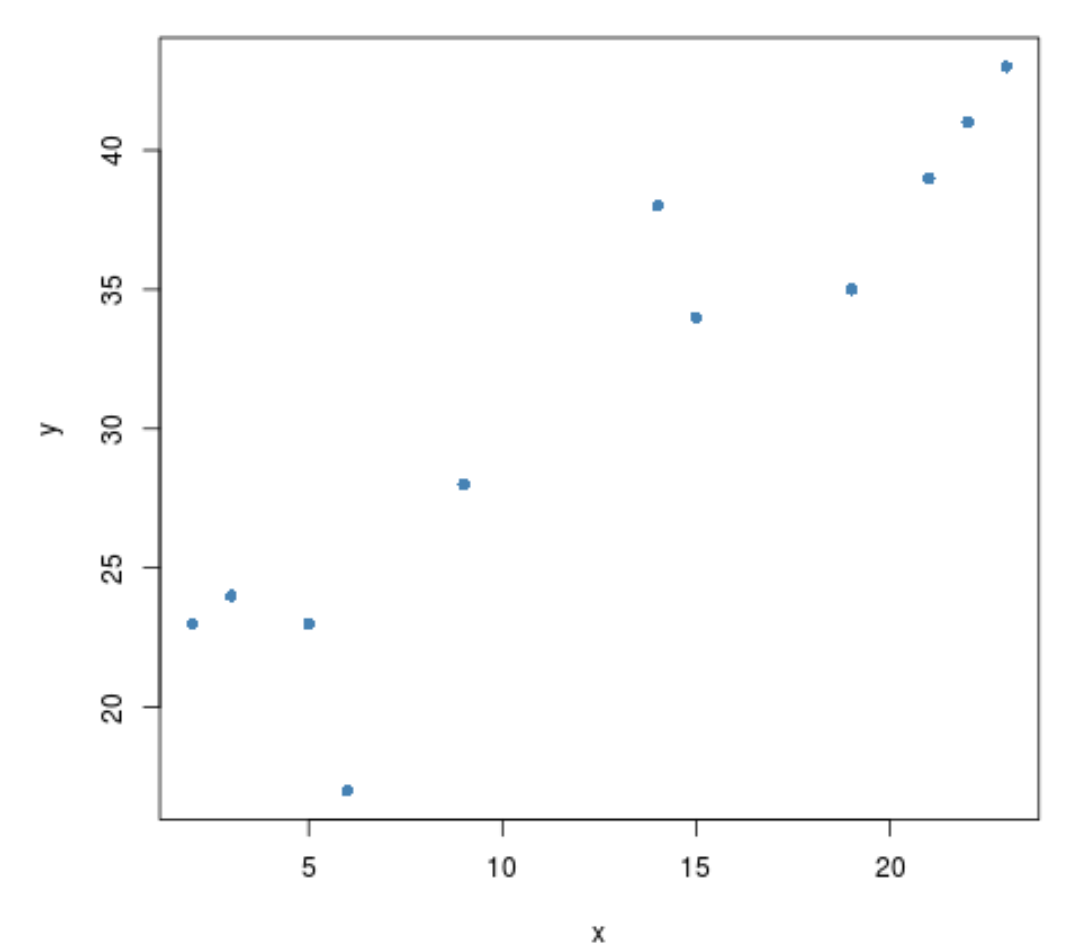
Здається, існує позитивна кореляція між двома змінними. Тобто, коли один збільшується, другий має тенденцію до зростання.

Щоб перевірити, чи ця кореляція є статистично значущою, ми можемо виконати кореляційний тест:

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

Коефіцієнт кореляції між двома векторами виявляється рівним 0,9279869 .

Статистика тесту дорівнює 7,8756 , а відповідне p-значення становить 1,35e-05 .

Оскільки це значення менше 0,05, ми маємо достатньо доказів, щоб стверджувати, що кореляція між двома змінними є статистично значущою.

Додаткові ресурси

Наступні посібники надають додаткову інформацію про коефіцієнти кореляції:

Вступ до коефіцієнта кореляції Пірсона
Що вважається «сильною» кореляцією?
П’ять гіпотез кореляції Пірсона