Як обчислити кореляцію в sas (з прикладами)

Одним із способів кількісного визначення зв’язку між двома змінними є використання коефіцієнта кореляції Пірсона , який вимірює лінійний зв’язок між двома змінними .

Він завжди приймає значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Чим далі коефіцієнт кореляції від нуля, тим сильніший зв’язок між двома змінними.

У наступних прикладах показано, як використовувати proc corr у SAS для обчислення коефіцієнта кореляції між змінними в інтегрованому наборі даних SAS під назвою Fish , який містить різні вимірювання для 159 різних риб, виловлених в озері у Фінляндії.

Ми можемо використовувати proc print для відображення перших 10 спостережень цього набору даних:

 /*view first 10 observations from Fish dataset*/
proc print data =sashelp.Fish( obs = 10 );

run ;

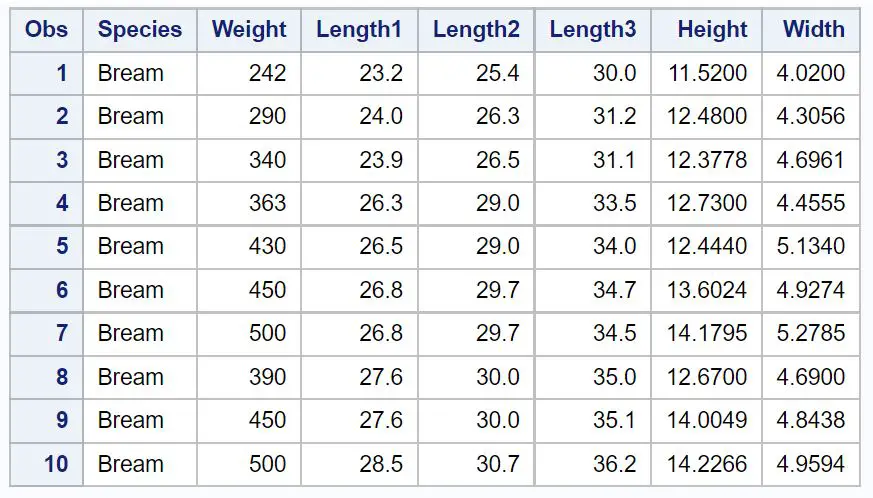
Приклад 1: Кореляція між двома змінними

Ми можемо використати такий код, щоб обчислити коефіцієнт кореляції Пірсона між змінними Height і Width:

 /*calculate correlation coefficient between Height and Width*/
proc corr data =sashelp.fish;
	var HeightWidth;

run ;

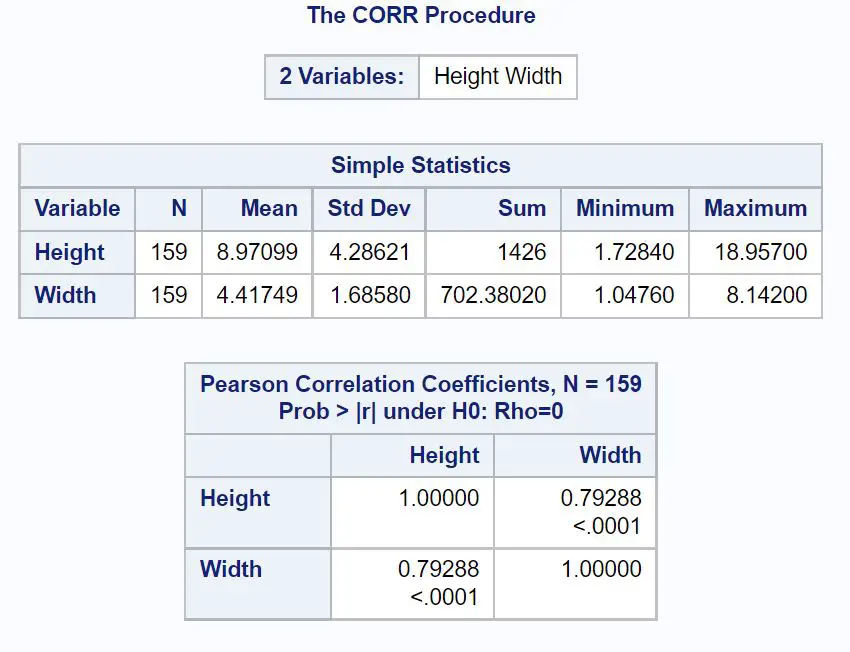
Перша таблиця відображає підсумкову статистику для висоти та ширини.

Друга таблиця відображає коефіцієнт кореляції Пірсона між двома змінними, включаючи значення p , яке повідомляє нам, чи є кореляція статистично значущою.

З результату ми бачимо:

• Коефіцієнт кореляції Пірсона: 0,79288
• Р-значення: <0,0001

Це говорить нам про те, що існує сильна позитивна кореляція між висотою та шириною, і що кореляція є статистично значущою, оскільки p-значення менше α = 0,05.

За темою: що вважається «сильною» кореляцією?

Приклад 2: Кореляція між усіма змінними

Ми можемо використати такий код, щоб обчислити коефіцієнт кореляції Пірсона між усіма попарними комбінаціями змінних у наборі даних:

 /*calculate correlation coefficient between all pairwise combinations of variables*/
proc corr data =sashelp.fish;

run;

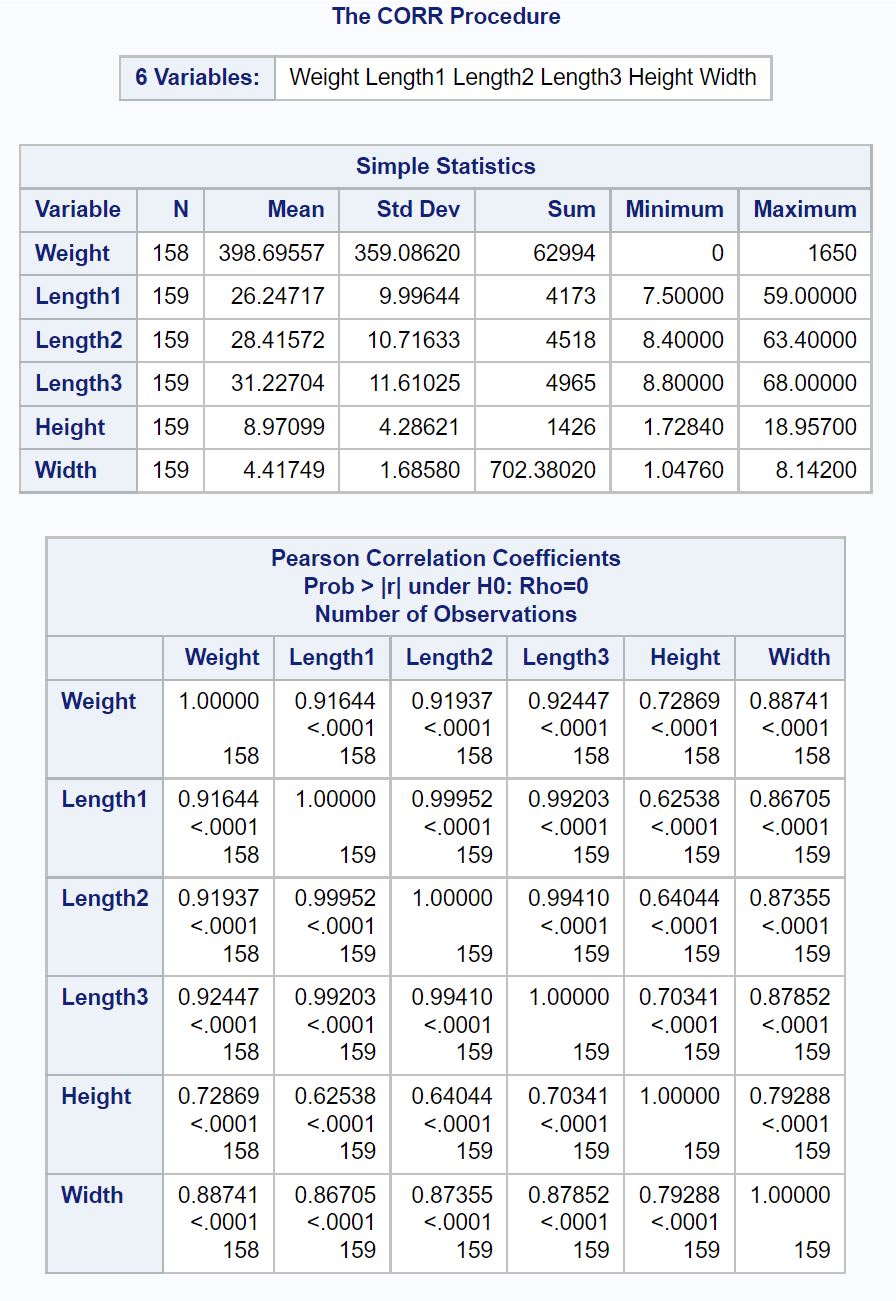
Результат відображає кореляційну матрицю , яка містить коефіцієнт кореляції Пірсона та відповідні p-значення для кожної попарної комбінації числових змінних у наборі даних.

Наприклад:

• Коефіцієнт кореляції Пірсона між вагою та довжиною1 становить 0,91644.
• Коефіцієнт кореляції Пірсона між вагою та довжиною2 становить 0,91937.
• Коефіцієнт кореляції Пірсона між вагою та довжиною3 становить 0,92447.

І так далі.

Приклад 3: Візуалізуйте кореляцію за допомогою діаграми розсіювання

Ми також можемо використовувати функцію plots для створення діаграми розсіювання для візуалізації кореляції між двома змінними:

 /*visualize correlation between Height and Width*/
proc corr data =sashelp.fish plots =scatter( nvar =all);;
	var HeightWidth;

run; 

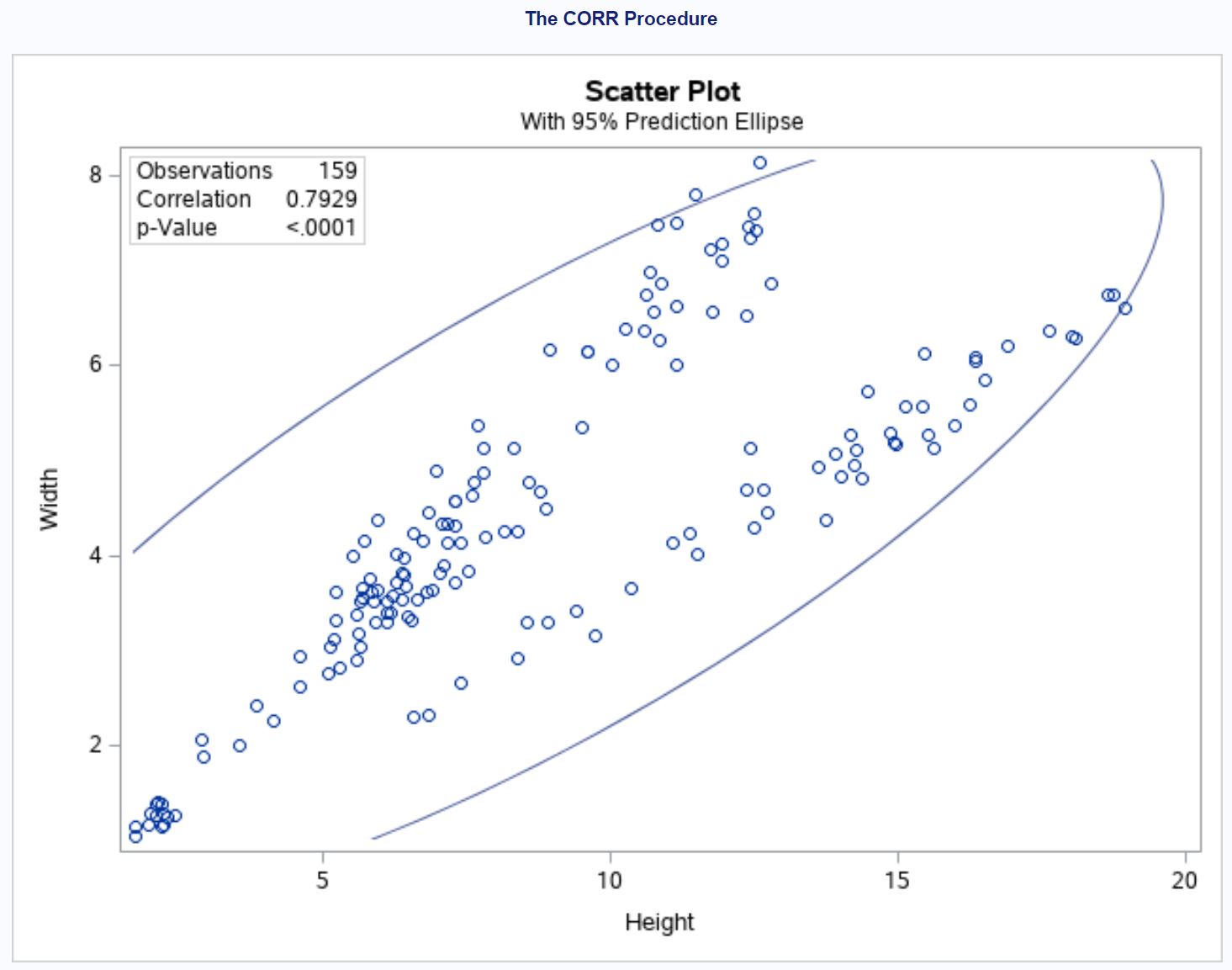
На графіку ми бачимо сильну позитивну кореляцію між висотою та шириною. Зі збільшенням висоти ширина також має тенденцію до збільшення.

У верхньому лівому куті графіка ми також можемо побачити загальну кількість використаних спостережень, коефіцієнт кореляції та p-значення коефіцієнта кореляції.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові операції в SAS:

Як створити частотні таблиці в SAS
Як розрахувати описову статистику в SAS