Кореляція vs. асоціація: яка різниця?

Два терміни, які іноді використовуються як синоніми, це кореляція та асоціація . Однак у сфері статистики ці два терміни мають дещо різні значення.

Зокрема, коли ми використовуємо слово кореляція , ми зазвичай говоримо про коефіцієнт кореляції Пірсона . Це міра лінійного зв’язку між двома випадковими змінними X і Y. Вона має значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

І навпаки, коли статистики використовують слово асоціація , вони можуть говорити про будь-який зв’язок між двома змінними, незалежно від того, лінійний чи нелінійний.

Щоб проілюструвати цю думку, розглянемо наступні приклади.

Візуалізація кореляції та асоціації з хмарами точок

Ми використовуємо два слова, щоб описати кореляцію між двома випадковими змінними:

1 напрямок

• Позитивний: дві випадкові змінні мають позитивну кореляцію, якщо Y має тенденцію до зростання зі збільшенням X.
• Негативний: дві випадкові змінні мають негативну кореляцію, якщо Y має тенденцію до зменшення зі збільшенням X.

2. Міцність

• Низька: дві випадкові змінні мають низьку кореляцію, якщо точки на діаграмі розсіювання рідко розсіяні.
• Сильна: Дві випадкові змінні мають сильну кореляцію, якщо точки на діаграмі розсіювання тісно згруповані разом.

Наступні діаграми розсіювання ілюструють приклади кожного типу кореляції:

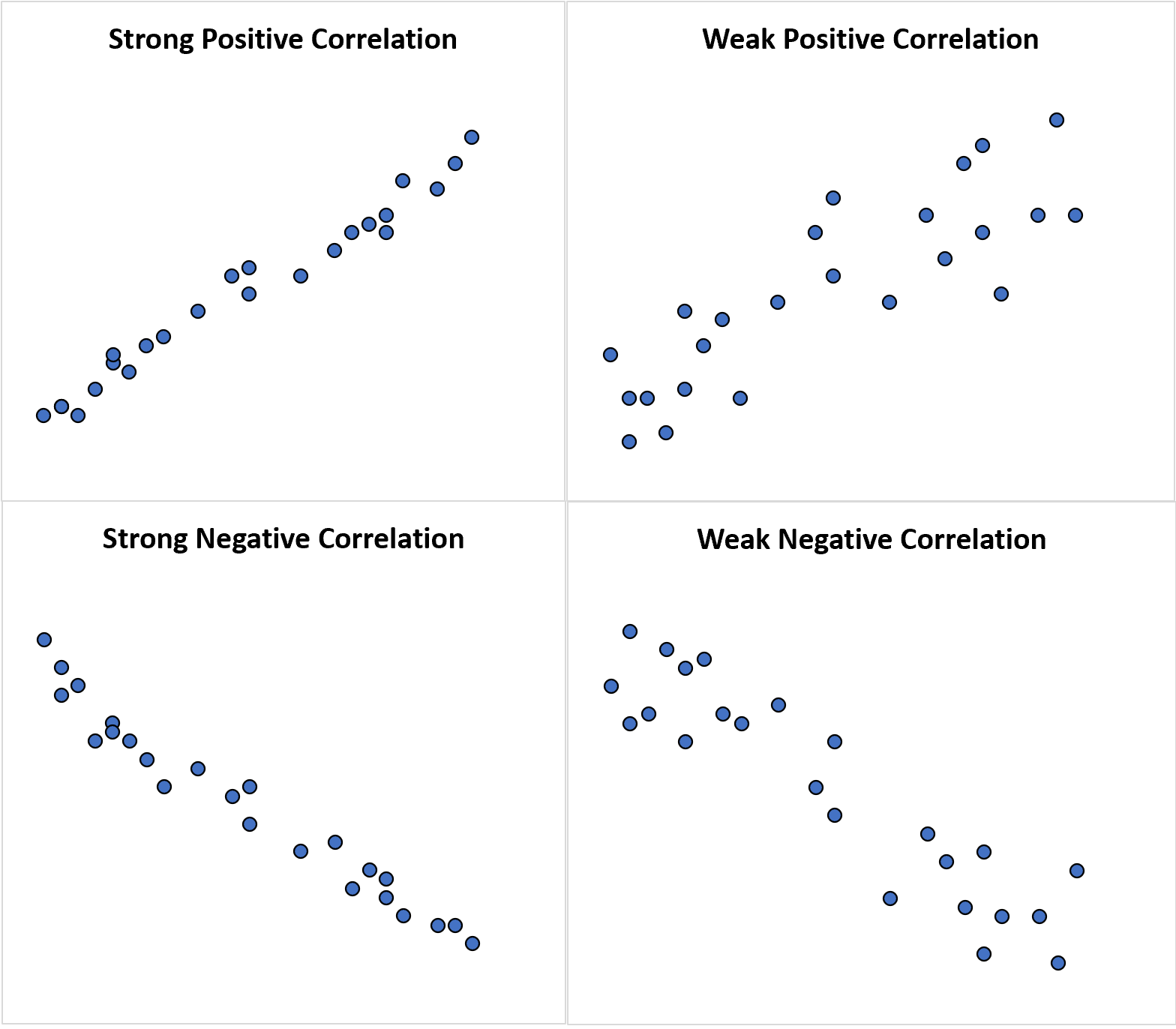
Порівняно з кореляцією слово асоціації може сказати нам, чи існує зв’язок між двома випадковими змінними: лінійним чи нелінійним.

Наступні діаграми розсіювання ілюструють деякі приклади:

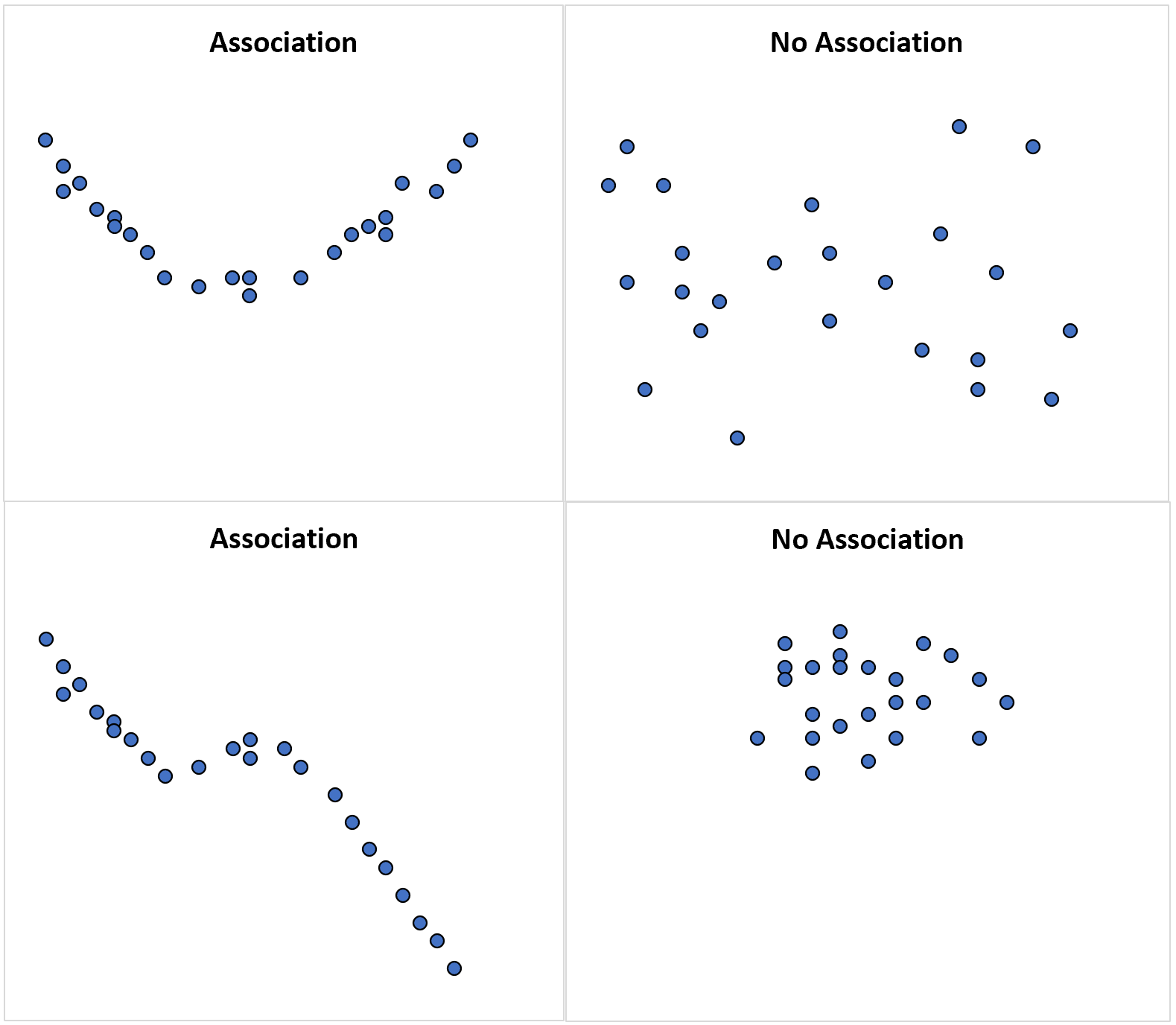
Діаграма розсіювання у верхньому лівому куті ілюструє квадратичний зв’язок між двома випадковими змінними, тобто зв’язок між двома змінними існує , але він не є лінійним.

Якби ми розрахували кореляцію між двома змінними, вона, ймовірно, була б близькою до нуля, оскільки між ними немає лінійного зв’язку.

Однак просте знання того, що кореляція між двома змінними дорівнює нулю, може ввести в оману, оскільки приховує той факт, що натомість існує нелінійний зв’язок.

Кореляція vs. асоціації: узагальн

Терміни кореляція та асоціація мають такі подібності та відмінності:

Подібності:

• Обидва терміни використовуються для опису того, чи існує залежність між двома випадковими величинами.
• Обидва терміни можуть використовувати діаграми розсіювання для аналізу зв’язку між двома випадковими величинами.

відмінності:

• Кореляція може лише сказати нам, чи дві випадкові змінні мають лінійний зв’язок, тоді як асоціація може сказати нам, чи дві випадкові змінні мають лінійний чи нелінійний зв’язок.
• Кореляція кількісно визначає зв’язок між двома випадковими змінними, використовуючи число від -1 до 1, але асоціація не використовує конкретне число для кількісної оцінки зв’язку.

Додаткові ресурси

Вступ до коефіцієнта кореляції Пірсона
Знайомство з хмарами точок
Кореляція проти регресії: у чому різниця?