Кореляція проти регресії: у чому різниця?

Кореляція та регресія — це два споріднені, але не зовсім однакові статистичні терміни.

У цьому підручнику ми надамо коротке пояснення обох термінів і пояснимо, чим вони схожі та чим відрізняються.

Що таке кореляція?

Кореляція вимірює лінійний зв’язок між двома змінними x і y . Він має значення від -1 до 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Наприклад, припустімо, що ми маємо такий набір даних, який містить дві змінні: (1) Вивчені години та (2) Оцінки за іспити, отримані для 20 різних студентів:

Якби ми створили діаграму розсіювання вивчених годин і результатів іспитів, це виглядало б ось як:

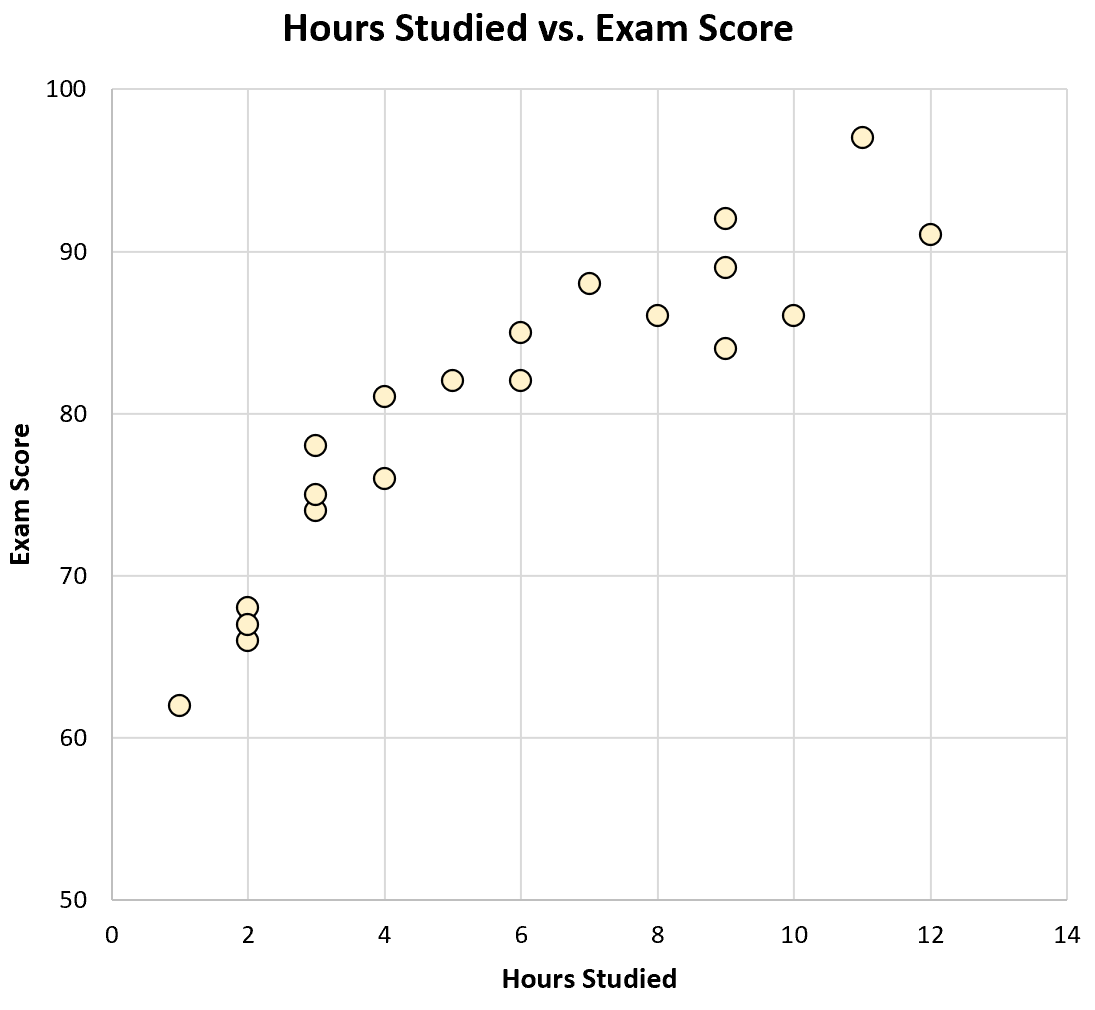
Просто подивившись на графік, ми можемо побачити, що студенти, які навчаються більше, як правило, мають кращі результати на іспитах. Іншими словами, ми можемо візуально побачити, що між двома змінними існує позитивна кореляція .

Використовуючи калькулятор, ми можемо побачити, що кореляція між цими двома змінними становить r = 0,915 . Це значення, близьке до 1, підтверджує наявність сильної позитивної кореляції між двома змінними.

Що таке регресія?

Регресія — це метод, який ми можемо використовувати, щоб зрозуміти, як зміна значень змінної x впливає на значення змінної y .

Регресійна модель використовує одну змінну, x , як змінну-прогноз, а іншу змінну, y , як змінну відповіді . Потім він знаходить рівняння наступної форми, яке найкраще описує зв’язок між двома змінними:

ŷ = b ₀ + b ₁ x

золото:

• ŷ: прогнозоване значення змінної відповіді
• b ₀ : ордината в початку координат (значення y, коли x дорівнює нулю)
• b ₁ : Коефіцієнт регресії (середнє збільшення y для збільшення x на одну одиницю)
• x: значення передбачуваної змінної

Наприклад, розглянемо наш попередній набір даних:

Використовуючи калькулятор лінійної регресії , ми виявили, що наступне рівняння найкраще описує зв’язок між цими двома змінними:

Прогнозована оцінка за іспит = 65,47 + 2,58*(вивчені години)

Спосіб інтерпретації цього рівняння:

• Прогнозований бал іспиту для студента, який вивчає нуль годин, становить 65,47 .
• Підвищення середнього балу за іспит, пов’язане з додатковою годиною навчання, становить 2,58 .

Ми також можемо використовувати це рівняння, щоб передбачити оцінку, яку отримає студент на основі кількості вивчених годин.

Наприклад, студент, який навчається 6 годин, повинен отримати оцінку 80,95 :

Прогнозована оцінка за іспит = 65,47 + 2,58*(6) = 80,95 .

Ми також можемо побудувати це рівняння у вигляді лінії на точковій діаграмі:

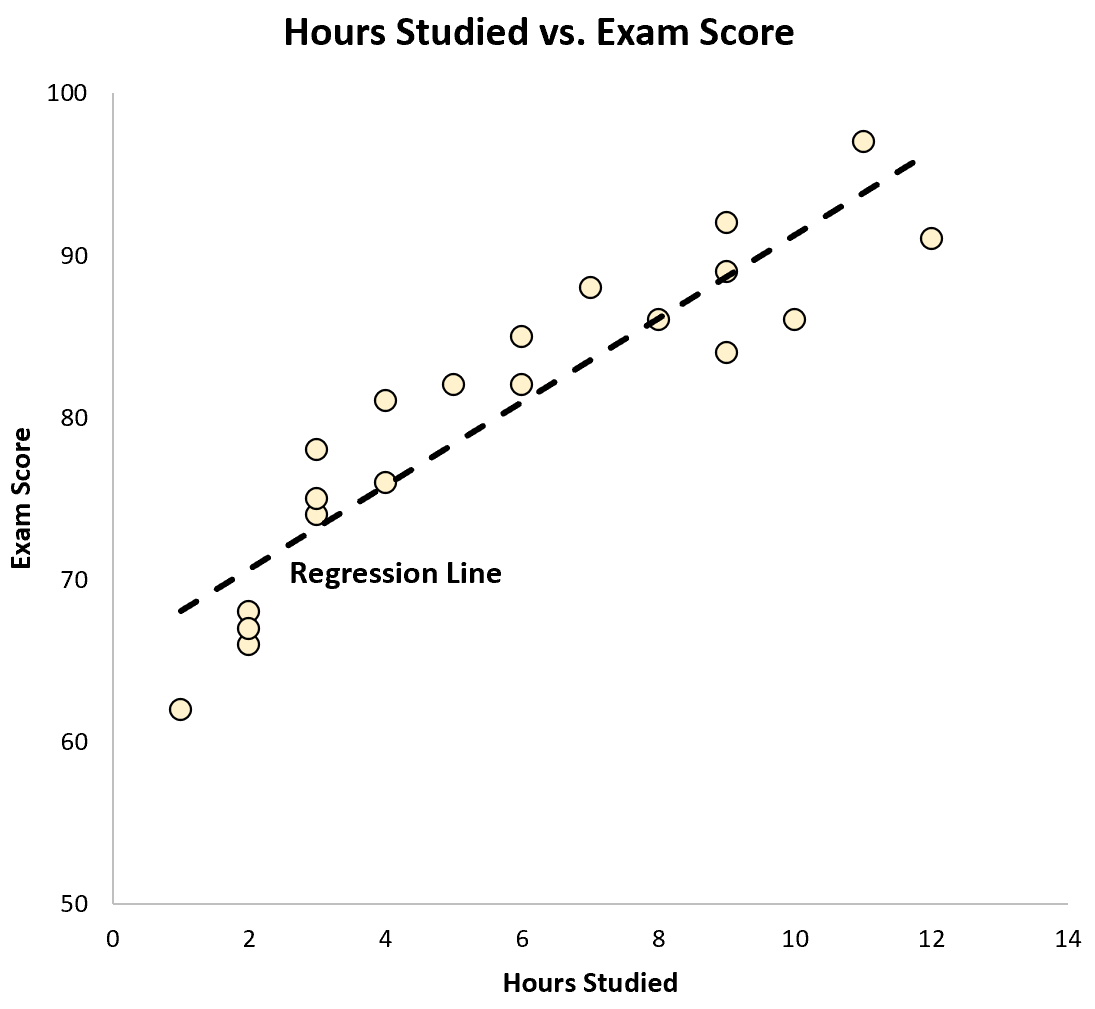
Ми бачимо, що лінія регресії досить добре «вписується» в дані.

Нагадаємо, раніше кореляція між цими двома змінними становила r = 0,915 . Виявляється, ми можемо звести це значення в квадрат і отримати число, яке називається «r у квадраті», яке описує загальну частку дисперсії у змінній відповіді, яку можна пояснити змінною предиктора.

У цьому прикладі r ² = 0,915 ² = 0,837 . Це означає, що 83,7% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.

Кореляція проти регресії: подібності та відмінності

Ось короткий виклад подібностей і відмінностей між кореляцією та регресією:

Подібності:

• Обидва параметри кількісно визначають напрямок зв’язку між двома змінними.
• Обидва параметри кількісно визначають силу зв’язку між двома змінними.

відмінності:

• Регресія здатна показати причинно-наслідковий зв’язок між двома змінними. Кореляція цього не робить.
• Регресія може використовувати рівняння для прогнозування значення однієї змінної на основі значення іншої змінної. Кореляція цього не робить.
• Регресія використовує рівняння для кількісного визначення зв’язку між двома змінними. Кореляція використовує одне число.

Додаткові ресурси

Наступні навчальні посібники пропонують більш глибокі пояснення тем, розглянутих у цій статті.

Вступ до коефіцієнта кореляції Пірсона
Вступ до простої лінійної регресії
Простий калькулятор лінійної регресії
Що таке хороше значення R-квадрат?