Тест брауна–форсайта в r: покроковий приклад

Односторонній дисперсійний аналіз використовується для визначення того, чи існує значна різниця між середніми значеннями трьох або більше незалежних груп.

Одне з припущень одностороннього дисперсійного аналізу полягає в тому, що дисперсії популяцій, з яких відбираються зразки, рівні.

Одним із найпоширеніших способів перевірити це є використання тесту Брауна-Форсайта , який є статистичним тестом, який використовує такі припущення :

• H ₀ : дисперсії між популяціями рівні.
• H _A : Відмінності між популяціями неоднакові.

Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), тоді ми відхиляємо нульову гіпотезу та робимо висновок, що дисперсії не однакові між різними сукупностями.

Цей підручник надає покроковий приклад того, як виконати тест Брауна-Форсайта в R.

Крок 1: Введіть дані

Припустімо, ми хотіли б знати, чи призводять три різні програми тренувань до різних рівнів втрати ваги.

Щоб перевірити це, ми набираємо 90 людей і випадковим чином призначаємо 30 для використання кожної програми. Потім ми вимірюємо втрату ваги кожної людини через один місяць.

Наступний набір даних містить інформацію про кількість втраченої ваги за кожною програмою:

 #make this example reproducible
set.seed(0)

#create data frame
data <- data.frame(program = as . factor ( rep (c(" A ", " B ", " C "), each = 30)),
                   weight_loss = c( runif (30, 0, 3),
                                   runif (30, 0, 5),
                                   runif (30, 1, 7)))

#view first six rows of data frame
head(data)

# program weight_loss
#1 A 2.6900916
#2 A 0.7965260
#3 A 1.1163717
#4 A 1.7185601
#5 A 2.7246234
#6 A 0.6050458

Крок 2: підсумуйте та візуалізуйте дані

Перед виконанням тесту Брауна-Форсайта ми можемо створити коробкові діаграми, щоб візуалізувати дисперсію втрати ваги для кожної групи:

 boxplot(weight_loss ~ program, data = data)

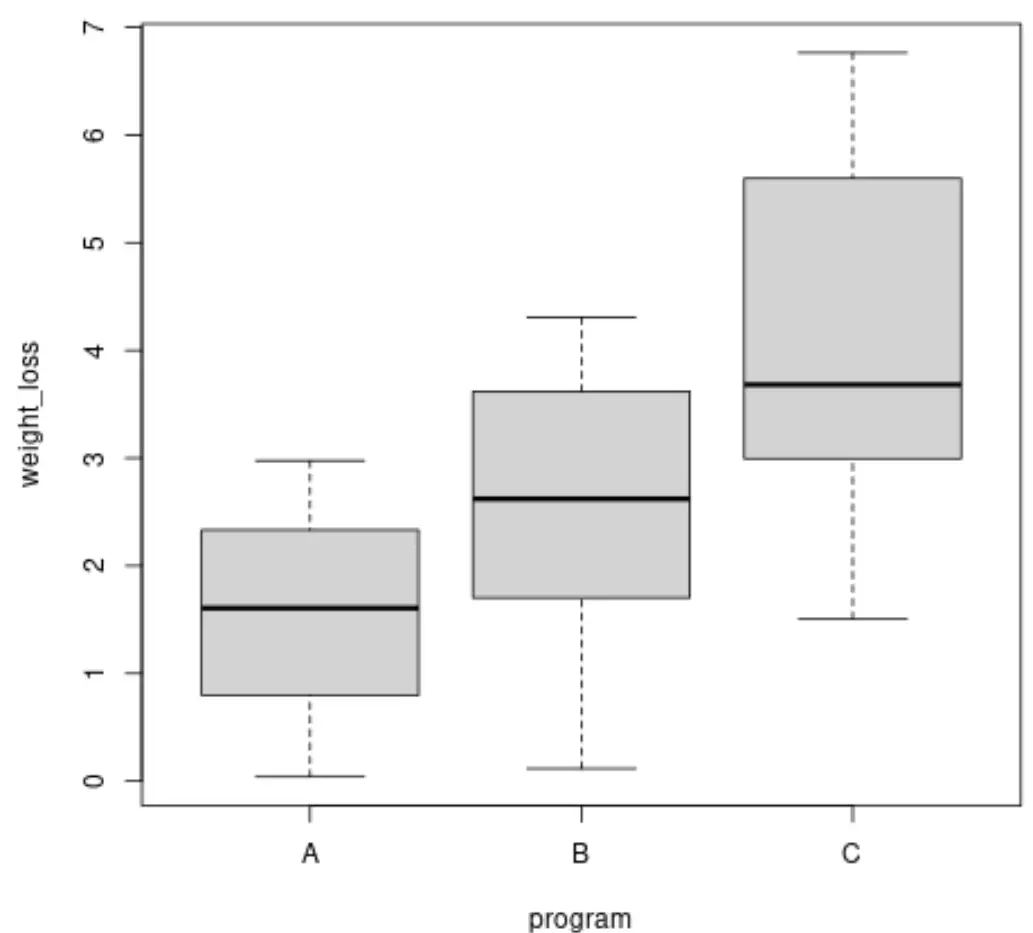
Ми також можемо розрахувати дисперсію втрати ваги в кожній групі:

 #load dplyr package
library (dplyr)

#calculate variance of weight loss by group
data %>%
group_by (program) %>%
  summarize (var=var(weight_loss))

# A tibble: 3 x 2
  program var
     
1 A 0.819
2 B 1.53 
3 C 2.46

Ми бачимо, що дисперсії між групами відрізняються, але щоб визначити, чи ці відмінності є статистично значущими , ми можемо виконати тест Брауна-Форсайта.

Крок 3: Виконайте тест Брауна-Форсайта

Щоб виконати тест Брауна-Форсайта в R, ми можемо використати функцію bf.test() з пакету onewaytests :

 #load onewaytests package
library (onewaytests)

#perform Brown-Forsythe test
bf.test(weight_loss ~ program, data = data)

  Brown-Forsythe Test (alpha = 0.05) 
-------------------------------------------------- ----------- 
  data: weight_loss and program 

  statistic: 30.83304 
  num df: 2 
  name df: 74.0272 
  p.value: 1.816529e-10 

  Result: Difference is statistically significant. 
-------------------------------------------------- -----------

P-значення тесту виявляється меншим за 0,000, і, як показує результат, відмінності в дисперсіях між трьома групами є статистично значущими.

Наступні кроки

Якщо ви не можете відхилити нульову гіпотезу тесту Брауна-Форсайта, ви можете виконати односторонній дисперсійний аналіз даних.

Однак якщо відкинути нульову гіпотезу, це означає, що припущення про рівність дисперсій порушується. У цьому випадку у вас є два варіанти:

1. Все одно виконайте односторонній дисперсійний аналіз.

Виявляється, односторонній дисперсійний аналіз фактично стійкий до нерівних дисперсій, якщо найбільша дисперсія не перевищує найменшу дисперсію в 4 рази.

На кроці 2 прикладу вище ми виявили, що найменша дисперсія становила 0,819, а найбільша – 2,46. Отже, відношення найбільшої дисперсії до найменшої становить 2,46/0,819 = 3,003 .

Оскільки це значення менше 4, ми могли б просто виконати односторонній дисперсійний аналіз.

2. Виконайте тест Крускала-Уолліса

Якщо відношення найбільшої дисперсії до найменшої дисперсії перевищує 4, замість цього можна вибрати тест Краскела-Уолліса . Це вважається непараметричним еквівалентом одностороннього дисперсійного аналізу.

Ви можете знайти покроковий приклад тесту Крускала-Уолліса в R тут .