R-кратне або r-квадрат: у чому різниця?

Коли ви підбираєте модель регресії за допомогою більшості статистичних програм, ви часто помічаєте в результаті такі два значення:

Множинний R: коефіцієнт множинної кореляції між трьома або більше змінними.

R-квадрат: обчислюється як (множинне R) ² і представляє частку дисперсії у змінній відповіді регресійної моделі, яку можна пояснити змінними предикторів. Це значення змінюється від 0 до 1.

На практиці нас часто цікавить значення R-квадрат, оскільки воно говорить нам, наскільки корисними є змінні предикторів у передбаченні значення змінної відповіді.

Однак кожного разу, коли ми додаємо нову змінну предиктора до моделі, R-квадрат гарантовано зростатиме, навіть якщо змінна предиктора не є корисною.

Скоригований R-квадрат – це модифікована версія R-квадрату, яка коригує кількість предикторів у регресійній моделі. Він розраховується таким чином:

Скоригований R ² = 1 – [(1-R ² )*(n-1)/(nk-1)]

золото:

• R ² : R ² моделі
• n : кількість спостережень
• k : кількість змінних предиктора

Оскільки R-квадрат завжди збільшується, коли ви додаєте більше предикторів до моделі, скоригований R-квадрат може служити показником, який повідомляє вам, наскільки корисна модель, скоригована на основі кількості предикторів у моделі .

Щоб краще зрозуміти кожен із цих термінів, розглянемо наступний приклад.

Приклад: кілька R, R-квадрат і скоригований R-квадрат

Припустімо, що ми маємо наступний набір даних, який містить такі три змінні для 12 різних студентів:

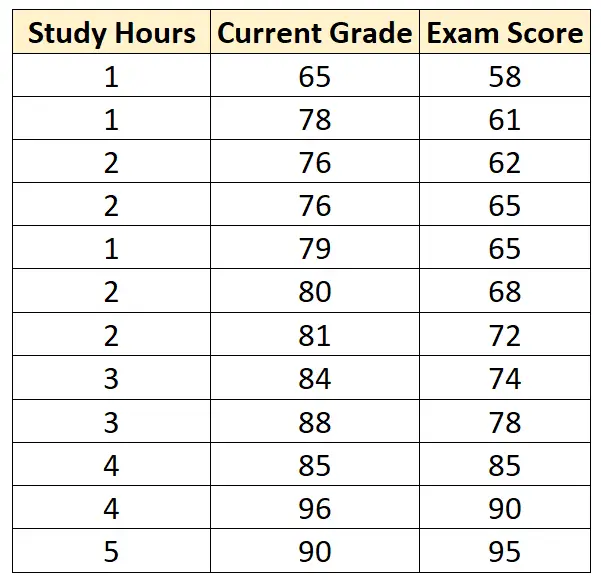
Припустімо, що ми підбираємо модель множинної лінійної регресії, використовуючи навчальні години та поточну оцінку як змінні-прогнози та оцінку іспиту як змінну відповіді, і отримуємо такий результат:

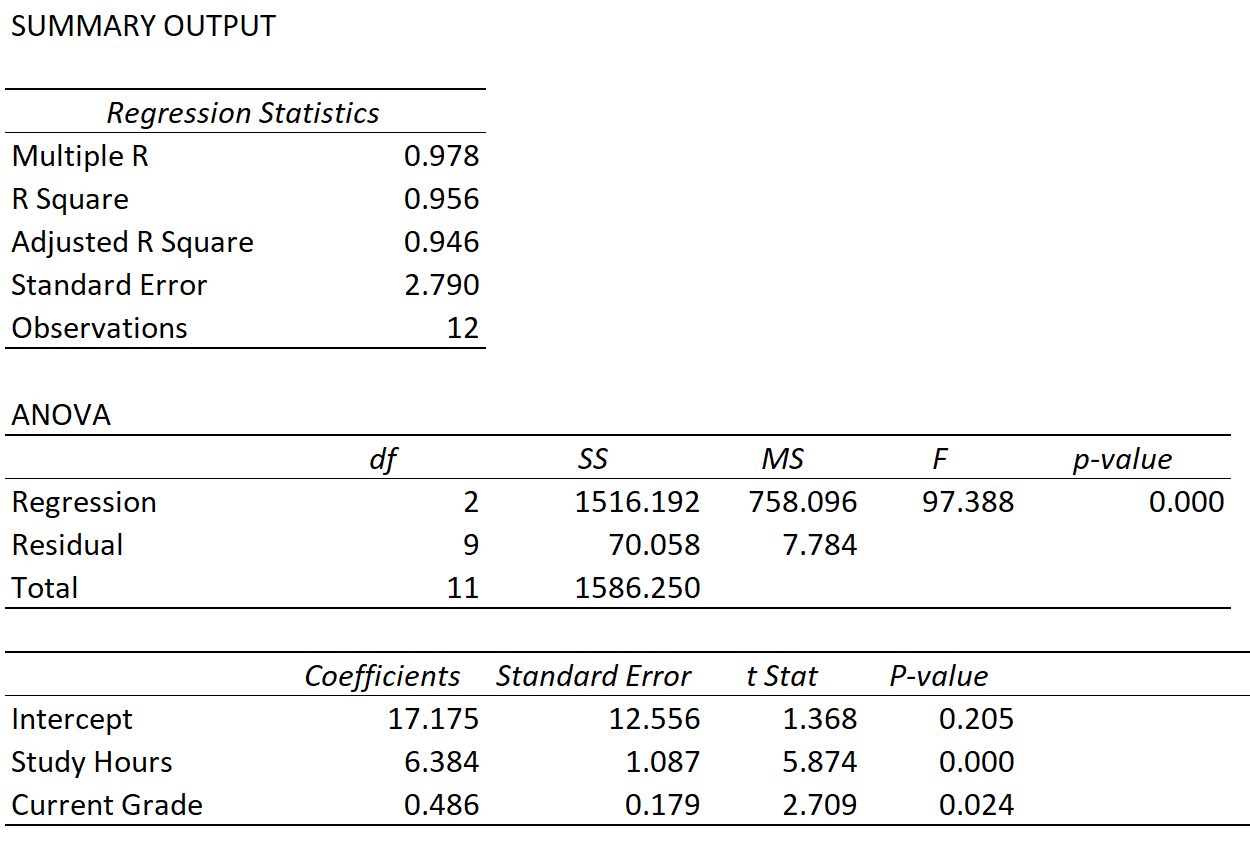
Ми можемо спостерігати значення наступних трьох показників:

Кратний R: 0,978 . Це являє собою множинну кореляцію між змінною відповіді та двома змінними предиктора.

Квадрат R: 0,956 . Це обчислюється як (кратне R) ² = (0,978) ² = 0,956. Це говорить нам про те, що 95,6% варіації оцінок на іспитах можна пояснити кількістю годин, які студенти витратили на навчання, і їх поточною оцінкою за курс.

Скоригований R-квадрат: 0,946 . Це розраховується таким чином:

Скоригований R ² = 1 – [(1-R ² )*(n-1)/(nk-1)] = 1 – [(1-,956)*(12-1)/(12-2-1) ] = 0,946.

Це значення R-квадрат, скориговане на кількість змінних предиктора в моделі .

Ця міра буде корисною, якщо, наприклад, ми підберемо іншу модель регресії з 10 предикторами та виявимо, що скоригований R-квадрат цієї моделі становить 0,88 . Це означатиме, що модель регресії лише з двома предикторами є кращою, оскільки вона має вищий скоригований R-квадрат.

Додаткові ресурси

Вступ до множинної лінійної регресії
Що таке хороше значення R-квадрат?