Що таке криві густини? (пояснення та приклади)

Крива щільності — це крива на графіку, яка представляє розподіл значень у наборі даних. Це корисно з трьох причин:

1. Крива щільності дає нам гарне уявлення про «форму» розподілу, включно з тим, чи має розподіл один або кілька «піків» значень частоти та чи є розподіл перекошеним вліво. або праворуч. ПРАВИЛЬНО. .

2. Крива щільності дозволяє нам візуально побачити, де співвідносяться середнє та медіана розподілу.

3. Крива щільності дозволяє нам візуально побачити, який відсоток спостережень у наборі даних знаходиться між різними значеннями.

Найбільш відомою кривою густини є дзвоноподібна крива, яка представляє нормальний розподіл .

Щоб краще зрозуміти криві щільності, розглянемо наступний приклад.

Приклад: створення та інтерпретація кривої щільності

Скажімо, у нас є такий набір даних, який показує висоту 20 різних рослин (у дюймах) у певному полі:

4, 5, 5, 6, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 9, 2, 2

Якби ми створили просту гістограму для відображення відносних частот кожного значення, вона виглядала б так:

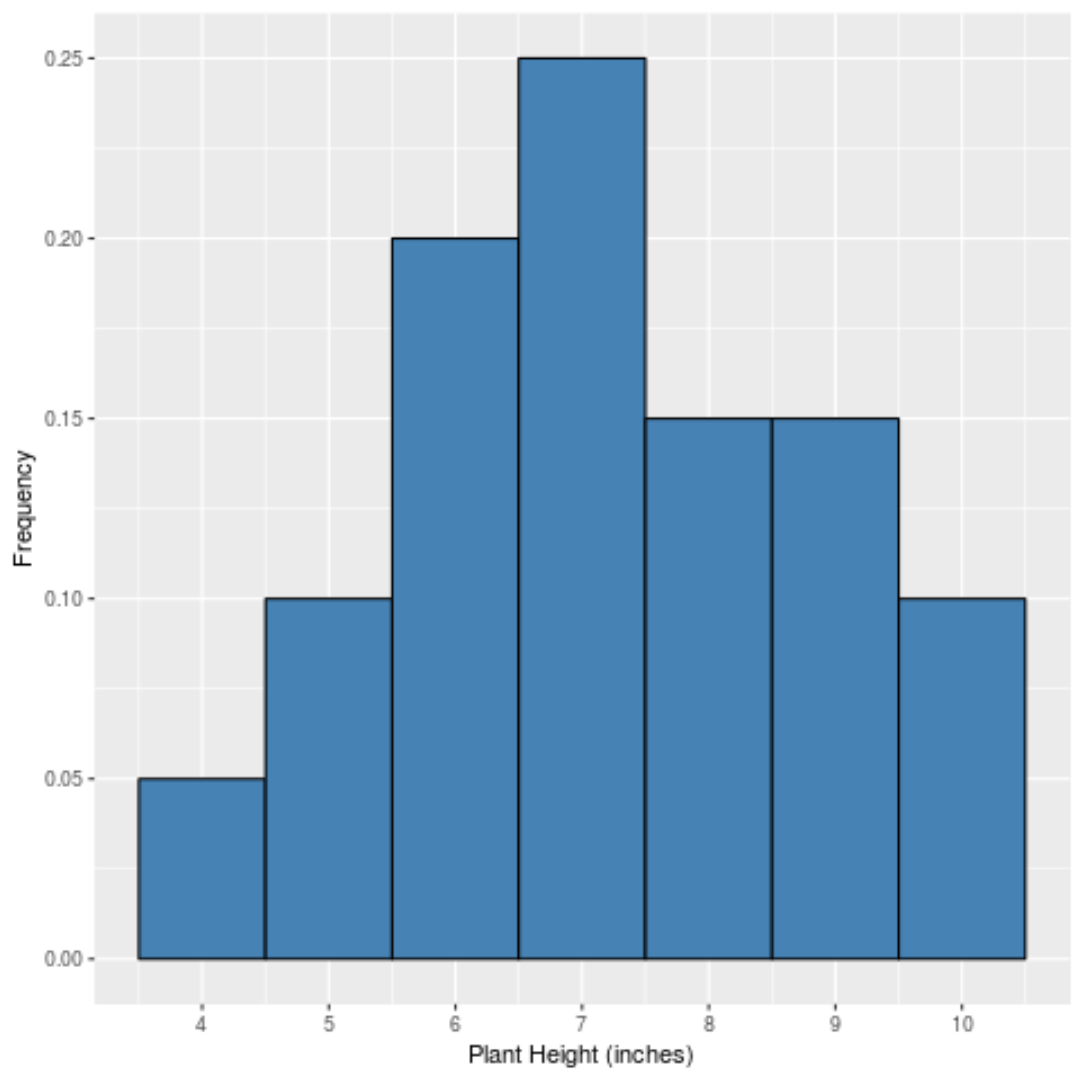
На осі х показано значення даних, а на осі у – відносна частота (наприклад, значення «7» з’являється 5 разів із 20 загальних значень у наборі даних, тому воно має відносну частоту 25% або 0,25 .

І якби ми створили криву щільності , щоб зафіксувати «форму» цього розподілу, вона виглядала б так:

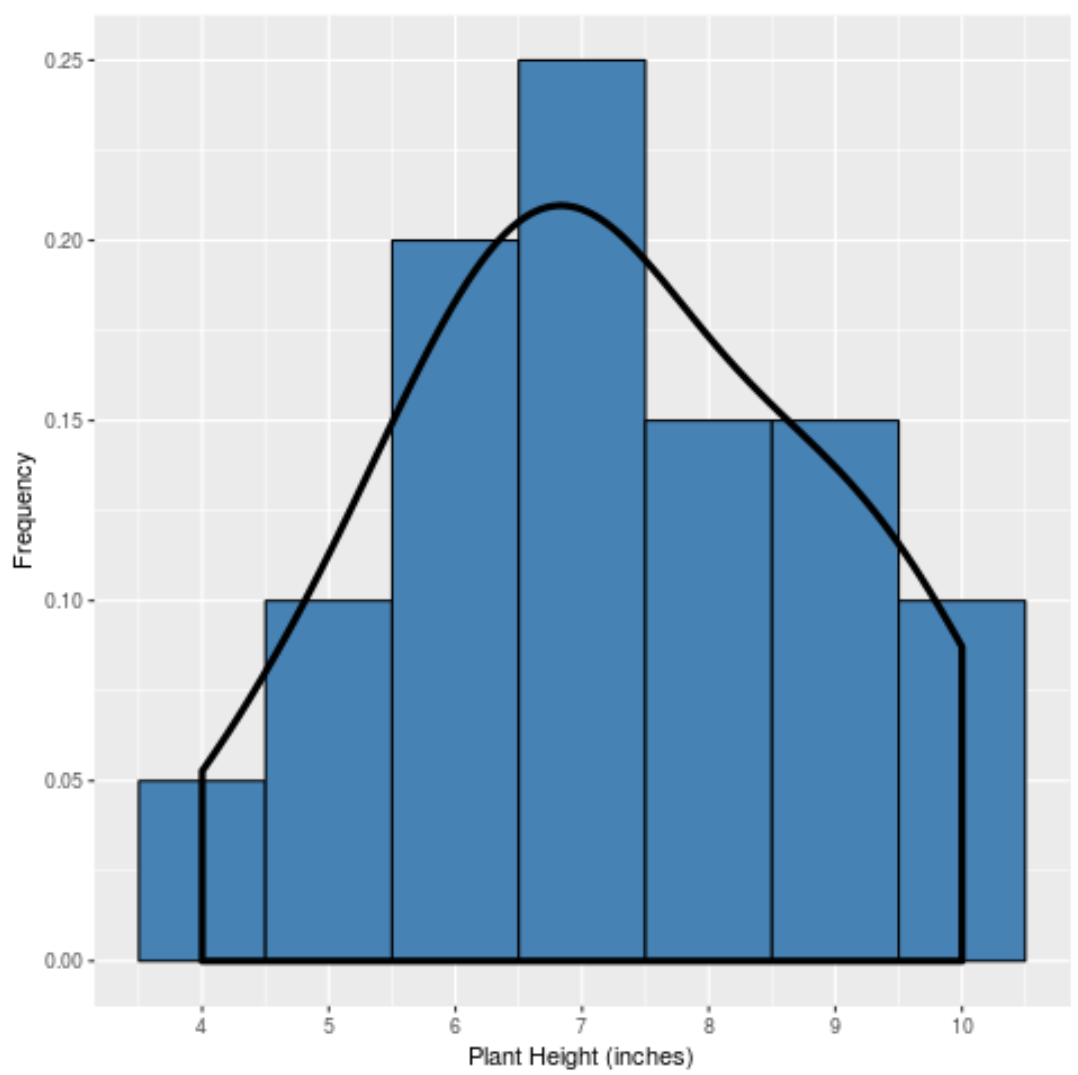
Крива найвища поблизу центру розподілу, тому що саме там міститься більшість значень. Він також є найнижчим біля кінців розподілу, оскільки менша кількість рослин приймає ці значення (наприклад, висота 4 дюйми або 10 дюймів).

Як інтерпретувати криві щільності

Криві щільності бувають будь-яких форм і розмірів, і вони дозволяють нам отримати швидке візуальне розуміння розподілу значень у певному наборі даних. Вони особливо корисні, щоб допомогти нам візуалізувати:

1. Асиметрія

Асиметрія – це спосіб опису симетрії розподілу. Криві щільності дозволяють нам швидко побачити, чи нахилений графік вліво, вправо чи без нахилу:

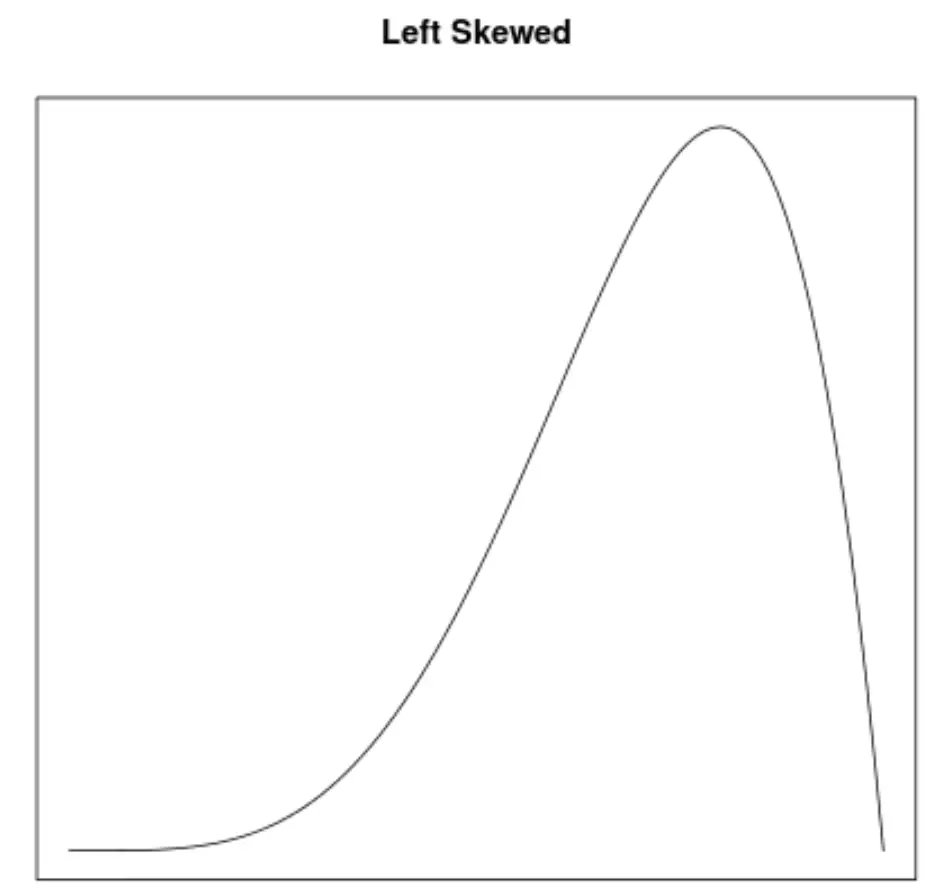
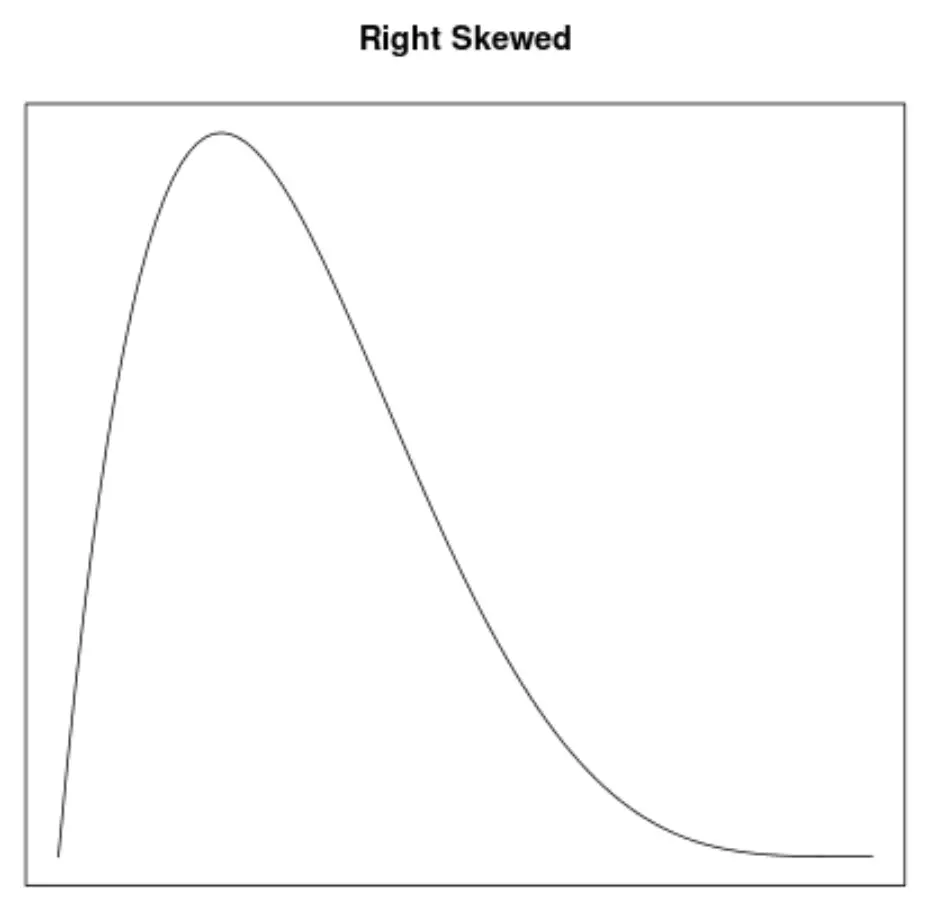
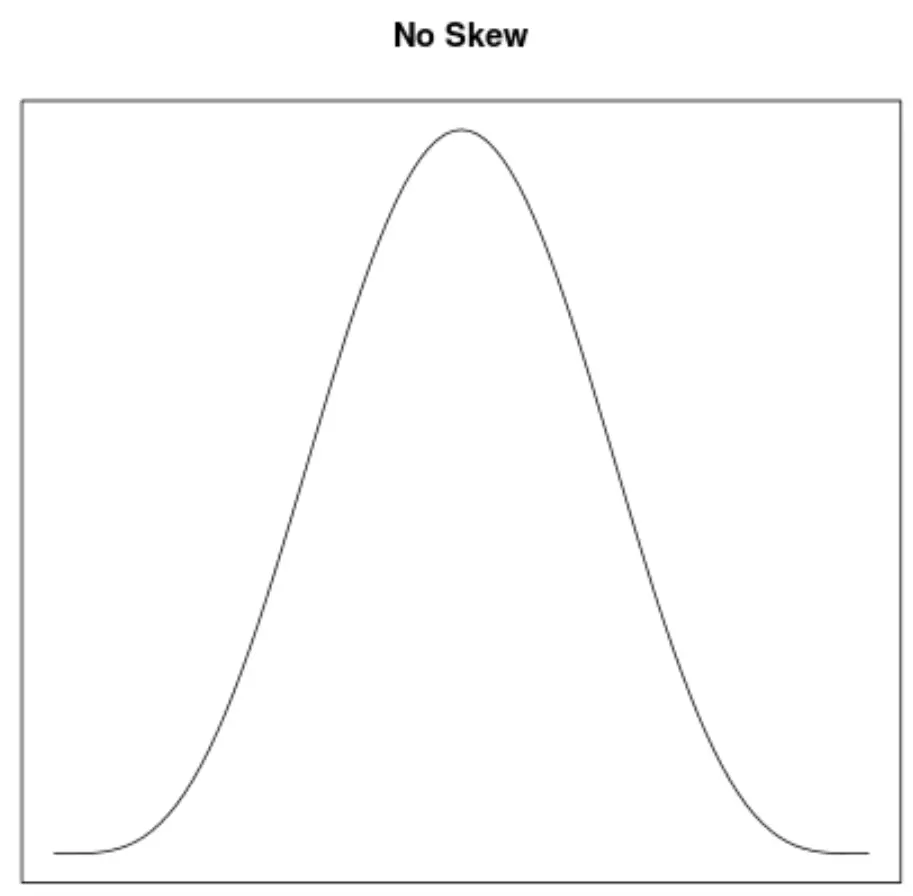
2. Розташування середнього та медіани

На основі асиметрії кривої щільності ми можемо швидко визначити, чи є середнє чи медіана більшим у даному розподілі. Особливо:

• Якщо крива щільності залишається асиметричною , то середнє значення нижче за медіану.
• Якщо крива щільності зміщена вправо , то середнє значення більше медіани.
• Якщо крива щільності не має асиметрії , то середнє дорівнює медіані.

3. Кількість піків

Криві щільності також дозволяють нам швидко побачити, скільки «піків» є в даному розподілі. У кожному з наведених вище прикладів розподіли мали лише один пік, тому ми б описали ці розподіли як унімодальні .

Однак деякі розподіли можуть мати два піки, які ми називаємо бімодальними розподілами . У рідкісних випадках ми також можемо мати мультимодальні розподіли з двома або більше піками.

Просто створивши криву щільності для даного набору даних, ми можемо швидко побачити, скільки піків у розподілі.

Властивості кривих густини

Криві густини мають такі властивості:

• Площа під кривою завжди дорівнює 100%.
• Крива ніколи не буде опускатися нижче осі х.

Майте на увазі ці два факти, створюючи або інтерпретуючи криві щільності для різних розподілів.

Додаткові ресурси

Введення в гістограми відносної частоти
Як створити дзвоноподібну криву в Excel
Як створити дзвоноподібну криву в Python