Як виконати регресію loess у r (з прикладом)

Регресія LOESS , яку іноді називають локальною регресією, — це метод, який використовує локальне коригування для підгонки моделі регресії до набору даних.

Наступний покроковий приклад показує, як виконати регресію LOESS у R.

Крок 1: Створіть дані

Спочатку давайте створимо наступний кадр даних у R:

 #view DataFrame
df <- data. frame (x=c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14),
                 y=c(1, 4, 7, 13, 19, 24, 20, 15, 13, 11, 15, 18, 22, 27))

#view first six rows of data frame
head(df)

  xy
1 1 1
2 2 4
3 3 7
4 4 13
5 5 19
6 6 24

Крок 2. Підберіть кілька моделей регресії LOESS

Ми можемо використовувати функцію loess() , щоб підібрати кілька моделей регресії LOESS до цього набору даних, використовуючи різні значення для параметра span :

 #fit several LOESS regression models to dataset
loess50 <- loess(y ~ x, data=df, span= .5 )
smooth50 <- predict(loess50) 

loess75 <- loess(y ~ x, data=df, span= .75 )
smooth75 <- predict(loess75) 

loess90 <- loess(y ~ x, data=df, span= .9 )
smooth90 <- predict(loess90) 

#create scatterplot with each regression line overlaid
plot(df$x, df$y, pch= 19 , main=' Loess Regression Models ')
lines(smooth50, x=df$x, col=' red ')
lines(smooth75, x=df$x, col=' purple ')
lines(smooth90, x=df$x, col=' blue ')
legend(' bottomright ', legend=c(' .5 ', ' .75 ', ' .9 '),
        col=c(' red ', ' purple ', ' blue '), pch= 19 , title=' Smoothing Span ')

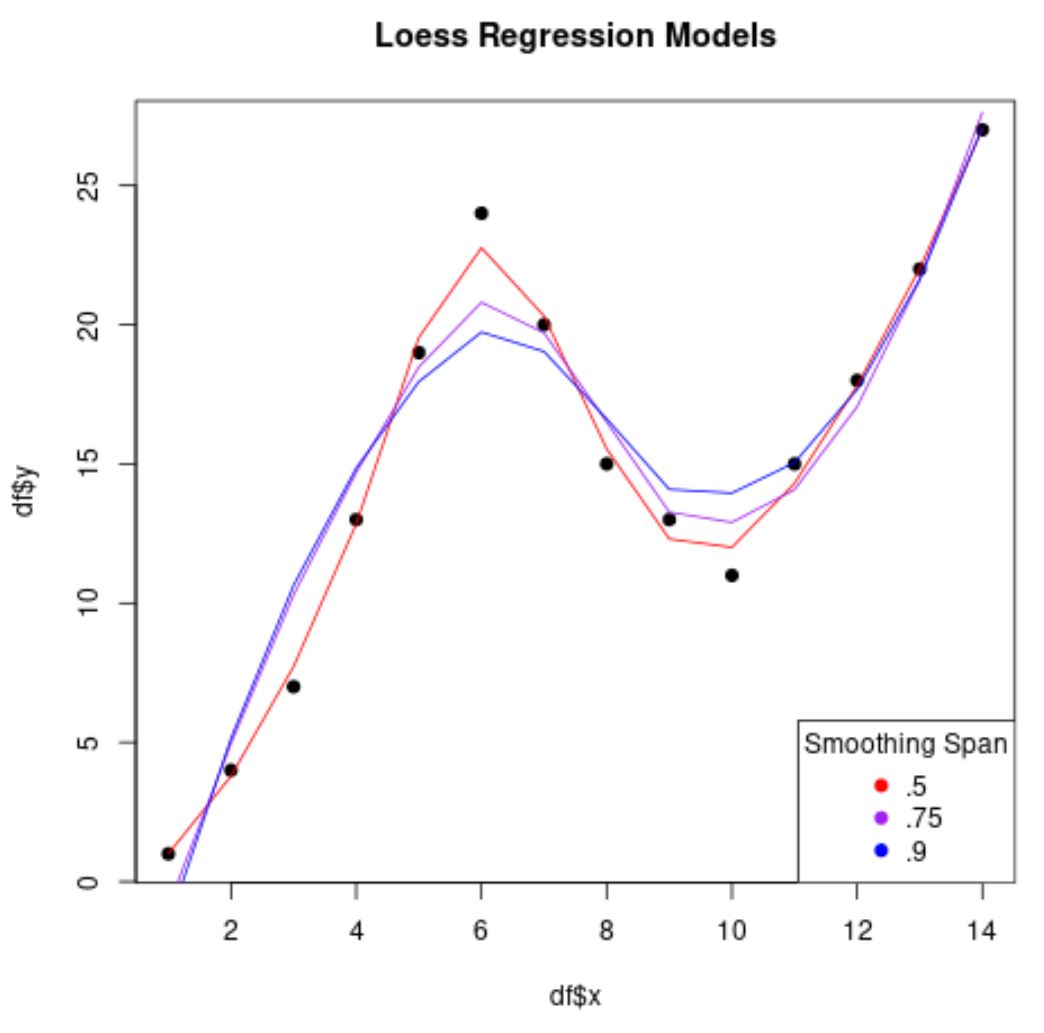
Зауважте, що чим менше значення, яке ми використовуємо для span , тим менш «гладкою» буде регресійна модель і тим більше вона намагатиметься підібрати точки даних.

Крок 3. Використовуйте перехресну перевірку K-кратного згортання, щоб знайти найкращу модель

Щоб знайти оптимальне значення екстента для використання, ми можемо виконати k-кратну перехресну перевірку за допомогою функцій у пакеті каретки :

 library (caret)

#define k-fold cross validation method
ctrl <- trainControl(method = " cv ", number = 5 )
grid <- expand. grid (span = seq( 0.5 , 0.9 , len = 5 ), degree = 1 )

#perform cross-validation using smoothing spans ranging from 0.5 to 0.9
model <- train(y ~ x, data = df, method = " gamLoess ", tuneGrid=grid, trControl = ctrl)

#print results of k-fold cross-validation
print (model)

14 samples
 1 predictor

No pre-processing
Resampling: Cross-Validated (5 fold) 
Summary of sample sizes: 12, 11, 11, 11, 11 
Resampling results across tuning parameters:

  span RMSE Rsquared MAE      
  0.5 10.148315 0.9570137 6.467066
  0.6 7.854113 0.9350278 5.343473
  0.7 6.113610 0.8150066 4.769545
  0.8 17.814105 0.8202561 11.875943
  0.9 26.705626 0.7384931 17.304833

Tuning parameter 'degree' was held constant at a value of 1
RMSE was used to select the optimal model using the smallest value.
The final values used for the model were span = 0.7 and degree = 1.

Ми бачимо, що значення діапазону , яке дало найменше значення середньоквадратичної помилки (RMSE), становить 0,7 .

Отже, для нашої остаточної регресійної моделі LOESS ми вирішили використовувати значення 0,7 для аргументу span у функції loess() .

Додаткові ресурси

У наступних посібниках надається додаткова інформація про моделі регресії в R:

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати логістичну регресію в R
Як виконати квантильну регресію в R
Як виконати зважену регресію в R