Логанормальний розподіл

за Редакція 3 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке логнормальний розподіл у статистиці. Отже, ви дізнаєтеся, якими властивостями володіє логарифмічний нормальний розподіл і графік цього типу розподілу ймовірностей.

Що таке логнормальний розподіл?

Логарифмічний нормальний розподіл або логарифмічний нормальний розподіл — це розподіл ймовірностей, який визначає випадкову величину, чий логарифм відповідає нормальному розподілу.

Отже, якщо змінна X має нормальний розподіл, то експоненціальна функція e ^x має логнормальний розподіл.

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Зауважте, що логарифмічний нормальний розподіл можна використовувати лише тоді, коли значення змінної додатні, оскільки логарифм — це функція, яка приймає лише один додатний аргумент.

Серед різних застосувань логнормального розподілу в статистиці ми виділяємо використання цього розподілу для аналізу фінансових інвестицій і проведення аналізу надійності.

Логнормальний розподіл також відомий як розподіл Тіно , іноді також записується як логарифмічний нормальний розподіл або логарифмічний нормальний розподіл .

Графік логарифмічного нормального розподілу

Тепер, коли ми знаємо визначення логарифмічного нормального розподілу, ми побачимо в цьому розділі, як змінюється графічне представлення логарифмічного нормального розподілу залежно від значень його середнього арифметичного та стандартного відхилення.

Графік функції щільності логарифмічного нормального розподілу має такий вигляд:

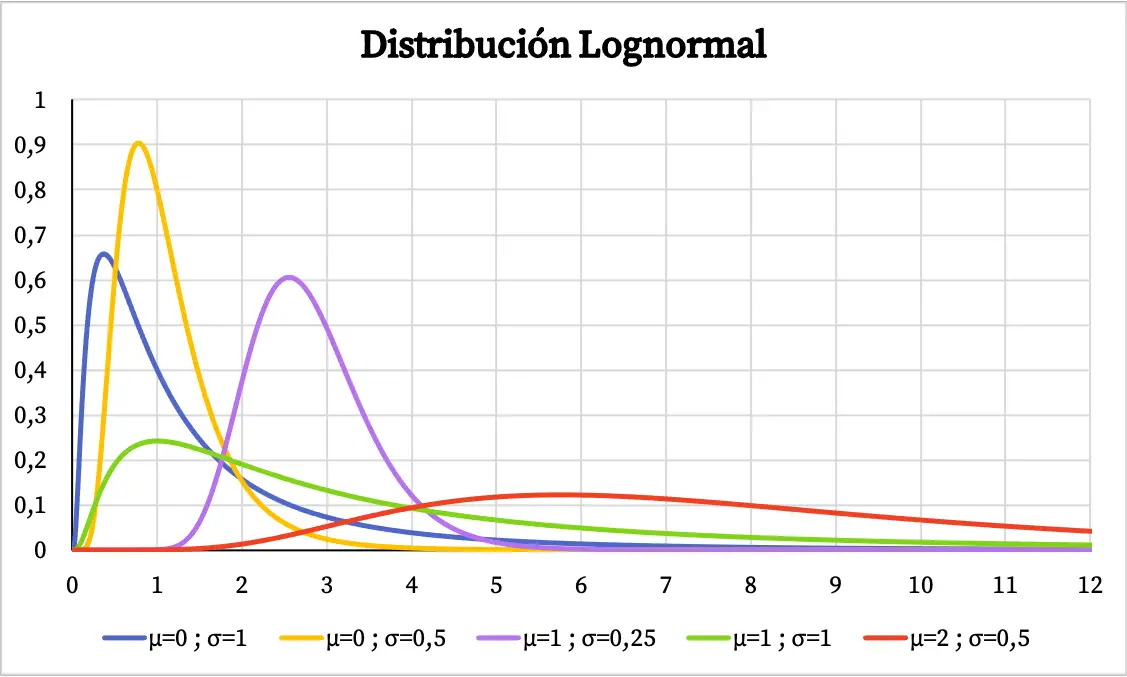
З іншого боку, кумулятивний імовірнісний графік логарифмічного нормального розподілу виглядає наступним чином:

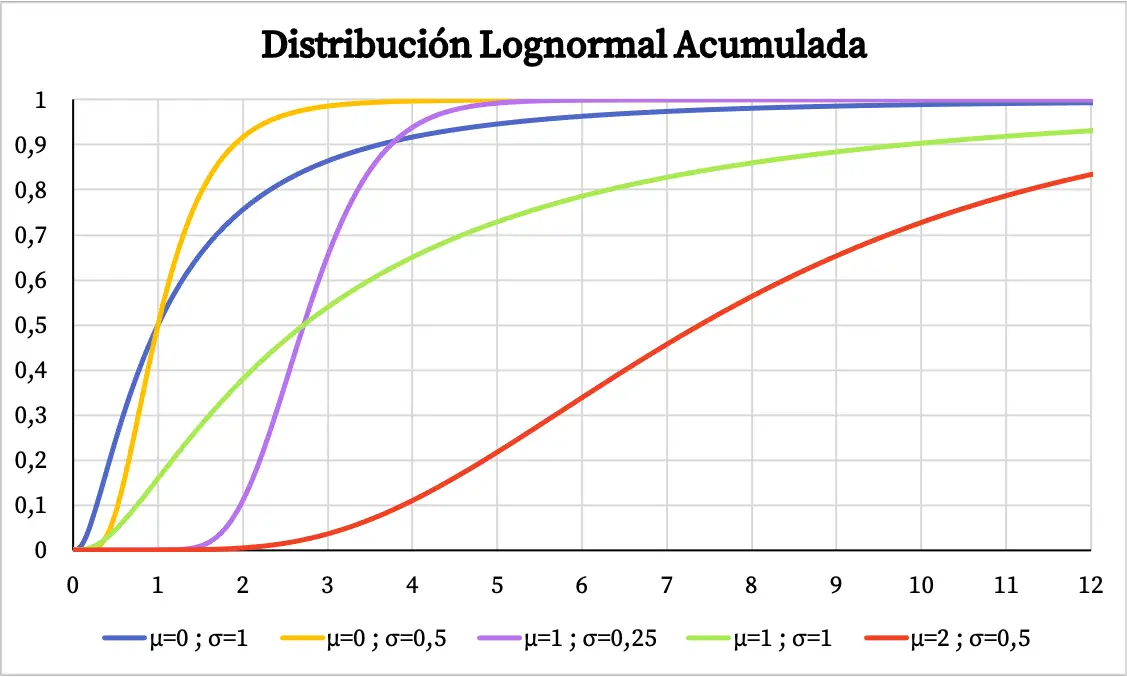
графік кумулятивної ймовірності логарифмічного нормального розподілу

Характеристики логнормального розподілу

Логнормальний розподіл має такі характеристики:

Логнормальний розподіл визначається значенням двох параметрів, його середнім арифметичним μ і його дисперсією σ ² .

$X\sim \text{Lognormal}(\mu,\sigma^2)$

Область логарифмічного нормального розподілу складається з додатних дійсних чисел, оскільки логарифм не приймає від’ємних або нульових значень.

$x\in (0,+\infty)$

Математичне сподівання логарифмічного нормального розподілу дорівнює числу e, піднесеному до суми середнього плюс дисперсія, поділена на два.

$\displaystyle E[X]=e^{\mu+\frac{\sigma^2}{2}}$

З іншого боку, дисперсію логарифмічного нормального розподілу можна обчислити за таким виразом:

$Var(X)=\left(e^{\sigma^2}-1\right)\cdot e^{2\mu+\sigma^2$

Режим логнормального розподілу еквівалентний числу e, піднесеному до середнього значення розподілу.

$Mo=e^\mu$

Коефіцієнт асиметрії логарифмічного нормального розподілу можна визначити за такою формулою:

$\displaystyle A=\left(e^{\sigma^2}+2\right)\cdot\sqrt{e^{\sigma^2}-1}$

Формула для функції густини логарифмічного нормального розподілу має вигляд:

$\displaystyle P[X=x]=\frac{1}{\sigma \cdot x\cdot \sqrt{2 \pi}}\cdot \exp\left(-\frac{(\ln x-\mu)^2}{2\sigma^2}\right)$

Формула для кумулятивної функції ймовірності логнормального розподілу має вигляд:

$\displaystyle P[X\leq x]=\Phi\left(\frac{\ln x-\mu}{\sigma}\right)$

золото

$\Phi$

є кумулятивною функцією ймовірності стандартного нормального розподілу .

Середнє арифметичне логарифмічного нормального розподілу більше, ніж значення його медіани.

$\mu > Me” title=”Rendered by QuickLaTeX.com” height=”16″ width=”61″ style=”vertical-align: -4px;”></p></p> </div>  <div class=$

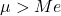
Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше

Що таке логнормальний розподіл?

Графік логарифмічного нормального розподілу

Характеристики логнормального розподілу

Про автора

Редакція

Додати коментар