Логарифмічна регресія в r (покроково)

Логарифмічна регресія — це тип регресії, який використовується для моделювання ситуацій, у яких зростання або спад спочатку швидко прискорюється, а потім сповільнюється з часом.

Наприклад, наступний графік показує приклад логарифмічного розпаду:

Для такого типу ситуації зв’язок між змінною-прогностикою та змінною відповіді можна добре змоделювати за допомогою логарифмічної регресії.

Рівняння для моделі логарифмічної регресії має такий вигляд:

y = a + b*ln(x)

золото:

• y: змінна відповіді
• x: передбачувана змінна
• a, b: коефіцієнти регресії, які описують зв’язок між x і y

Наступний покроковий приклад показує, як виконати логарифмічну регресію в R.

Крок 1: Створіть дані

Спочатку давайте створимо фальшиві дані для двох змінних: x і y :

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

Крок 2: Візуалізуйте дані

Далі створимо швидку діаграму розсіювання, щоб візуалізувати зв’язок між x і y :

 plot(x, y) 

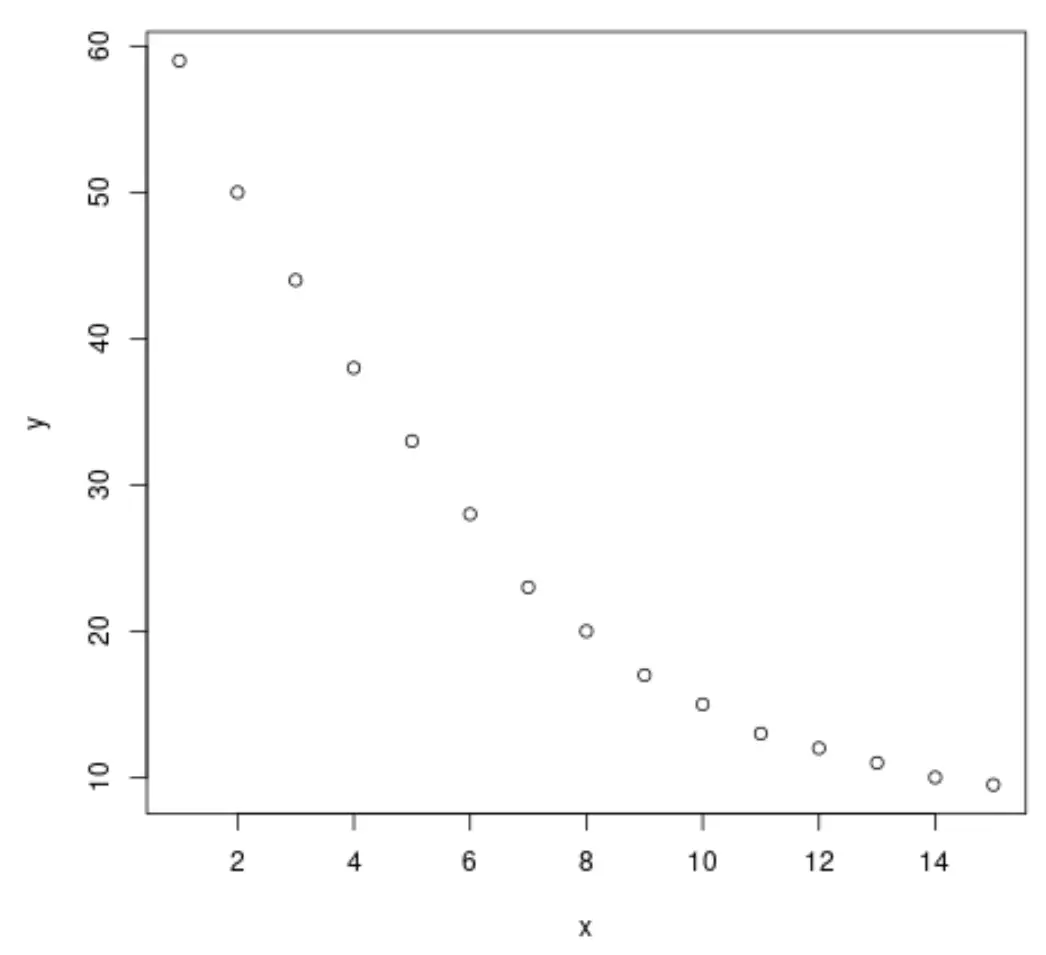
З графіка ми бачимо, що між двома змінними існує чітка логарифмічна схема спаду. Значення змінної відповіді, y , спочатку швидко зменшується, а потім сповільнюється з часом.

Тому здається розумним підібрати рівняння логарифмічної регресії для опису зв’язку між змінними.

Крок 3: Підберіть модель логарифмічної регресії

Далі ми використаємо функцію lm() , щоб підібрати модель логарифмічної регресії, використовуючи натуральний логарифм x як змінну-прогноз і y як змінну відповіді.

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

Загальне F-значення моделі становить 828,2, а відповідне значення p надзвичайно низьке (3,702e-13), що вказує на те, що модель в цілому корисна.

Використовуючи коефіцієнти з вихідної таблиці, ми можемо побачити, що підігнане рівняння логарифмічної регресії таке:

y = 63,0686 – 20,1987 * ln(x)

Ми можемо використати це рівняння для прогнозування змінної відповіді y на основі значення змінної предиктора x . Наприклад, якщо x = 12, ми передбачимо, що y дорівнюватиме 12,87 :

y = 63,0686 – 20,1987 * ln(12) = 12,87

Бонус: не соромтеся використовувати цей онлайн-калькулятор логарифмічної регресії, щоб автоматично обчислити рівняння логарифмічної регресії для заданого предиктора та змінної відповіді.

Крок 4: Візуалізуйте модель логарифмічної регресії

Нарешті, ми можемо створити швидкий графік, щоб візуалізувати, наскільки модель логарифмічної регресії відповідає даним:

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

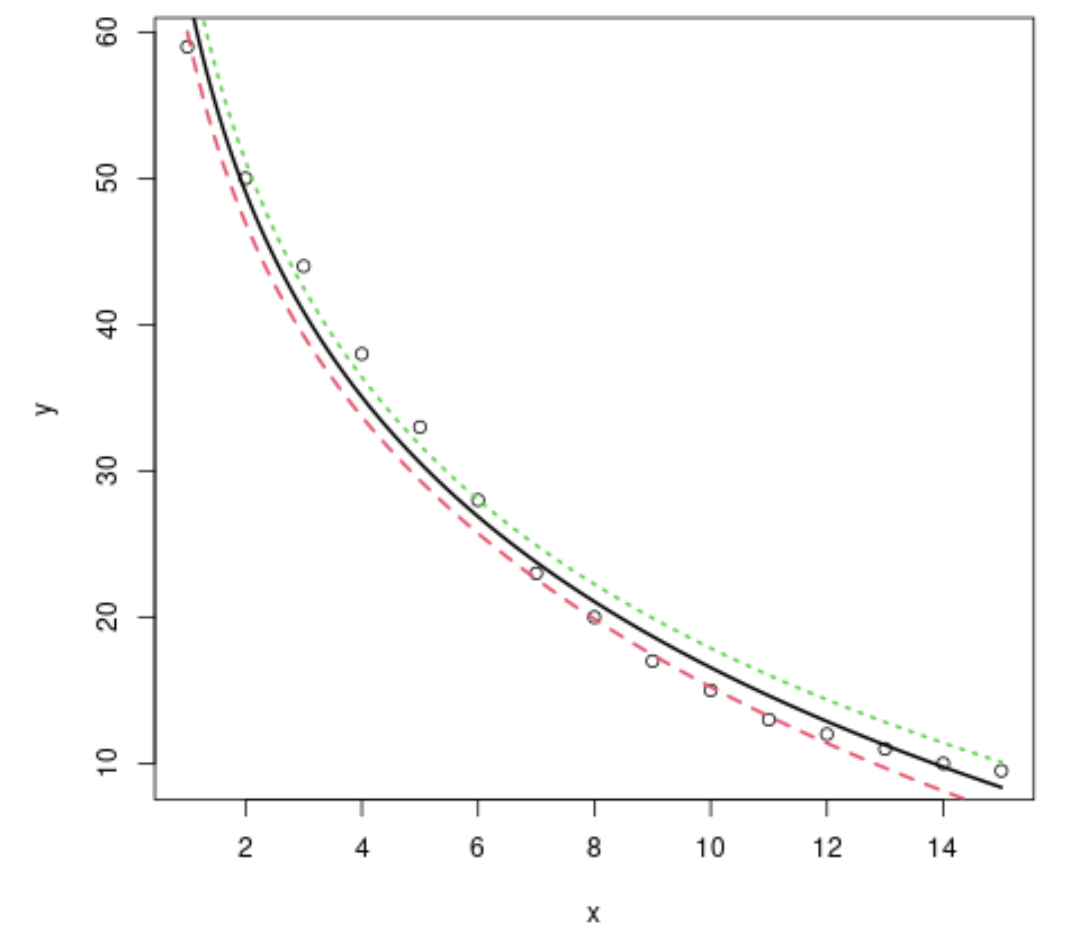
Ми бачимо, що модель логарифмічної регресії добре справляється з підгонкою цього конкретного набору даних.

Додаткові ресурси

Як виконати просту лінійну регресію в R
Як виконати множинну лінійну регресію в R
Як виконати квадратичну регресію в R
Як виконати експоненціальну регресію в R
Як виконати поліноміальну регресію в R