Як виконати логістичну регресію в python (крок за кроком)

Логістична регресія – це метод, який ми можемо використати для підгонки моделі регресії, коли змінна відповіді є двійковою.

Логістична регресія використовує метод, відомий як оцінка максимальної правдоподібності, щоб знайти рівняння такої форми:

log[p(X) / ( ₁ -p(X))] = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p

золото:

• X _j : j- ^та прогнозна змінна
• β _j : оцінка коефіцієнта для j ^-ї прогностичної змінної

Формула в правій частині рівняння передбачає логарифмічні шанси того, що змінна відповіді набере значення 1.

Отже, коли ми підбираємо модель логістичної регресії, ми можемо використовувати наступне рівняння для обчислення ймовірності того, що дане спостереження набуває значення 1:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Потім ми використовуємо певний поріг ймовірності, щоб класифікувати спостереження як 1 або 0.

Наприклад, можна сказати, що спостереження з імовірністю, більшою або рівною 0,5, будуть класифіковані як «1», а всі інші спостереження будуть класифіковані як «0».

Цей підручник надає покроковий приклад виконання логістичної регресії в R.

Крок 1. Імпортуйте необхідні пакети

Спочатку ми імпортуємо необхідні пакети для виконання логістичної регресії в Python:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Крок 2. Завантажте дані

Для цього прикладу ми використаємо набір даних за замовчуванням із книги «Вступ до статистичного навчання» . Ми можемо використати такий код, щоб завантажити та відобразити зведення набору даних:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#view first six rows of dataset
data[0:6]

        default student balance income
0 0 0 729.526495 44361.625074
1 0 1 817.180407 12106.134700
2 0 0 1073.549164 31767.138947
3 0 0 529.250605 35704.493935
4 0 0 785.655883 38463.495879
5 0 1 919.588530 7491.558572  

#find total observations in dataset
len( data.index )

10000

Цей набір даних містить таку інформацію про 10 000 осіб:

• за замовчуванням: вказує, чи особа виконала дефолт чи ні.
• студент: вказує, чи є особа студентом чи ні.
• баланс: середній баланс, який має особа.
• дохід: Дохід фізичної особи.

Ми використаємо статус студента, банківський баланс і дохід, щоб побудувати модель логістичної регресії, яка передбачає ймовірність того, що дана особа не виконає зобов’язання.

Крок 3: Створення навчальних і тестових зразків

Далі ми розділимо набір даних на навчальний набір для навчання моделі та тестовий набір для тестування моделі.

 #define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split (X,y,test_size=0.3,random_state=0)

Крок 4: Підберіть модель логістичної регресії

Далі ми використаємо функцію LogisticRegression() , щоб адаптувати модель логістичної регресії до набору даних:

 #instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

#use model to make predictions on test data
y_pred = log_regression. predict (X_test)

Крок 5: Діагностика моделі

Коли ми підібрали регресійну модель, ми можемо проаналізувати продуктивність нашої моделі на тестовому наборі даних.

Спочатку ми створимо матрицю плутанини для моделі:

 cnf_matrix = metrics. confusion_matrix (y_test, y_pred)
cnf_matrix

array([[2886, 1],
       [113,0]])

З матриці плутанини ми можемо побачити, що:

• #Правдиві позитивні прогнози: 2886
• #Правдиві негативні прогнози: 0
• #Хибні позитивні прогнози: 113
• #Хибні негативні прогнози: 1

Ми також можемо отримати модель точності, яка повідомляє нам відсоток прогнозів корекції, зроблених моделлю:

 print(" Accuracy: ", metrics.accuracy_score (y_test, y_pred))l

Accuracy: 0.962

Це говорить нам про те, що модель зробила правильний прогноз щодо того, чи буде особа дефолт у 96,2% випадків.

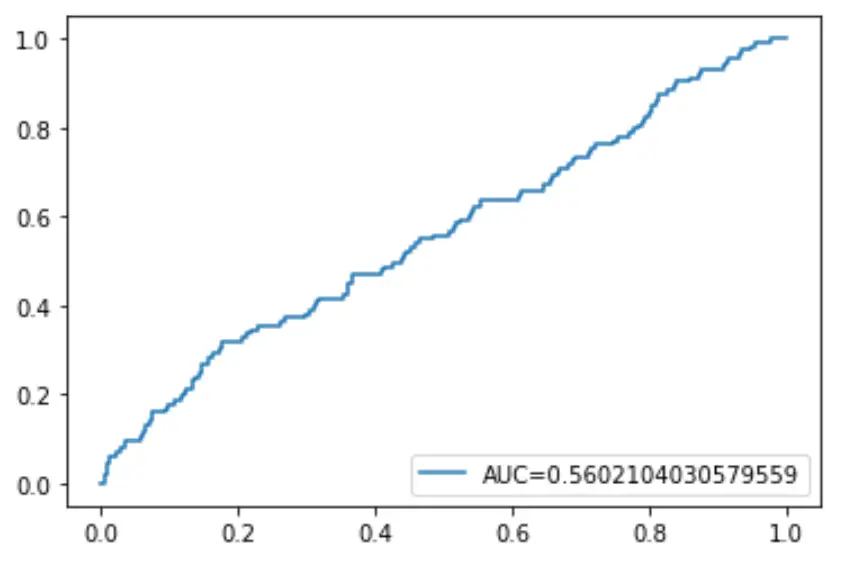
Нарешті, ми можемо побудувати криву робочих характеристик приймача (ROC), яка відображає відсоток істинних позитивних результатів, передбачених моделлю, коли поріг ймовірності прогнозу знижується з 1 до 0.

Чим вище AUC (площа під кривою), тим точніше наша модель здатна передбачити результати:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. legend (loc=4)
plt. show ()