Як виконати логістичну регресію в spss

Логістична регресія – це метод, який ми використовуємо для підгонки моделі регресії , коли змінна відповіді є двійковою.

У цьому посібнику пояснюється, як виконувати логістичну регресію в SPSS.

Приклад: логістична регресія в SPSS

Скористайтеся наведеними нижче кроками, щоб виконати логістичну регресію в SPSS для набору даних, який вказує, чи були задрафтовані студентські баскетболісти в НБА (драфт: 0 = ні, 1 = так) на основі їх середнього балу. очок за гру та їх рівень дивізіону.

Крок 1: Введіть дані.

Спочатку введіть такі дані:

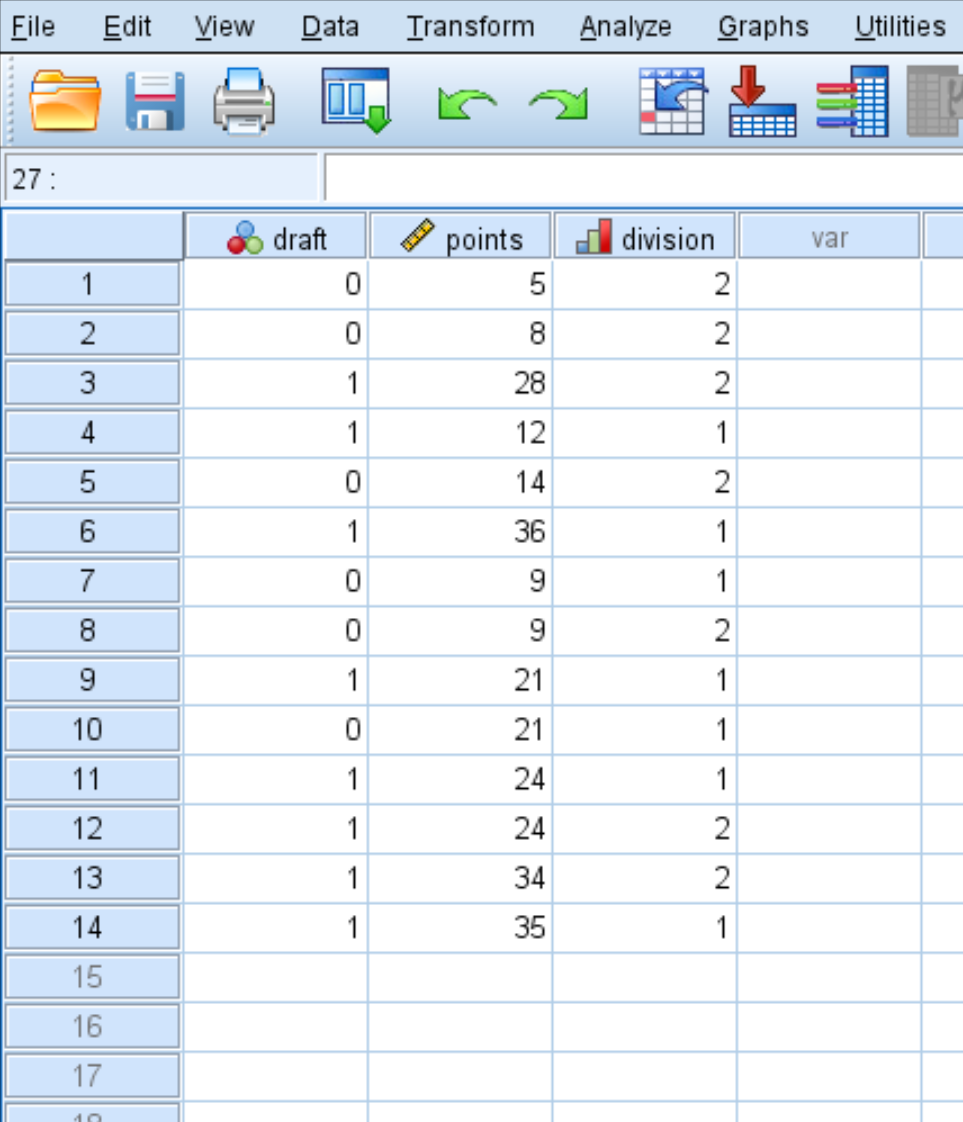
Крок 2: Виконайте логістичну регресію.

Натисніть вкладку «Аналіз» , потім «Регресія» , потім «Двійкова логістична регресія» :

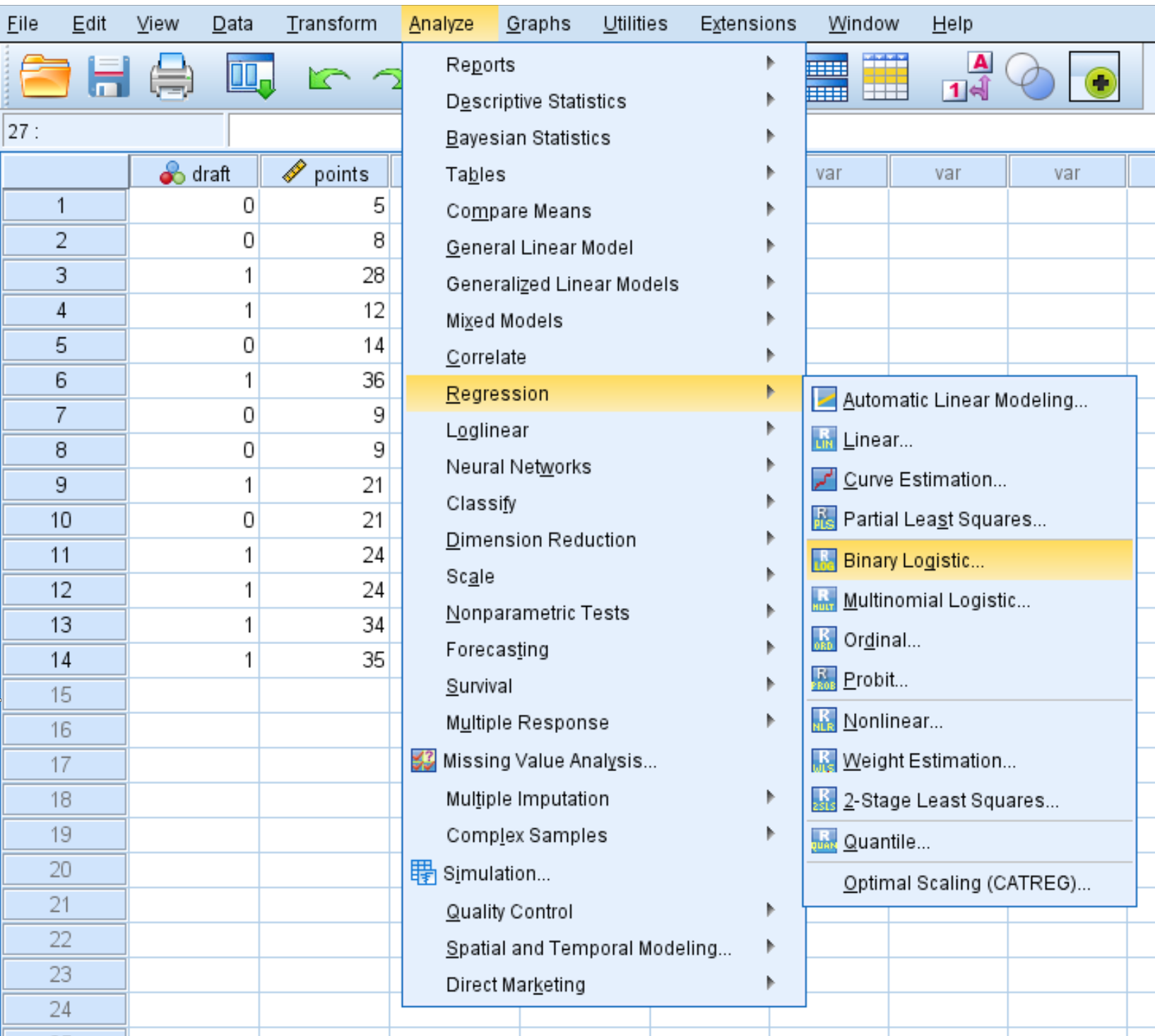
У новому вікні, що з’явиться, перетягніть проект змінної двійкової відповіді в область із позначкою «Залежна». Потім перетягніть двокрапку та ділення змінних предикторів у поле з позначкою Блок 1 з 1. Залиште для методу значення Enter. Потім натисніть OK .

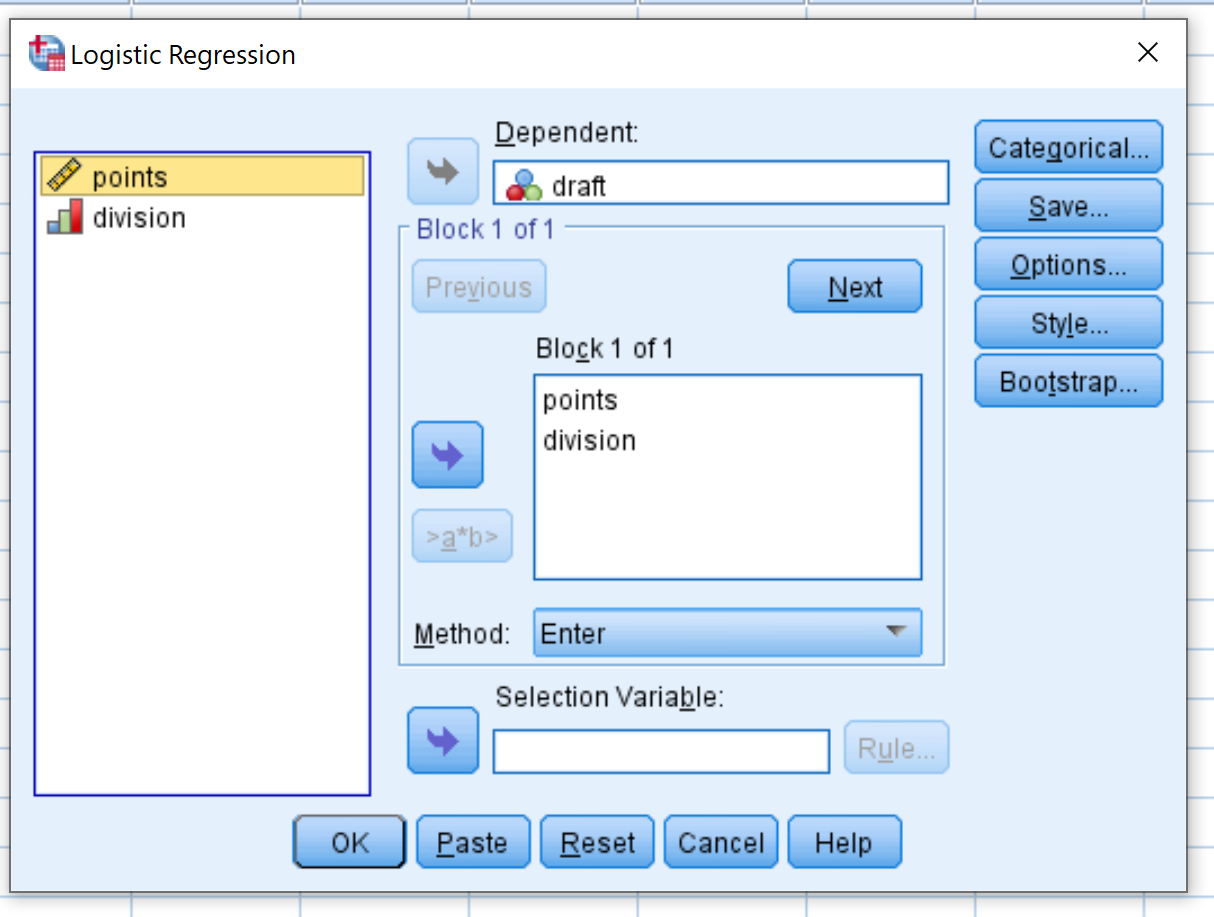
Крок 3. Інтерпретація результату.

Після натискання кнопки OK з’явиться результат логістичної регресії:

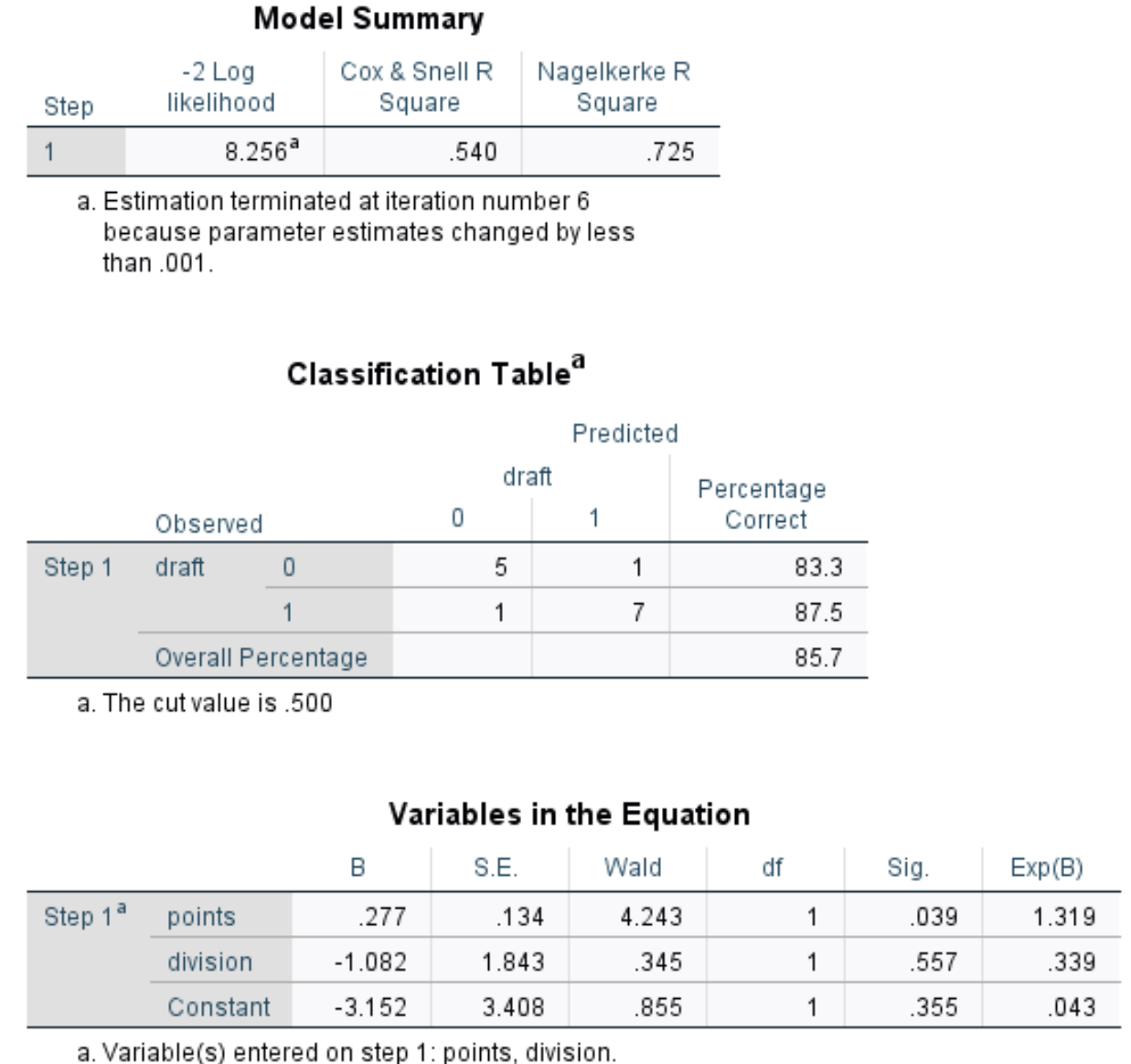
Ось як інтерпретувати результат:

Підсумок моделі: найкориснішим показником у цій таблиці є R-квадрат Нагелькерке, який повідомляє нам про відсоток варіації змінної відповіді , яку можна пояснити змінними-прогнозами. У цьому випадку балами і поділкою можна пояснити 72,5% мінливості тяги.

Таблиця класифікації: найкориснішим показником у цій таблиці є загальний відсоток, який повідомляє нам про відсоток спостережень, які модель змогла правильно класифікувати. У цьому випадку модель логістичної регресії змогла правильно передбачити результат драфту 85,7% гравців.

Змінні в рівнянні: остання таблиця надає нам кілька корисних вимірювань, зокрема:

• Вальда: статистика тесту Вальда для кожної змінної предиктора, яка використовується для визначення того, чи є кожна змінна предиктора статистично значущою чи ні.
• Sig: p-значення, яке відповідає статистиці критерію Вальда для кожної змінної предиктора. Ми бачимо, що p-значення для точок становить 0,039, а p-значення для ділення — 0,557.
• Exp(B): відношення шансів для кожної змінної предиктора. Це вказує нам на зміну шансів гравця, якого забрали, пов’язану зі збільшенням на одну одиницю даної змінної прогнозу. Наприклад, шанси на драфтування гравця Дивізіону 2 становлять лише 0,339 від шансів драфтування гравця Дивізіону 1. Подібним чином кожне додаткове збільшення очок за гру пов’язане зі збільшенням шансів гравця на драфт на 1319.

Потім ми можемо використовувати коефіцієнти (значення в стовпчику B), щоб передбачити ймовірність того, що даний гравець буде обраний, використовуючи таку формулу:

Імовірність = e ^{-3,152 + 0,277 (бали) – 1,082 (поділ)} / (1+e ^{-3,152 + 0,277 (бали) – 1,082 (поділ)} )

Наприклад, ймовірність того, що гравець, який набирає в середньому 20 очок за гру і грає в Дивізіоні 1, буде обраний, можна розрахувати таким чином:

Імовірність = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) = 0,787 .

Оскільки ця ймовірність більша за 0,5, ми б передбачили, що цього гравця буде обрано.

Крок 4. Повідомити про результати.

Нарешті, ми хотіли б повідомити про результати нашої логістичної регресії. Ось приклад того, як це зробити:

Була проведена логістична регресія, щоб визначити, як очки за гру та рівень дивізіону впливають на ймовірність того, що баскетболіст буде обраний. Всього в аналізі було використано 14 гравців.

Модель пояснила 72,5% відхилень у результатах проекту та правильно класифікувала 85,7% випадків.

Шанси на те, що гравець дивізіону 2 буде обраний, становили лише 0,339 шансів гравця дивізіону 1 бути обраним.

Кожне додаткове збільшення очок за гру було пов’язане зі збільшенням шансів гравця на драфт на 1319.