Як виконати лінійну регресію в google таблицях

Лінійна регресія — це метод, який можна використовувати для кількісного визначення зв’язку між однією або декількома пояснювальними змінними та змінною відповіді .

Ми використовуємо просту лінійну регресію, коли є лише одна пояснювальна змінна, і множинну лінійну регресію, коли є дві або більше пояснювальних змінних.

Обидва типи регресій можна виконати за допомогою функції Google Sheets LINEST() , яка використовує такий синтаксис:

LINEST (відомі_дані_y, відомі_дані_x, обчислити_b, докладно)

золото:

• відомі_дані_y: масив значень відповідей
• відомі_дані_x: Таблиця пояснювальних значень
• calculate_b: вказує, чи обчислювати перехоплення. За замовчуванням це TRUE, і ми залишаємо це таким для лінійної регресії.
• verbose: вказує, чи потрібно надавати додаткову статистику регресії, окрім нахилу та перетину. За замовчуванням це FALSE, але ми вкажемо, що це TRUE у наших прикладах.

Наступні приклади показують, як використовувати цю функцію на практиці.

Проста лінійна регресія в Google Таблицях

Припустімо, ми хочемо зрозуміти зв’язок між вивченими годинами та результатами іспиту. підготовка до іспиту та оцінка, отримана на іспиті.

Щоб дослідити цей зв’язок, ми можемо виконати просту лінійну регресію, використовуючи вивчені години як пояснювальну змінну та результати іспитів як змінну відповіді.

На наступному знімку екрана показано, як виконати просту лінійну регресію за допомогою набору даних із 20 студентів із такою формулою, яка використовується в комірці D2:

= РЯДОК ( B2:B21 , A2:A21 , ІСТИНА , ІСТИНА )

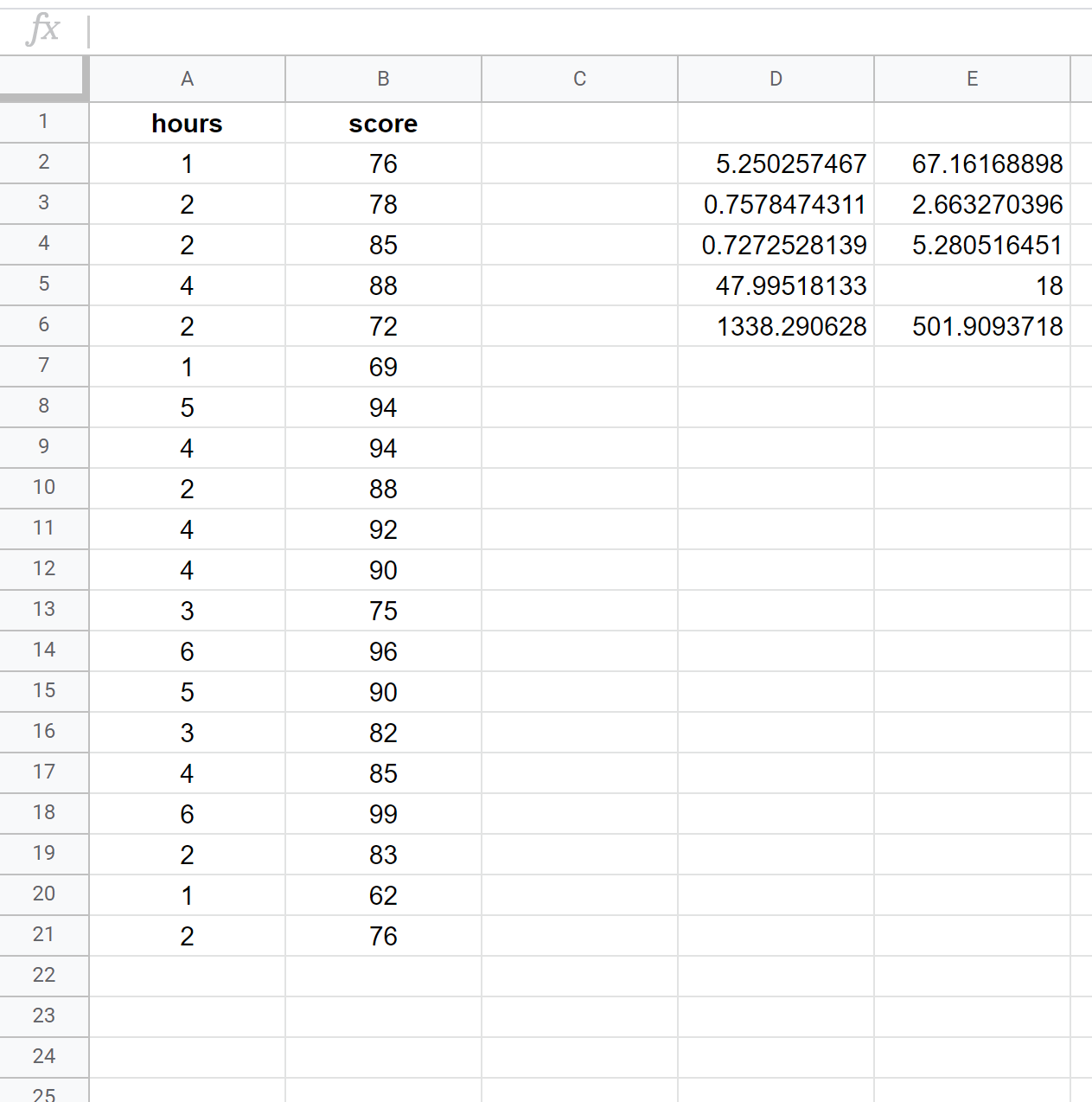
На наступному знімку екрана наведено анотації для результату:

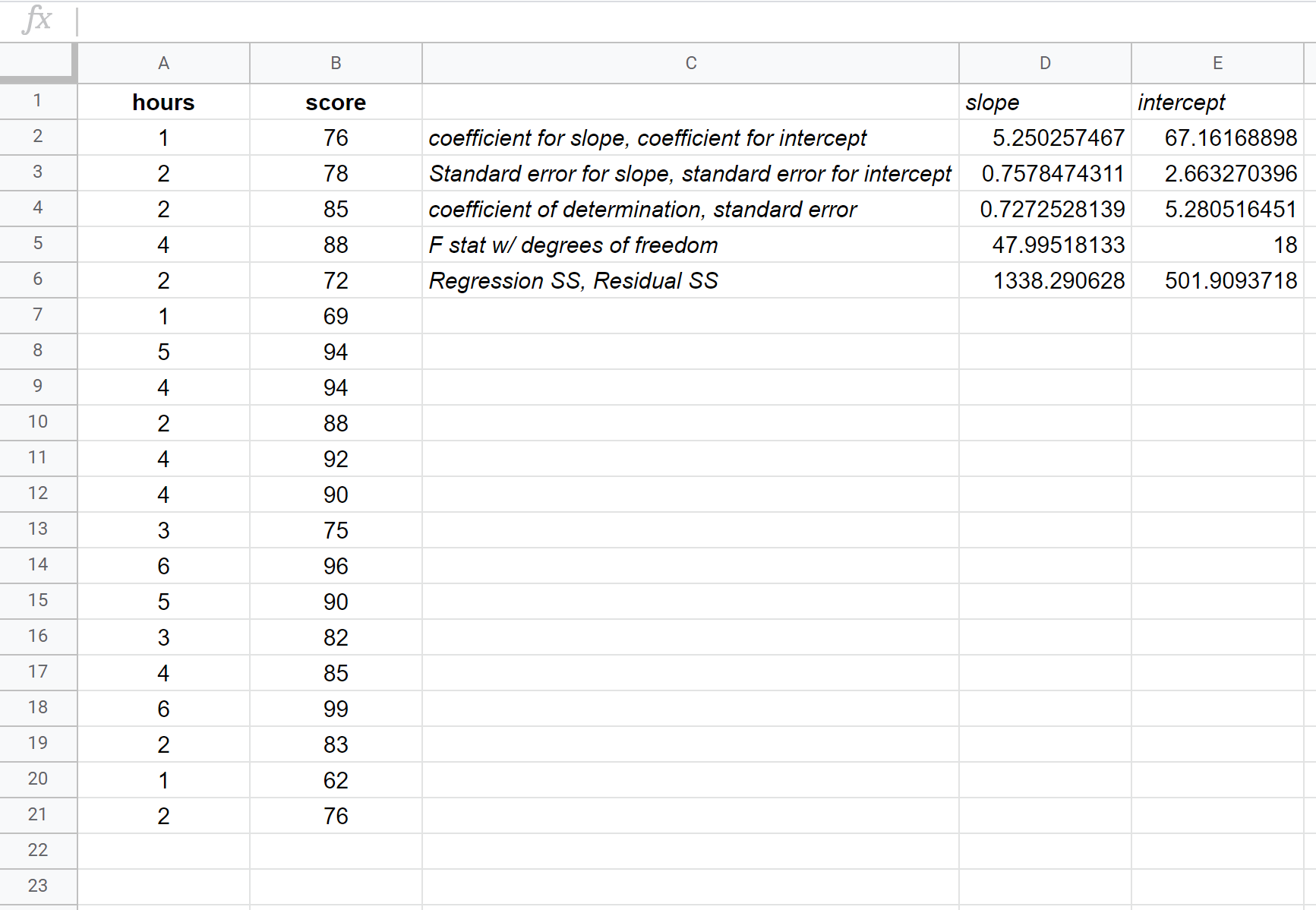
Ось як інтерпретувати найбільш відповідні числа в результаті:

R-квадрат: 0,72725 . Це називається коефіцієнтом детермінації. Це частка дисперсії у змінній відповіді, яку можна пояснити пояснювальною змінною. У цьому прикладі приблизно 72,73% варіації оцінок на іспитах можна пояснити кількістю вивчених годин.

Стандартна похибка: 5,2805 . Це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5,2805 одиниць від лінії регресії.

Коефіцієнти: Коефіцієнти дають нам числа, необхідні для написання розрахункового рівняння регресії. У цьому прикладі розраховане рівняння регресії таке:

Оцінка за іспит = 67,16 + 5,2503*(години)

Ми інтерпретуємо коефіцієнт годин так, що за кожну додаткову вивчену годину оцінка іспиту має зрости в середньому на 5,2503 . Ми інтерпретуємо коефіцієнт перетину так, що очікуваний іспитовий бал для студента, який вивчає нуль годин, становить 67,16 .

Ми можемо використовувати це оцінене рівняння регресії, щоб обчислити очікуваний іспитовий бал для студента на основі кількості годин навчання. Наприклад, студент, який навчається протягом трьох годин, повинен отримати іспитовий бал 82,91 :

Бал іспиту = 67,16 + 5,2503*(3) = 82,91

Множинна лінійна регресія в Google Таблицях

Припустімо, ми хочемо знати, чи впливає кількість годин, витрачених на навчання, і кількість складених підготовчих іспитів на оцінку, яку отримує студент на певному вступному іспиті до коледжу.

Щоб дослідити цей зв’язок, ми можемо виконати множинну лінійну регресію, використовуючи вивчені години та підготовчі іспити як пояснювальні змінні, а результати іспитів – як змінну відповіді.

На наступному знімку екрана показано, як виконати множинну лінійну регресію за допомогою набору даних із 20 студентів із такою формулою, яка використовується в комірці E2:

= ПРАВО ( C2:C21 , A2:B21 , ІСТИНА , ІСТИНА )

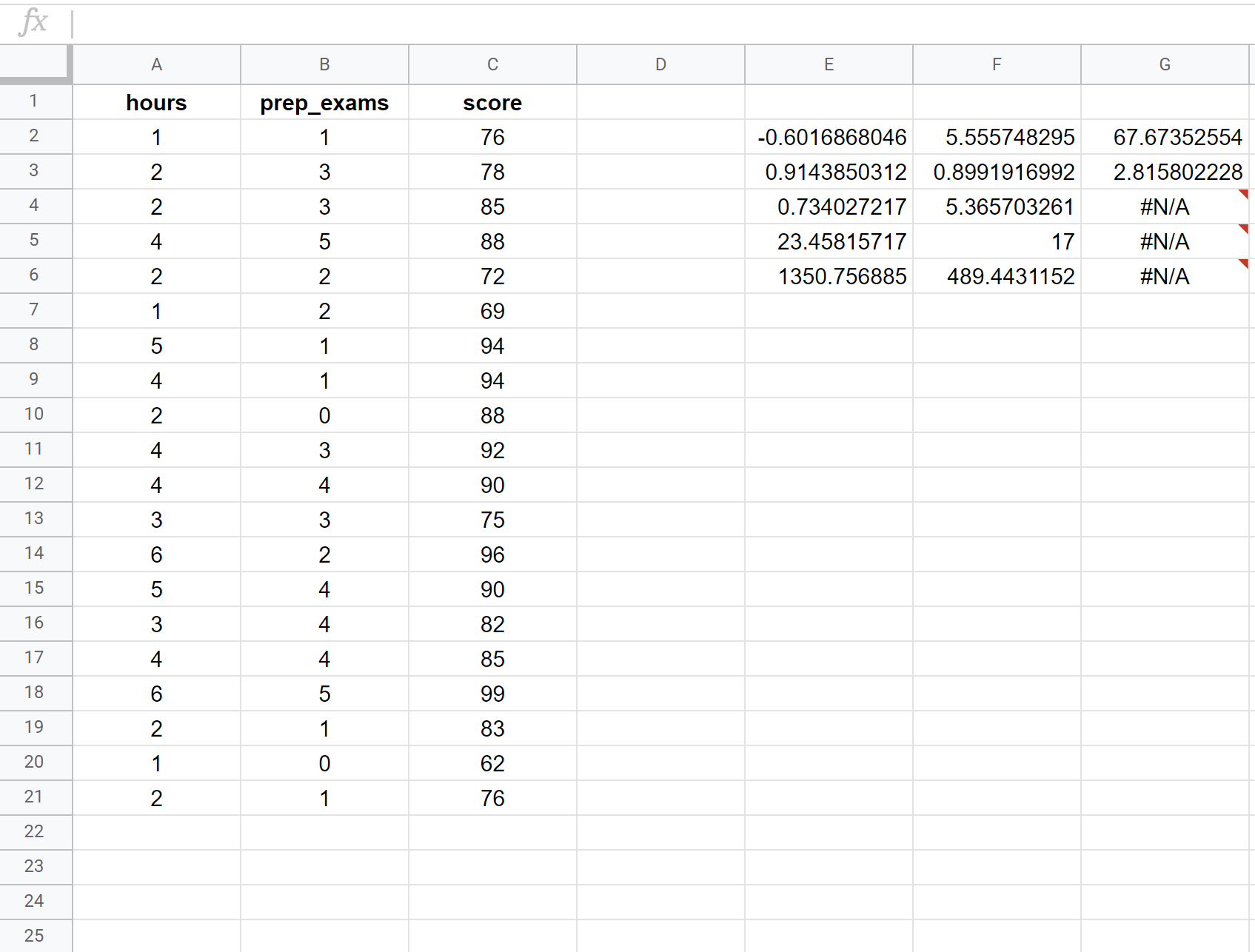
Ось як інтерпретувати найбільш відповідні числа в результаті:

Квадрат R: 0,734 . Це називається коефіцієнтом детермінації. Це частка дисперсії змінної відповіді, яку можна пояснити пояснювальними змінними. У цьому прикладі 73,4% розбіжностей в результатах іспитів пояснюється кількістю вивчених годин і кількістю складених підготовчих іспитів.

Стандартна похибка: 5,3657 . Це середня відстань між спостережуваними значеннями та лінією регресії. У цьому прикладі спостережувані значення відхиляються в середньому на 5,3657 одиниць від лінії регресії.

Розрахункове рівняння регресії: ми можемо використати коефіцієнти з вихідних даних моделі, щоб створити наступне оцінюване рівняння регресії:

Екзамен = 67,67 + 5,56*(годин) – 0,60*(підготовчі іспити)

Ми можемо використати це розраховане рівняння регресії, щоб обчислити очікуваний іспитовий бал для студента на основі кількості годин навчання та кількості практичних іспитів, які він складає. Наприклад, студент, який займається три години і складає підготовчий іспит, повинен отримати оцінку 83,75 :

Бал іспиту = 67,67 + 5,56*(3) – 0,60*(1) = 83,75

Додаткові ресурси

У наведених нижче посібниках пояснюється, як виконувати інші типові завдання в Google Таблицях.

Як виконати поліноміальну регресію в Google Таблицях
Як створити залишковий графік у Google Таблицях