Лінія регресії

за Редакція 2 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке лінія регресії в статистиці. Отже, ви знайдете, як обчислити лінію регресії між двома змінними, розв’язану вправу та, крім того, онлайн-калькулятор для обчислення лінії регресії для будь-якої вибірки даних.

Що таке лінія регресії?

У статистиці лінія регресії — це лінія, отримана з простої моделі лінійної регресії . Точніше, лінія регресії – це лінія, яка найкраще відповідає діаграмі розсіювання і, отже, найкраще описує набір статистичних даних.

Таким чином, рівняння лінії регресії математично пов’язує незалежну змінну X і залежну змінну Y набору даних. Хоча лінія регресії, як правило, не здатна точно визначити значення кожного спостереження, вона може забезпечити наближення його значення.

Як ви бачите на попередньому графіку, лінія регресії допомагає нам побачити тенденцію набору даних і тип зв’язку між незалежною змінною та залежною змінною. Нижче ми розглянемо застосування лінії регресії.

Формула лінії регресії

Тепер, коли ми знаємо визначення лінії регресії, давайте подивимося, як обчислити рівняння лінії моделі лінійної регресії.

Як і будь-яка лінія, рівняння лінії регресії складається з константи (b ₀ ) і нахилу (b ₁ ):

$y=b_0+b_1x$

Таким чином, формули для розрахунку коефіцієнтів лінії лінійної регресії виглядають наступним чином:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

золото:

$b_0$

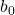
є константою лінії регресії.
$b_1$

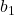
– нахил лінії регресії.
$x_i$

є значенням незалежної змінної X даних i.
$y_i$

є значенням залежної змінної Y даних i.
$\overline{x}$

є середнім значенням незалежної змінної
$\overline{y}$

є середнім значенням залежної змінної Y.

👉 Ви можете використовувати калькулятор нижче, щоб обчислити лінію регресії для будь-якого набору даних.

Конкретний приклад лінії регресії

Щоб глибше вивчити концепцію лінії регресії, нижче наведено робочий приклад того, як створити лінію регресії.

Після іспиту зі статистики п’ятьох студентів запитали, скільки годин навчання вони витратили на іспит, дані наведені в таблиці нижче. Обчисліть лінію регресії на основі зібраних статистичних даних, щоб лінійно зв’язати години навчання з отриманою оцінкою. Далі визначте, яку оцінку отримає учень, який навчався 8 годин.

Щоб знайти лінію регресії для вибіркових даних, нам потрібно визначити коефіцієнти b ₀ і b ₁ рівняння, і для цього нам потрібно використати формули, наведені в розділі вище.

Однак, щоб застосувати формули для лінії лінійної регресії, ми повинні спочатку обчислити середнє значення незалежної змінної та середнє значення залежної змінної:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Тепер, коли ми знаємо середні значення змінних, ми обчислюємо коефіцієнт b ₁ моделі за допомогою відповідної формули:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Нарешті, ми розраховуємо коефіцієнт b ₀ моделі за її відповідною формулою:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Коротше кажучи, рівняння лінії лінійної регресії задачі виглядає наступним чином:

$y=2,0294+0,4412x$

Нижче ви можете побачити графічне представлення вибіркових даних, а також пряму лінію моделі простої лінійної регресії:

Коли ми розрахували лінію регресії, щоб передбачити оцінку, яку отримає студент, який навчався 8 годин, просто підставте це значення в рівняння отриманої лінії регресії:

$y=2,0294+0,4412\cdot 8=5,56$

Таким чином, відповідно до проведеної лінійної регресійної моделі, якщо студент навчався вісім годин, він отримає на іспиті 5,56.

Для чого використовується лінія регресії?

В основному лінія регресії має два застосування: лінія регресії використовується для визначення типу зв’язку між двома змінними, а з іншого боку, лінія регресії також дозволяє зробити прогноз щодо значення нового спостереження.

Нахил лінії регресії говорить нам про кореляцію між незалежною змінною та залежною змінною. Якщо нахил додатний, це означає, що залежна змінна прямо пропорційна незалежній змінній, а якщо нахил від’ємний, це означає, що змінні обернено пропорційні. Нарешті, якщо коефіцієнт нахилу дуже близький до нуля, це означає, що кореляція між двома змінними дуже слабка.

Крім того, якщо відомо рівняння лінії регресії, значення залежної змінної можна передбачити для нового значення незалежної змінної, як ми робили у прикладі вище. Таким чином, чим краще адаптована лінія регресії, тим кращі передбачення вона дасть.

Калькулятор лінії регресії

Введіть зразок даних у наступний калькулятор, щоб обчислити лінію регресії між двома змінними. Потрібно розділити пари даних так, щоб у першому полі були лише значення незалежної змінної X, а в другому – лише значення залежної змінної Y.

Дані повинні бути розділені пробілом і введені крапкою як десятковим роздільником.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше