Як створити матрицю діаграми розсіювання в r (2 приклади)

Матриця діаграми розсіювання — це матриця діаграми розсіювання, яка дозволяє зрозуміти попарний зв’язок між різними змінними в наборі даних.

Існує два поширених способи створення матриці діаграми розсіювання в R:

Спосіб 1: Використовуйте Base R

 #create scatterplot matrix (pch=20 means to use a solid circle for points)
plot(df, pch= 20 )

Спосіб 2: використовуйте пакети ggplot2 і GGally

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df)

У наведених нижче прикладах показано, як використовувати кожен метод на практиці з таким кадром даних у R:

 #create data frame
df <- data. frame (points=c(99, 90, 86, 88, 95, 99, 101, 104),
                 assists=c(33, 28, 31, 39, 40, 40, 35, 47),
                 rebounds=c(30, 28, 24, 24, 20, 20, 15, 12))

#view first few rows of data frame
head(df)

  points assists rebounds
1 99 33 30
2 90 28 28
3 86 31 24
4 88 39 24
5 95 40 20
6 99 40 20

Приклад 1. Створіть матрицю діаграми розсіювання за основою R

Ми можемо використовувати базову функцію R plot() , щоб створити матрицю діаграми розсіювання для кожної змінної в нашому кадрі даних:

 #create scatterplot matrix
plot(df, pch= 20 , cex= 1.5 , col=' steelblue ')

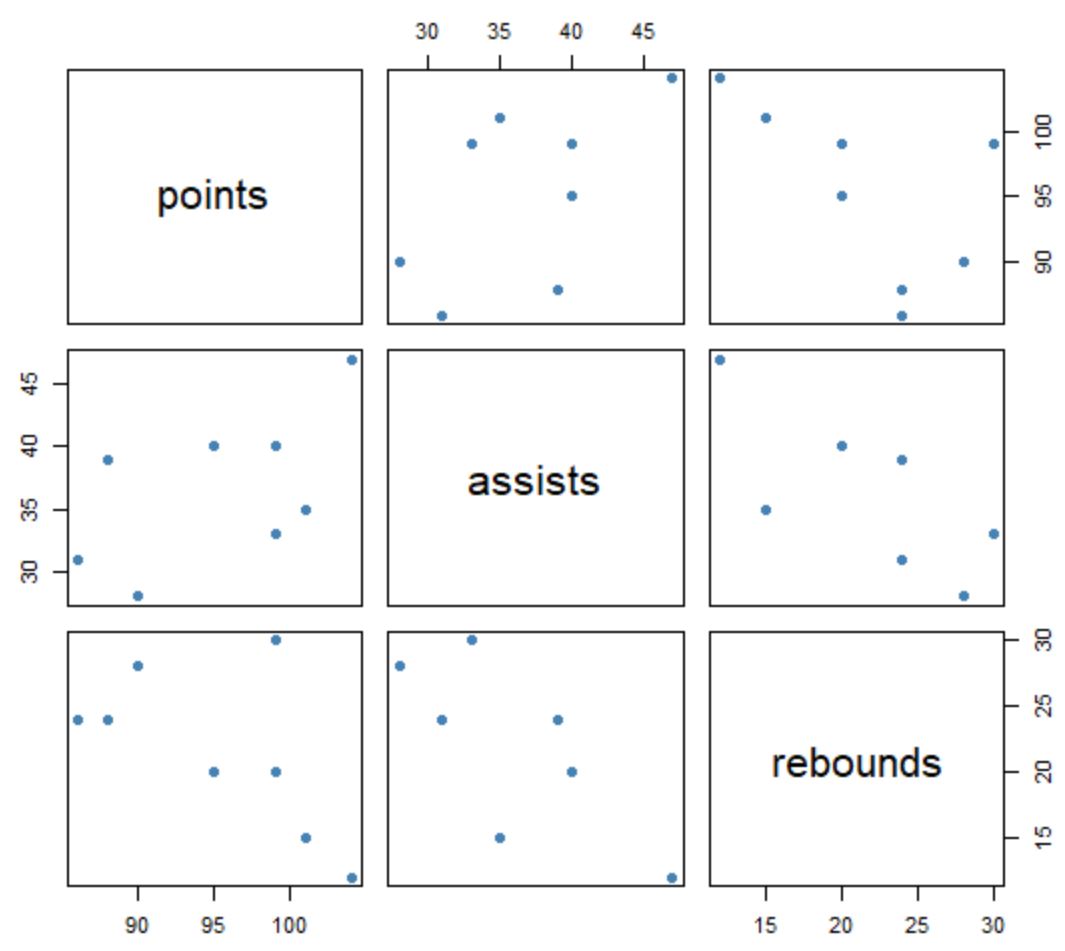
Спосіб інтерпретації матриці такий:

• Назви змінних відображаються вздовж діагональних рамок.
• Усі інші поля відображають діаграму розсіювання зв’язку між кожною попарною комбінацією змінних. Наприклад, поле у верхньому правому куті матриці відображає діаграму розсіювання значень очок і підбирань . Середня ліва область показує діаграму розсіювання значень очок , передач тощо.

Зауважте, що cex керує розміром точок на шляху, а col – кольором точок.

Приклад 2: Створення матриці діаграми розсіювання за допомогою ggplot2 і GGally

Ми також можемо використовувати функцію ggpairs() із пакетів ggplot2 і GGally в R, щоб створити матрицю діаграми розсіювання для кожної змінної в нашому фреймі даних:

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df) 

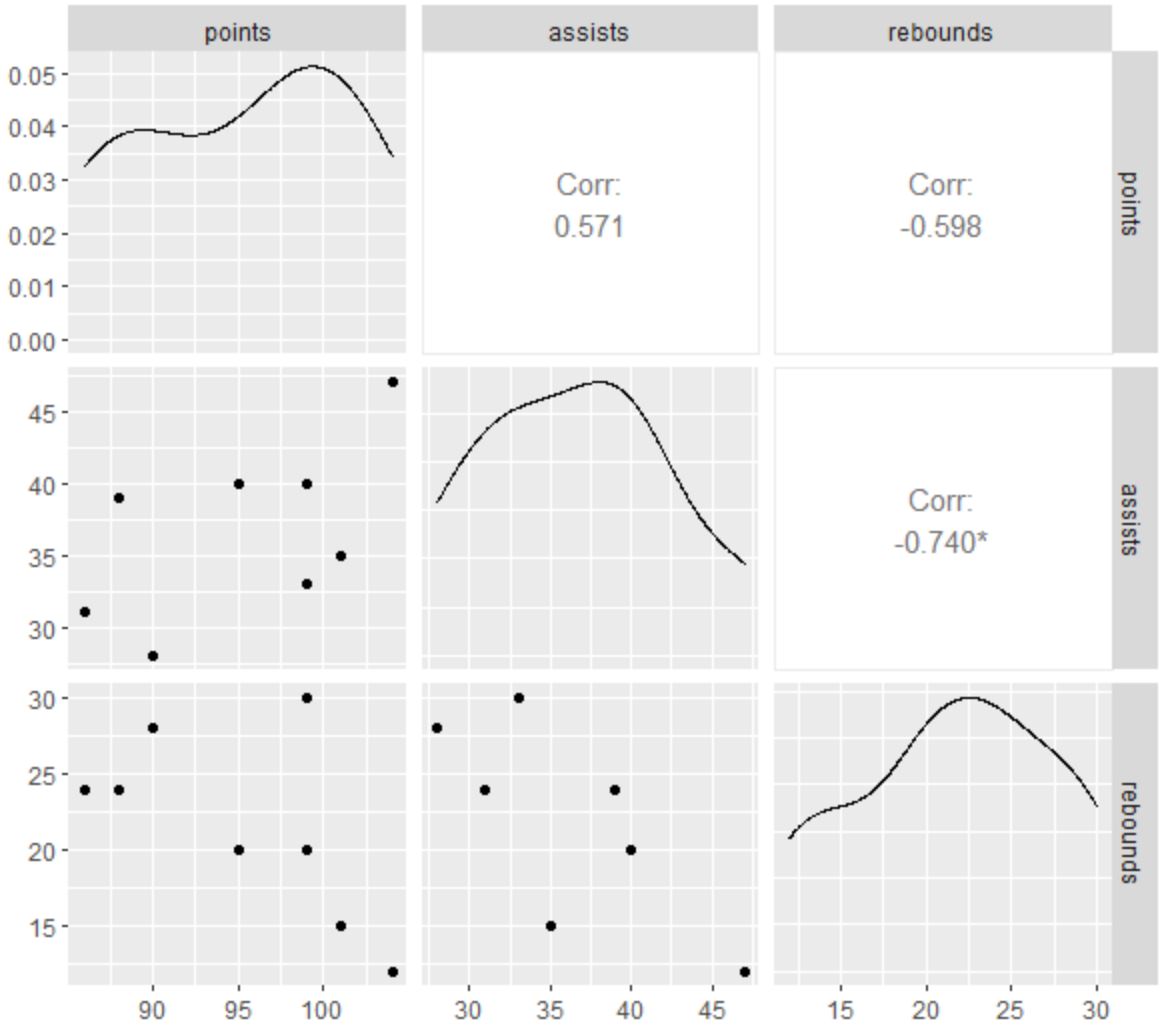
Ця матриця діаграми розсіювання містить ті самі діаграми розсіювання, що й функція R base plot() , але крім того, ми також можемо бачити коефіцієнт кореляції між кожною попарною комбінацією змінних, а також графік щільності для кожної окремої змінної.

Наприклад, ми можемо побачити:

• Коефіцієнт кореляції між передачами та очками становить 0,571 .
• Коефіцієнт кореляції між підбираннями та очками становить -0,598 .
• Коефіцієнт кореляції між підбираннями та передачами становить -0,740 .

Маленька зірочка ( * ) поруч із -0,740 також вказує на те, що кореляція між підбираннями та передачами є статистично значущою.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як створити кореляційну матрицю в R
Як створити хмари точок за групою в R