Як виконати тест шеффе в excel

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

Якщо загальне p-значення таблиці ANOVA нижче певного рівня значущості, тоді ми маємо достатньо доказів, щоб стверджувати, що принаймні одне з групових середніх відрізняється від інших.

Однак це не говорить нам , які групи відрізняються одна від одної. Це просто говорить нам про те, що не всі середні групові показники однакові.

Для того, щоб точно знати, які групи відрізняються одна від одної, нам потрібно виконати пост-хок тест , який може контролювати рівень помилок для сімейства .

Одним із найбільш часто використовуваних пост-тестів є тест Шеффе.

У наступному покроковому прикладі показано, як виконати тест Шеффе в Excel.

Крок 1: Введіть дані

Припустімо, що вчитель хоче знати, чи призводять три різні методи навчання до різних результатів тестів серед учнів. Щоб перевірити це, вона випадковим чином призначає 10 студентів для використання кожної методики навчання та записує їхні результати іспитів.

По-перше, ми введемо оцінки кожного студента на основі використаної методики навчання:

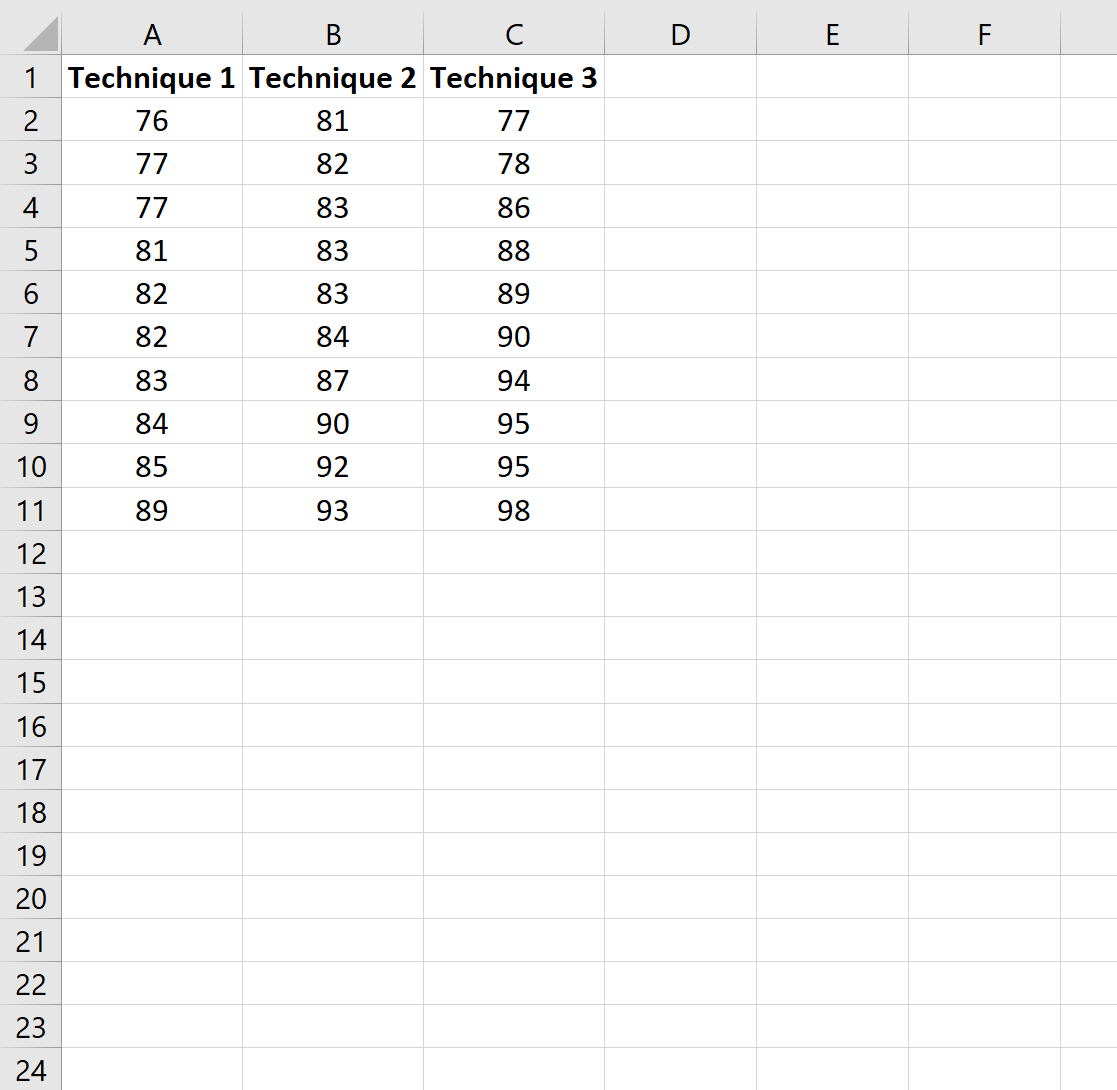
Крок 2: Виконайте односторонній дисперсійний аналіз

Щоб виконати односторонній дисперсійний аналіз, клацніть вкладку «Дані» на верхній стрічці, а потім виберіть параметр «Аналіз даних» у групі «Аналіз» .

Якщо ви не бачите цю опцію, спочатку потрібно завантажити Analysis ToolPak .

У новому вікні, що з’явиться, клацніть Anova: Single Factor, а потім натисніть OK .

У новому вікні, що з’явиться, введіть таку інформацію:

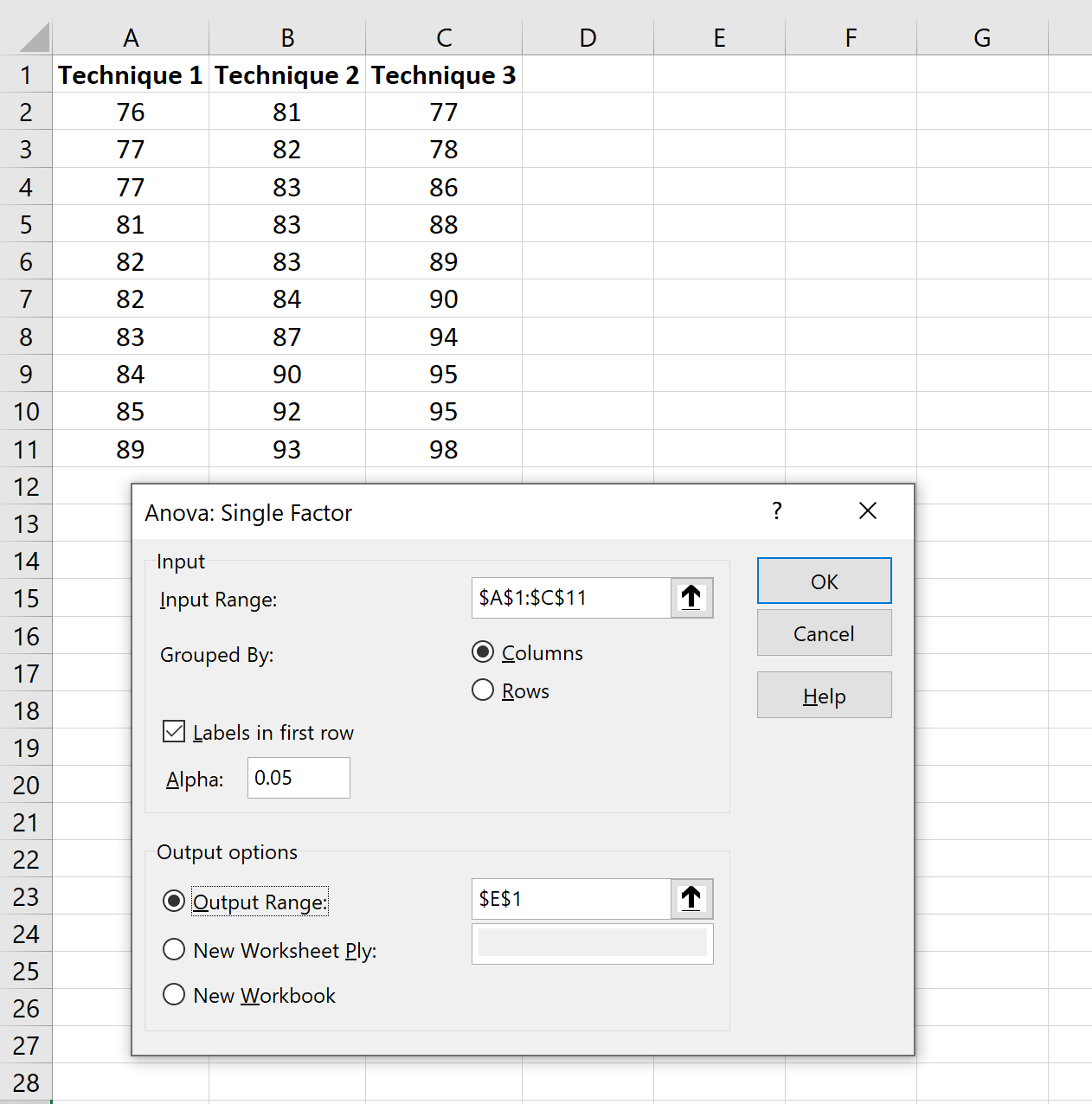
Після натискання кнопки OK з’являться результати одностороннього дисперсійного аналізу:

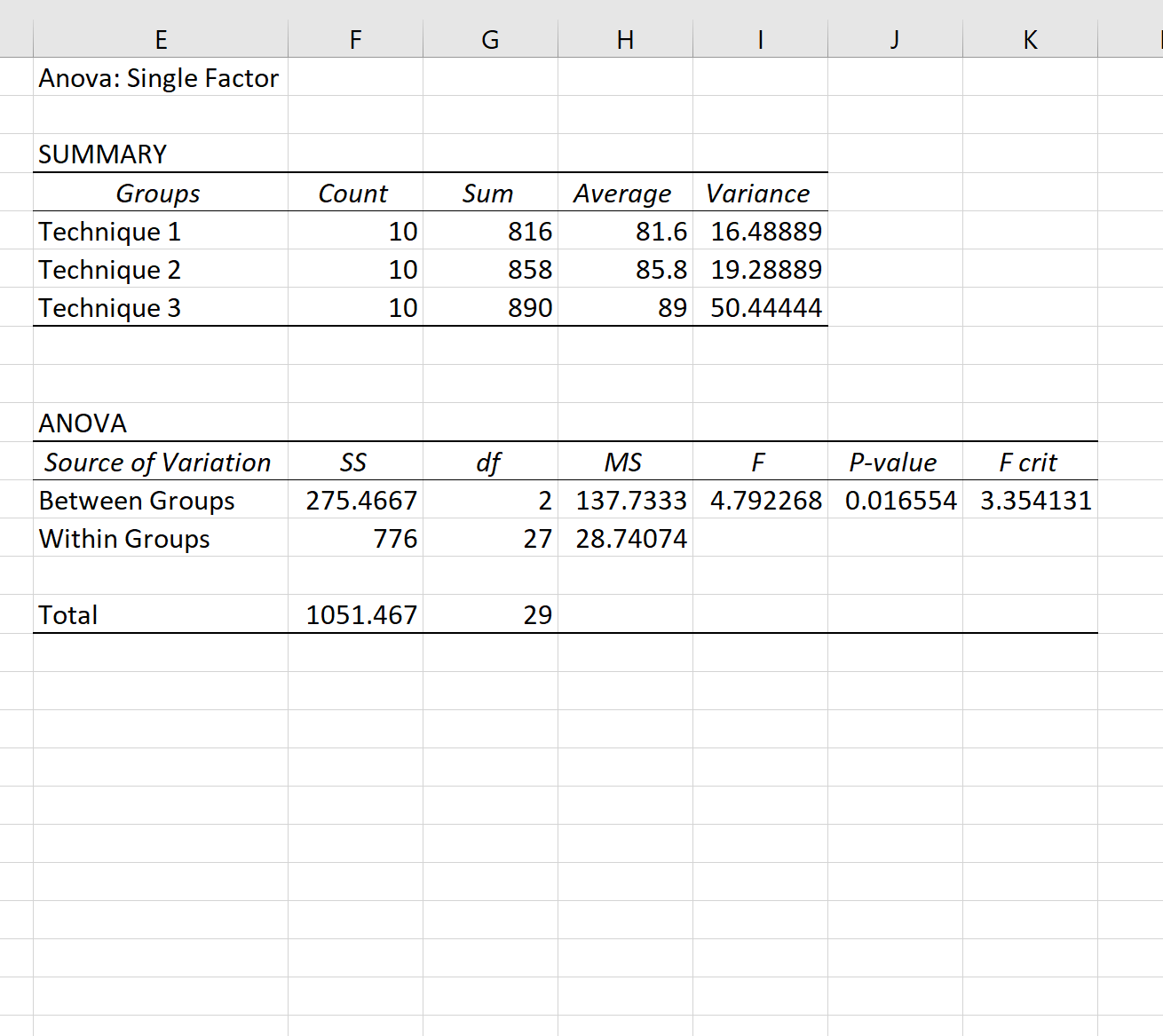
Оскільки загальне значення p ( 0,016554 ) у таблиці ANOVA менше 0,05, це означає, що кожна група не має однакового середнього балу за іспит.

Далі ми виконаємо тест Шеффе, щоб визначити, які групи відрізняються.

Крок 3: Виконайте тест Шеффе

Спочатку нам потрібно обчислити критичне значення Шеффе. Це розраховується таким чином:

Критичне значення Scheffe = F Критичне значення * 2

У нашому прикладі критичне значення Шеффе становить 3,354131 * 2 = 6,708 .

Тоді ми можемо обчислити статистику F для кожного попарного порівняння, яка обчислюється наступним чином:

F-статистика: ( x ₁ – x ₂ ) ² / (MS _в (1/n ₁ + 1/n ₂ ))

Наприклад, ми можемо використовувати наступні формули для розрахунку F-статистики для попарної різниці між кожною технікою:

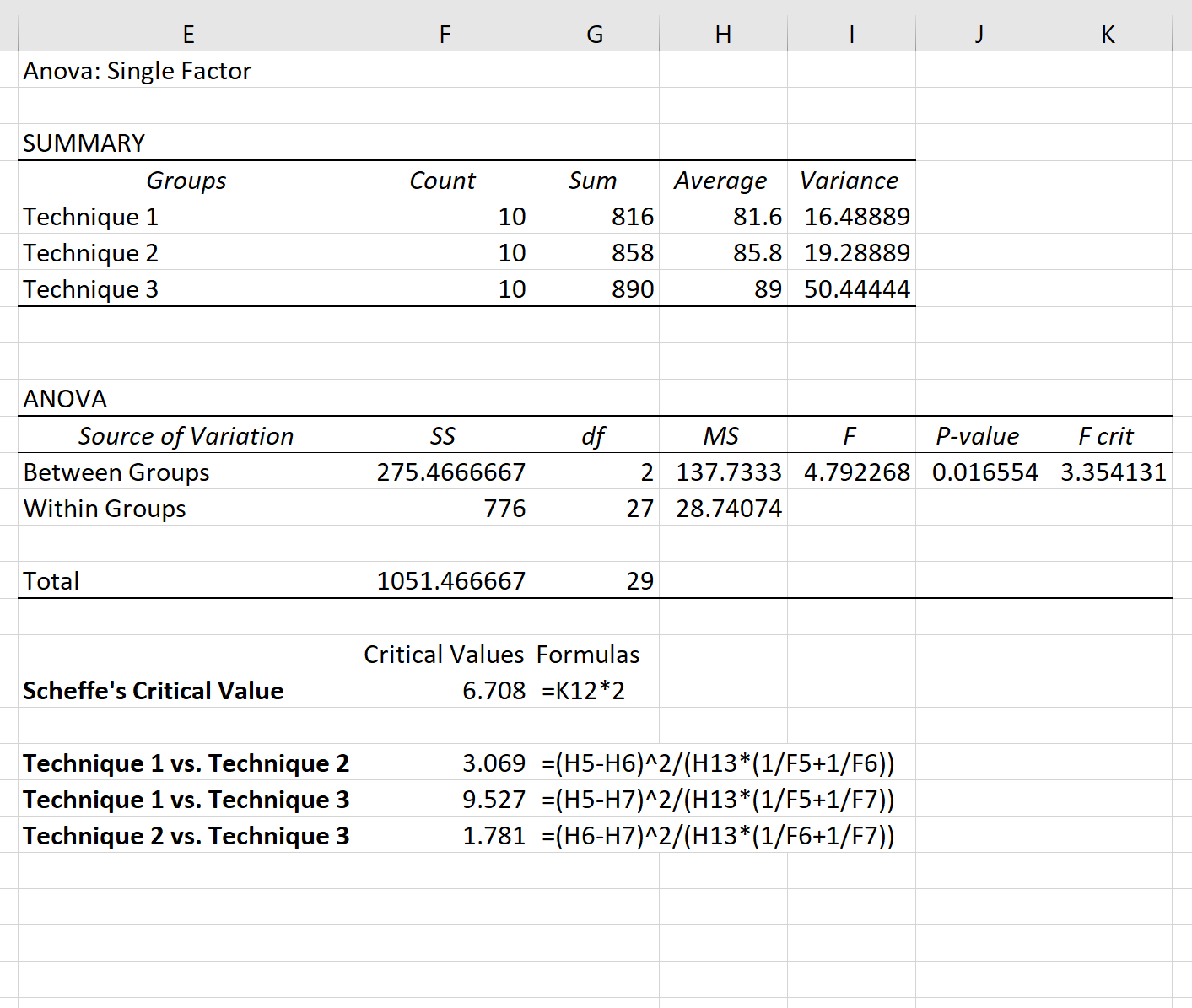
Єдина F-статистика, яка перевищує критичне значення Шеффе, це порівняння між технікою 1 і технікою 3.

Таким чином, єдиними двома статистично суттєво різними групами є техніка 1 і техніка 3.

Додаткові ресурси

Як виконати односторонній дисперсійний аналіз в Excel
Як виконати двосторонній дисперсійний аналіз у Excel
Як виконати пост-тест Тьюкі-Крамера в Excel