Як використовувати метод elbow у python для пошуку оптимальних кластерів

Один із найпоширеніших алгоритмів кластеризації в машинному навчанні відомий як кластеризація k-середніх .

Кластеризація K-означає – це техніка, за якої ми поміщаємо кожне спостереження з набору даних в один із K кластерів.

Кінцева мета полягає в тому, щоб мати K кластерів, у яких спостереження в кожному кластері досить подібні одне до одного, тоді як спостереження в різних кластерах досить відрізняються одне від одного.

Під час кластеризації k-середніх першим кроком є вибір значення для K – кількості кластерів, у які ми хочемо розмістити спостереження.

Один із найпоширеніших способів вибору значення для K відомий як метод ліктя , який передбачає створення графіка з кількістю кластерів на осі абсцис і загальною сумою квадратів на осі у, а потім визначення де в сюжеті з’являється «коліно» або поворот.

Точка на осі X, де виникає «коліно», вказує нам оптимальну кількість кластерів для використання в алгоритмі кластеризації k-середніх.

У наступному прикладі показано, як використовувати метод ліктя в Python.

Крок 1. Імпортуйте необхідні модулі

Спочатку ми імпортуємо всі модулі, які нам знадобляться для кластеризації k-середніх:

 import pandas as pd
import numpy as np
import matplotlib. pyplot as plt
from sklearn. cluster import KMeans
from sklearn. preprocessing import StandardScaler

Крок 2: Створіть DataFrame

Далі ми створимо DataFrame, що містить три змінні для 20 різних баскетболістів:

 #createDataFrame
df = pd. DataFrame ({' points ': [18, np.nan, 19, 14, 14, 11, 20, 28, 30, 31,
                              35, 33, 29, 25, 25, 27, 29, 30, 19, 23],
                   ' assists ': [3, 3, 4, 5, 4, 7, 8, 7, 6, 9, 12, 14,
                               np.nan, 9, 4, 3, 4, 12, 15, 11],
                   ' rebounds ': [15, 14, 14, 10, 8, 14, 13, 9, 5, 4,
                                11, 6, 5, 5, 3, 8, 12, 7, 6, 5]})

#drop rows with NA values in any columns
df = df. dropna ()

#create scaled DataFrame where each variable has mean of 0 and standard dev of 1
scaled_df = StandardScaler(). fit_transform (df)

Крок 3. Використовуйте метод ліктя, щоб знайти оптимальну кількість кластерів

Припустімо, ми хочемо використати кластеризацію k-середніх, щоб згрупувати подібних учасників разом на основі цих трьох показників.

Щоб виконати кластеризацію k-means у Python, ми можемо використати функцію KMeans із модуля sklearn .

Найважливішим аргументом цієї функції є n_clusters , який визначає, у скільки кластерів слід помістити спостереження.

Щоб визначити оптимальну кількість кластерів, ми створимо графік, який відображає кількість кластерів, а також SSE (суму квадратів помилок) моделі.

Потім ми шукатимемо «коліно», де сума квадратів починає «згинатися» або стабілізуватися. Ця точка представляє оптимальну кількість кластерів.

Наступний код показує, як створити цей тип діаграми, яка відображає кількість кластерів на осі X і SSE на осі Y:

 #initialize kmeans parameters
kmeans_kwargs = {
" init ": " random ",
" n_init ": 10,
" random_state ": 1,
}

#create list to hold SSE values for each k
sse = []
for k in range(1, 11):
    kmeans = KMeans(n_clusters=k, ** kmeans_kwargs)
    kmeans. fit (scaled_df)
    sse. append (kmeans.inertia_)

#visualize results
plt. plot (range(1, 11), sse)
plt. xticks (range(1, 11))
plt. xlabel (" Number of Clusters ")
plt. ylabel (“ SSE ”)
plt. show () 

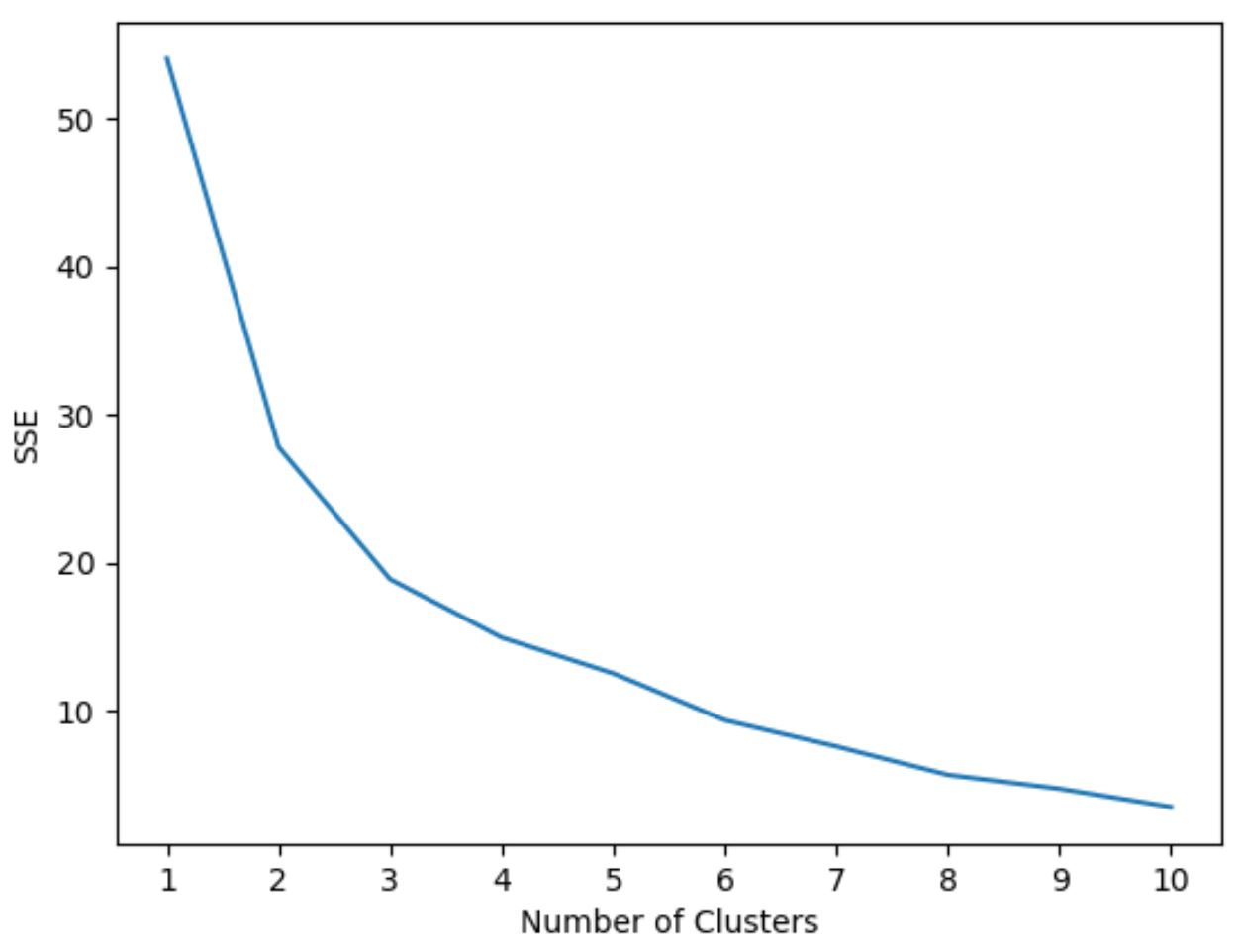
На цьому графіку видно, що є згин або «коліно» при k = 3 кластерах .

Отже, ми будемо використовувати 3 кластери під час адаптації нашої моделі кластеризації k-середніх на наступному кроці.

Крок 4: Виконайте кластеризацію K-середніх із оптимальним K

У наведеному нижче коді показано, як виконати кластеризацію k-середніх для набору даних, використовуючи оптимальне значення для k , рівне 3:

 #instantiate the k-means class, using optimal number of clusters
kmeans = KMeans(init=" random ", n_clusters= 3 , n_init= 10 , random_state= 1 )

#fit k-means algorithm to data
kmeans. fit (scaled_df)

#view cluster assignments for each observation
kmeans. labels_

array([1, 1, 1, 1, 1, 1, 2, 2, 0, 0, 0, 0, 2, 2, 2, 0, 0, 0]) 

Отримана таблиця показує призначення кластерів для кожного спостереження в DataFrame.

Щоб полегшити інтерпретацію цих результатів, ми можемо додати стовпець до DataFrame, який показує кластерне призначення кожного гравця:

 #append cluster assingments to original DataFrame
df[' cluster '] = kmeans. labels_

#view updated DataFrame
print (df)

points assists rebounds cluster
0 18.0 3.0 15 1
2 19.0 4.0 14 1
3 14.0 5.0 10 1
4 14.0 4.0 8 1
5 11.0 7.0 14 1
6 20.0 8.0 13 1
7 28.0 7.0 9 2
8 30.0 6.0 5 2
9 31.0 9.0 4 0
10 35.0 12.0 11 0
11 33.0 14.0 6 0
13 25.0 9.0 5 0
14 25.0 4.0 3 2
15 27.0 3.0 8 2
16 29.0 4.0 12 2
17 30.0 12.0 7 0
18 19.0 15.0 6 0
19 23.0 11.0 5 0

Стовпець кластера містить номер кластера (0, 1 або 2), до якого було призначено кожного гравця.

Гравці, що належать до одного кластеру, мають приблизно однакові значення для стовпців очок , передач і підбирань .

Примітка : повну документацію щодо функції KMeans sklearn можна знайти тут .

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в Python:

Як виконати лінійну регресію в Python
Як виконати логістичну регресію в Python
Як виконати перехресну перевірку K-Fold у Python