Як використовувати метод найменших квадратів у r

Метод найменших квадратів – це метод, який ми можемо використати, щоб знайти лінію регресії, яка найкраще відповідає даному набору даних.

Щоб застосувати метод найменших квадратів для підгонки лінії регресії в R, ми можемо використати функцію lm() .

Ця функція використовує такий базовий синтаксис:

 model <- lm(response ~ predictor, data=df)

У наступному прикладі показано, як використовувати цю функцію в R.

Приклад: метод найменших квадратів у R

Припустімо, що ми маємо наступний кадр даних у R, який показує кількість вивчених годин і відповідний іспитовий бал для 15 студентів у класі:

 #create data frame
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of data frame
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

Ми можемо використовувати функцію lm() , щоб використати метод найменших квадратів, щоб підігнати лінію регресії до цих даних:

 #use method of least squares to fit regression line
model <- lm(score ~ hours, data=df)

#view regression model summary
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

Зі значень у стовпці «Очікуваний результат» ми можемо записати наступну підігнану лінію регресії:

Оцінка за іспит = 65,334 + 1,982 (години)

Ось як інтерпретувати кожен коефіцієнт у моделі:

• Intercept : для студента, який навчається 0 годин, очікуваний бал іспиту становить 65,334 .
• години : за кожну додаткову вивчену годину очікуваний іспитовий бал збільшується на 1982 .

Ми можемо використовувати це рівняння, щоб оцінити іспитову оцінку, яку отримає студент на основі вивчених годин.

Наприклад, якщо студент навчається 5 годин, за нашими оцінками, його іспитовий бал становитиме 75,244:

Оцінка іспиту = 65,334 + 1,982(5) = 75,244

Нарешті, ми можемо створити діаграму розсіювання вихідних даних з підігнаною лінією регресії, накладеною на графік:

 #create scatter plot of data
plot(df$hours, df$score, pch=16, col=' steelblue ')

#add fitted regression line to scatter plot
abline(model)

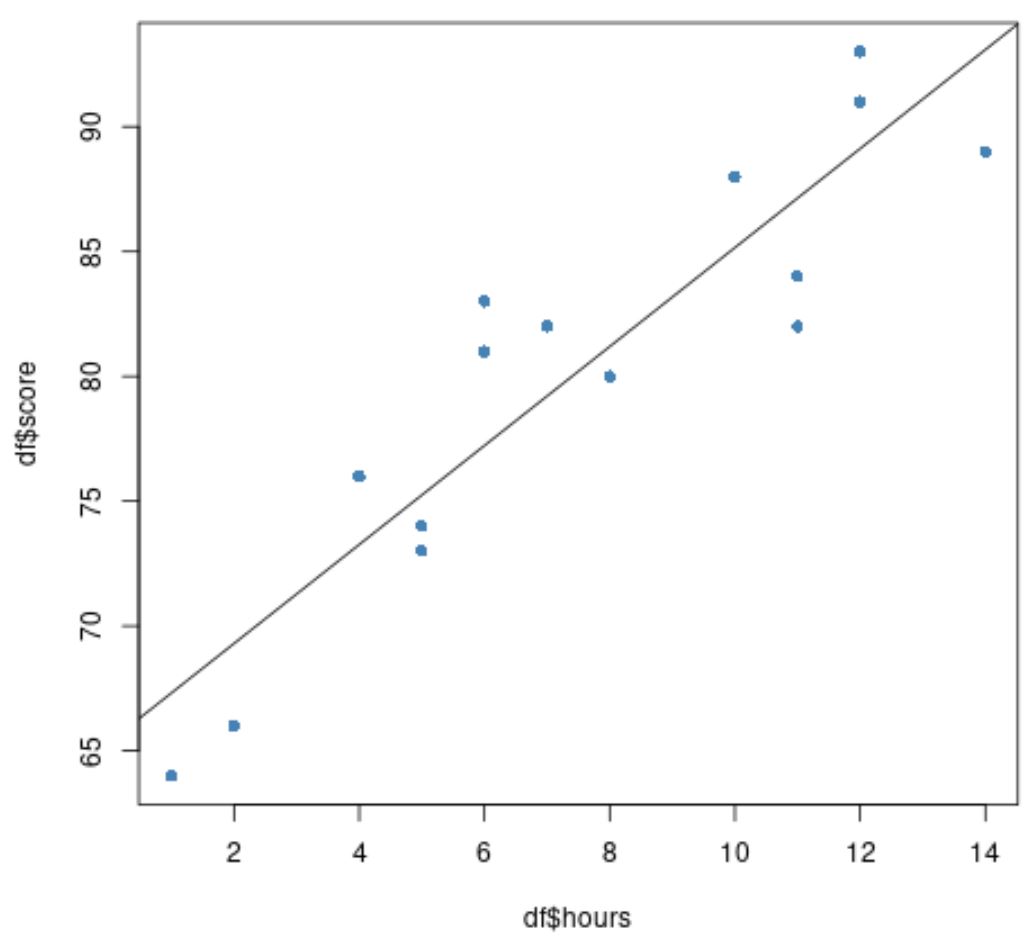
Сині кружечки позначають дані, а чорна лінія – підігнану лінію регресії.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в R:

Як створити ділянку залишків у R
Як перевірити мультиколінеарність у R
Як виконати підгонку кривої в R