Як виконати множинну лінійну регресію в sas

Множинна лінійна регресія – це метод, який ми можемо використати для розуміння зв’язку між двома чи більше змінними предикторами та змінною відповіді .

У цьому посібнику пояснюється, як виконувати множинну лінійну регресію в SAS.

Крок 1: Створіть дані

Припустімо, ми хочемо підібрати модель множинної лінійної регресії, яка використовує кількість годин, витрачених на навчання, і кількість складених практичних іспитів, щоб передбачити оцінку студентів на підсумкових іспитах:

Оцінка за іспит = β ₀ + β ₁ (годин) + β ₂ (підготовчі іспити)

Спочатку ми використаємо наступний код, щоб створити набір даних, що містить цю інформацію для 20 студентів:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Крок 2: Виконайте множинну лінійну регресію

Далі ми використаємо proc reg , щоб підібрати модель множинної лінійної регресії до даних:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

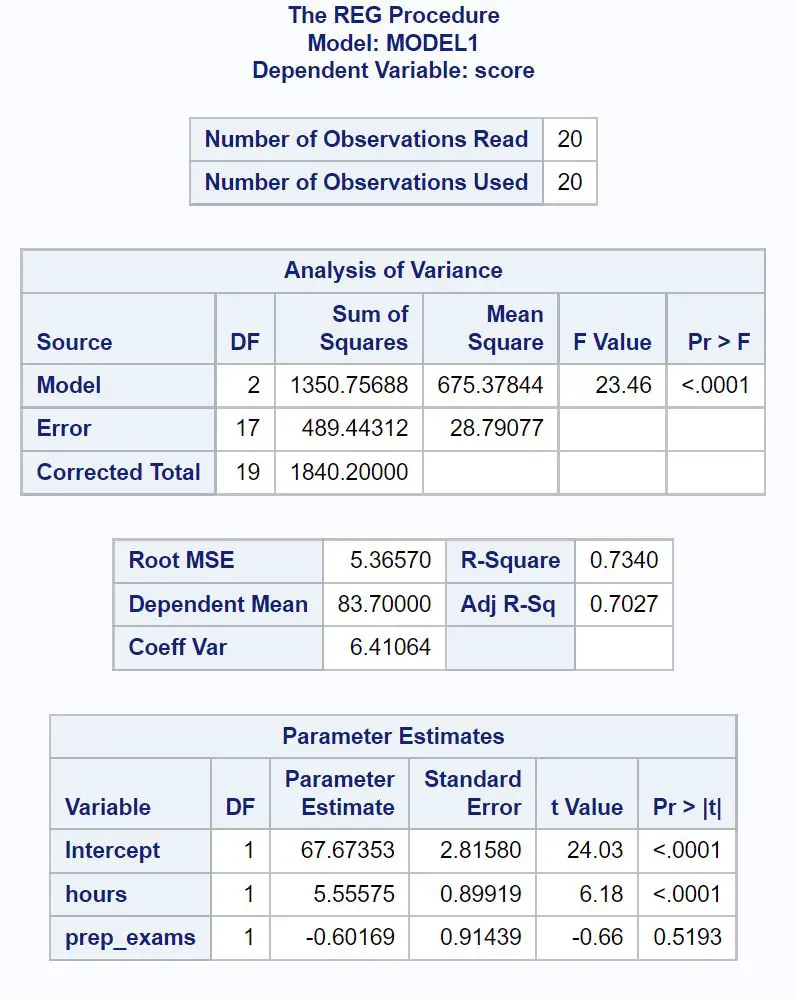
Ось як інтерпретувати найбільш відповідні числа в кожній таблиці:

Таблиця аналізу прогалин:

Загальне F-значення регресійної моделі становить 23,46 , а відповідне значення p <0,0001 .

Оскільки це p-значення менше 0,05, ми робимо висновок, що регресійна модель в цілому є статистично значущою.

Модельний стіл:

Значення R-квадрат показує нам відсоток варіації оцінок іспитів, який можна пояснити кількістю вивчених годин і кількістю складених підготовчих іспитів.

Загалом, чим більше значення R-квадрат регресійної моделі, тим краще прогностичні змінні прогнозують значення змінної відповіді.

У цьому випадку 73,4% розбіжності в іспитових балах можна пояснити кількістю вивчених годин і кількістю складених підготовчих іспитів.

Значення Root MSE також корисно знати. Це являє собою середню відстань між спостережуваними значеннями та лінією регресії.

У цій моделі регресії спостережувані значення відхиляються в середньому на 5,3657 одиниць від лінії регресії.

Таблиця оцінок параметрів:

Ми можемо використовувати оціночні значення параметрів у цій таблиці, щоб написати підігнане рівняння регресії:

Оцінка за іспит = 67,674 + 5,556*(годин) – 0,602*(підготовчі іспити)

Ми можемо використати це рівняння, щоб знайти приблизний бал студента за іспит на основі кількості годин навчання та кількості практичних іспитів, які вони склали.

Наприклад, студент, який навчається 3 години і складає 2 підготовчі іспити, повинен отримати іспитовий бал 83,1 :

Приблизний бал за іспит = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

P-значення для годин (<0,0001) менше 0,05, що означає, що воно має статистично значущий зв’язок із результатом іспиту.

Проте значення p для підготовчих іспитів (0,5193) не менше 0,05, що означає, що воно не має статистично значущого зв’язку з результатом іспиту.

Ми можемо вирішити видалити підготовчі іспити з моделі, оскільки вони не є статистично значущими, і натомість виконати просту лінійну регресію , використовуючи досліджувані години як єдину змінну прогнозу.

Додаткові ресурси

У наступних посібниках пояснюється, як виконувати інші типові завдання в SAS:

Як розрахувати кореляцію в SAS
Як виконати просту лінійну регресію в SAS
Як виконати односторонній дисперсійний аналіз у SAS