Що таке багаточленний тест? (визначення & #038; приклад)

Мультиноміальний тест використовується, щоб визначити, чи відповідає категоріальна змінна гіпотетичному розподілу.

Цей тест використовує такі нульові та альтернативні гіпотези :

H ₀ : категоріальна змінна відповідає гіпотетичному розподілу.

H _A : категоріальна змінна не відповідає гіпотетичному розподілу.

Якщо p-значення тесту нижче певного рівня значущості (наприклад, α = 0,05), тоді ми можемо відхилити нульову гіпотезу та зробити висновок, що змінна не відповідає гіпотетичному розподілу.

Цей тест використовується, коли змінна може отримати k різних результатів. Класичним прикладом багаточленного тесту є те, коли ми хочемо визначити, чи є певні кубики справедливими. Коли ви кидаєте кубик, ймовірність того, що він випаде на кожне число (від 1 до 6), становить 1/6.

Щоб перевірити, чи справедливий кубик, ми можемо кинути його кілька разів і перевірити, чи кількість разів, коли він потрапляє на різні числа, суттєво відрізняється від очікуваного.

У наступних прикладах показано, як виконати мультиноміальний тест за допомогою мови статистичного програмування R.

Приклад 1: Чесні кубики

Припустімо, ми хочемо визначити, чи справедливий кубик. Щоб перевірити це, ми запускаємо його 30 разів і записуємо частоту кожного результату. У наступній таблиці показано результати:

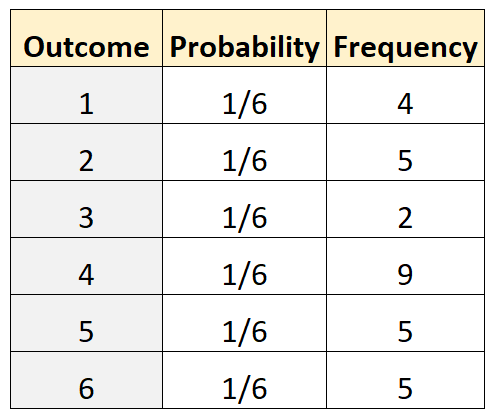
Наступний код у R можна використовувати для виконання багаточленного тесту:

 library (EMT)

#specify probability of each outcome
prob <- c(1/6, 1/6, 1/6, 1/6, 1/6, 1/6)

#specify frequency of each outcome from experiment
actual <- c(4, 5, 2, 9, 5, 5)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    324632 0 0.4306

P-значення тесту становить 0,4306 . Оскільки це p-значення не менше 0,05, ми не відкидаємо нульову гіпотезу. Отже, у нас недостатньо доказів, щоб стверджувати, що кості несправедливі.

Приклад 2: Продаж продукції

Припустімо, що власник магазину припускає, що рівна кількість покупців придбає кожен із чотирьох різних продуктів. Щоб перевірити це, він записує кількість клієнтів, які придбали кожен продукт за певний тиждень. У наступній таблиці показано результати:

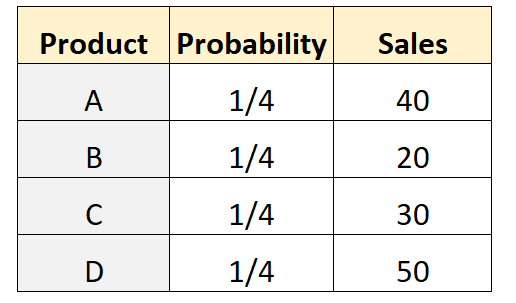
Наступний код у R можна використовувати для виконання багаточленного тесту на цьому наборі даних:

 library (EMT)

#specify probability of each outcome
prob <- c(1/4, 1/4, 1/4, 1/4)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
    477191 0 0.00226

P-значення тесту становить 0,00226 . Оскільки це p-значення менше 0,05, ми відхилимо нульову гіпотезу. Отже, ми маємо достатньо доказів, щоб стверджувати, що продажі не однакові для кожного продукту.

Приклад 3: кульки в мішку

Том стверджує, що ймовірність вибору червоного, зеленого або фіолетового кульки з мішка становить 0,2, 0,5 і 0,3 відповідно. Щоб перевірити це, його друг Майк лізе в сумку і дістає кульку (із замінами) 100 різних разів. У наступній таблиці показано результати:

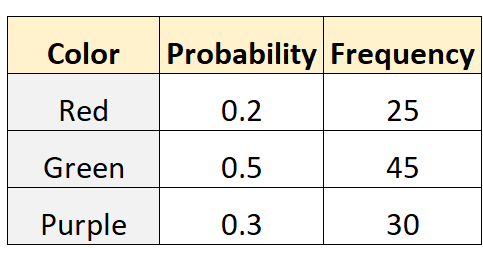
Наступний код у R можна використовувати для виконання багаточленного тесту на цьому наборі даних:

 library (EMT)

#specify probability of each outcome
prob <- c(.2, .5, .3)

#specify frequency of each outcome from experiment
actual <- c(40, 20, 30, 50)

#perform multinomial test
multinomial. test (actual, prob) 

 Exact Multinomial Test, distance measure: p

    Events pObs p.value
      5151 0.0037 0.3999

P-значення тесту становить 0,3999 . Оскільки це p-значення не менше 0,05, ми не зможемо відхилити нульову гіпотезу. Тому ми не маємо достатньо доказів, щоб стверджувати, що розподіл кульок у мішку відрізняється від зазначеного Томом.

Додаткові ресурси

Вступ до мультиноміального розподілу
Калькулятор мультиноміального розподілу