Найменш значуща відмінність фішера: визначення + приклад

Односторонній дисперсійний аналіз використовується, щоб визначити, чи існує статистично значуща різниця між середніми значеннями трьох або більше незалежних груп.

У дисперсійному аналізі використовуються такі припущення :

H ₀ : Середні значення рівні для кожної групи.

H _A : Принаймні один із способів відрізняється від інших.

Якщо p-значення ANOVA нижче певного рівня значущості (наприклад, α = 0,05), ми можемо відхилити нульову гіпотезу та зробити висновок, що принаймні одне з групових середніх відрізняється від інших.

Але щоб точно знати, які групи відрізняються одна від одної, нам потрібно провести ретельний тест.

Зазвичай використовуваним пост-критерієм є критерій найменшої значущої різниці Фішера .

Щоб виконати цей тест, ми спочатку обчислюємо таку тестову статистику:

LSD = t _0,025 , _{DF w} * √ MS _W (1/n ₁ + 1/n ₁ )

золото:

• t _.025 , _DFw : t-критичне значення таблиці розподілу t з α = .025 і DF _w відповідає ступеням свободи в межах груп таблиці ANOVA.
• MS _W : Середні квадрати в межах груп у таблиці ANOVA.
• n ₁ , n ₂ : розміри вибірки кожної групи

Потім ми можемо порівняти середню різницю між кожною групою з цією тестовою статистикою. Якщо абсолютне значення середньої різниці між двома групами перевищує тестову статистику, ми можемо оголосити, що існує статистично значуща різниця між груповими середніми.

У наступному прикладі показано, як на практиці виконати критерій найменшої значущої різниці Фішера.

Приклад: Критерій різниці найменшої значимості Фішера

Припустімо, професор хоче знати, чи призводять три різні методи навчання до різних результатів тестів серед студентів. Щоб перевірити це, вона випадковим чином призначає 10 студентів для використання кожної методики навчання та записує їхні результати іспитів.

У наведеній нижче таблиці наведено результати іспиту кожного студента на основі використаної методики навчання:

Професор виконує односторонній дисперсійний аналіз і отримує такі результати:

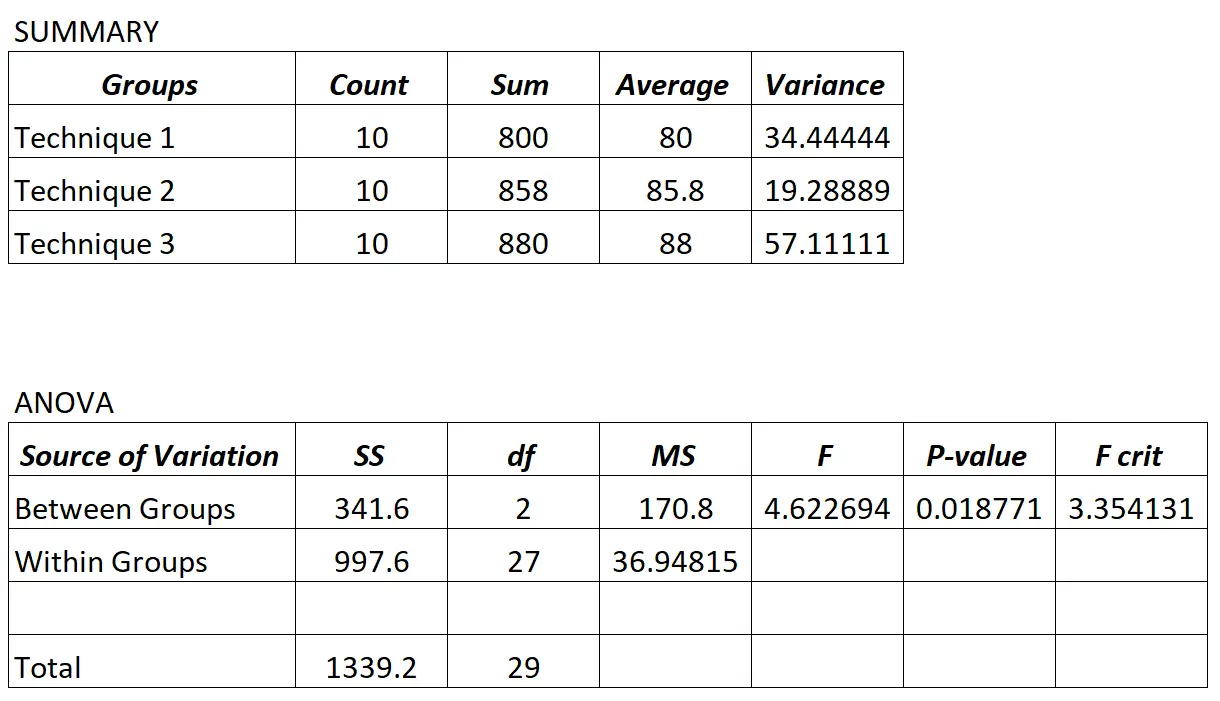
Оскільки p-значення в таблиці ANOVA (0,018771) менше 0,05, ми можемо зробити висновок, що всі середні результати іспиту між трьома групами не однакові.

Отже, ми можемо виконати критерій найменшої значущої різниці Фішера, щоб визначити, які групові середні відрізняються.

Використовуючи значення з результату ANOVA, ми можемо розрахувати статистику критерію Фішера наступним чином:

• LSD = t _0,025 , _DFw * √ MS _W (1/n ₁ + 1/n ₁ )
• LSD = t _0,025 , ₂₇ * √ 36,948 * (1/10 + 1/10)
• LSD = 2,052 * √ 7,3896
• ЛСД = 5,578

Потім ми можемо обчислити абсолютну середню різницю між кожною групою:

• Техніка 1 проти Техніки 2: |80 – 85,8| = 5,8
• Техніка 1 проти Техніки 3: |80 – 88| = 8
• Техніка 2 проти Техніки 3: |85,8 – 88| = 2,2

Абсолютні середні відмінності між технікою 1 і технікою 2, а також між технікою 1 і технікою 3 є більшими, ніж статистика тесту Фішера. Таким чином, ми можемо зробити висновок, що ці методи призводять до статистично суттєво відмінних середніх балів на іспитах.

Ми також можемо зробити висновок, що немає істотної різниці в середніх іспитових балах між технікою 2 і технікою 3.