Часткові найменші квадрати в python (крок за кроком)

Одна з найпоширеніших проблем, з якою ви зіткнетеся під час машинного навчання, — мультиколінеарність . Це відбувається, коли дві або більше змінних предиктора в наборі даних сильно корельовані.

Коли це трапляється, модель може добре відповідати навчальному набору даних, але може працювати погано на новому наборі даних, який вона ніколи не бачила, оскільки він переповнює навчальний набір даних. навчальний набір.

Один із способів вирішити цю проблему — використати метод часткових найменших квадратів , який працює наступним чином:

• Стандартизуйте змінні прогнозу та відповіді.
• Обчисліть M лінійних комбінацій (званих «компонентами PLS») p початкових змінних предикторів, які пояснюють значну кількість варіацій як у змінній відповіді, так і в змінних предикторів.
• Використовуйте метод найменших квадратів, щоб підібрати модель лінійної регресії, використовуючи компоненти PLS як предиктори.
• Використовуйте k-кратну перехресну перевірку , щоб знайти оптимальну кількість компонентів PLS для збереження в моделі.

Цей підручник надає покроковий приклад того, як виконувати часткові найменші квадрати в Python.

Крок 1. Імпортуйте необхідні пакети

Спочатку ми імпортуємо пакети, необхідні для виконання часткових найменших квадратів у Python:

 import numpy as np
import pandas as pd
import matplotlib. pyplot as plt
from sklearn. preprocessing import scale 
from sklearn import model_selection
from sklearn. model_selection import RepeatedKFold
from sklearn. model_selection import train_test_split
from sklearn. cross_decomposition import PLSRegression
from sklearn . metrics import mean_squared_error

Крок 2. Завантажте дані

Для цього прикладу ми використаємо набір даних під назвою mtcars , який містить інформацію про 33 різні автомобілі. Ми будемо використовувати hp як змінну відповіді та наступні змінні як предиктори:

• миль на галлон
• дисплей
• лайно
• вага
• qsec

Наступний код показує, як завантажити та відобразити цей набір даних:

 #define URL where data is located
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/mtcars.csv"

#read in data
data_full = pd. read_csv (url)

#select subset of data
data = data_full[["mpg", "disp", "drat", "wt", "qsec", "hp"]]

#view first six rows of data
data[0:6]


        mpg disp drat wt qsec hp
0 21.0 160.0 3.90 2.620 16.46 110
1 21.0 160.0 3.90 2.875 17.02 110
2 22.8 108.0 3.85 2.320 18.61 93
3 21.4 258.0 3.08 3.215 19.44 110
4 18.7 360.0 3.15 3.440 17.02 175
5 18.1 225.0 2.76 3.460 20.22 105

Крок 3. Підберіть часткову модель найменших квадратів

Наступний код показує, як підігнати модель PLS до цих даних.

Зверніть увагу, що cv = RepeatedKFold() вказує Python використовувати перехресну перевірку k-згортки для оцінки продуктивності моделі. Для цього прикладу ми вибираємо k = 10 згорток, повторених 3 рази.

 #define predictor and response variables
X = data[["mpg", "disp", "drat", "wt", "qsec"]]
y = data[["hp"]]

#define cross-validation method
cv = RepeatedKFold(n_splits= 10 , n_repeats= 3 , random_state= 1 )

mse = []
n = len (X)

# Calculate MSE with only the intercept
score = -1*model_selection. cross_val_score (PLSRegression(n_components=1),
n.p. ones ((n,1)), y, cv=cv, scoring=' neg_mean_squared_error '). mean ()    
mse. append (score)

# Calculate MSE using cross-validation, adding one component at a time
for i in np. arange (1, 6):
    pls = PLSRegression(n_components=i)
    score = -1*model_selection. cross_val_score (pls, scale(X), y, cv=cv,
               scoring=' neg_mean_squared_error '). mean ()
    mse. append (score)

#plot test MSE vs. number of components
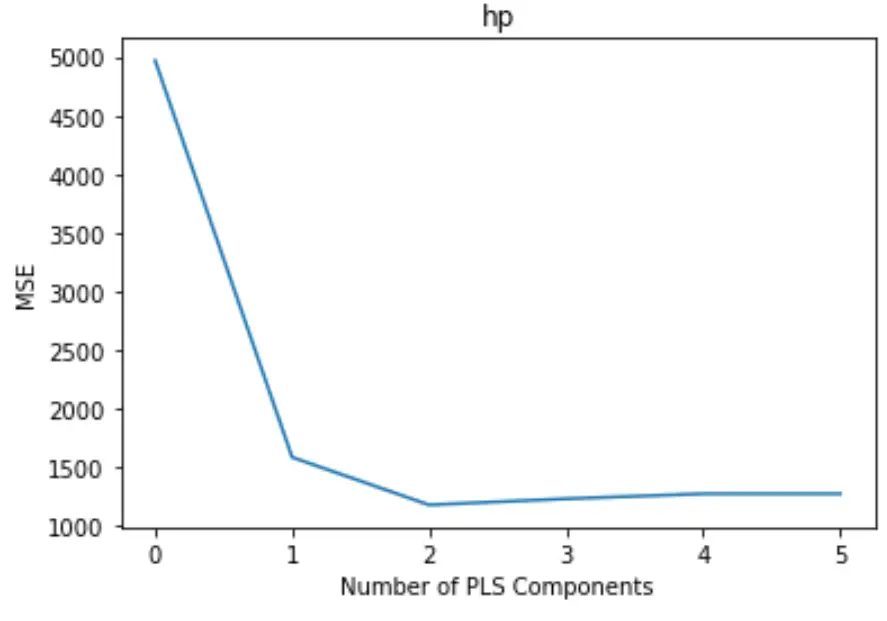
plt. plot (mse)
plt. xlabel (' Number of PLS Components ')
plt. ylabel (' MSE ')
plt. title (' hp ')

На графіку відображається кількість компонентів PLS по осі абсцис і тест MSE (середня квадратична помилка) по осі у.

На графіку ми бачимо, що MSE тесту зменшується при додаванні двох компонентів PLS, але починає збільшуватися, коли ми додаємо більше двох компонентів PLS.

Таким чином, оптимальна модель включає лише перші два компоненти PLS.

Крок 4. Використовуйте остаточну модель для прогнозування

Ми можемо використовувати остаточну модель PLS із двома компонентами PLS, щоб робити прогнози щодо нових спостережень.

У наведеному нижче коді показано, як розділити вихідний набір даних на навчальний і тестовий набір і використовувати модель PLS із двома компонентами PLS для прогнозування на тестовому наборі.

 #split the dataset into training (70%) and testing (30%) sets
X_train , _

#calculate RMSE
pls = PLSRegression(n_components=2)
pls. fit (scale(X_train), y_train)

n.p. sqrt (mean_squared_error(y_test, pls. predict (scale(X_test))))

29.9094

Ми бачимо, що RMSE тесту виявляється 29,9094 . Це середнє відхилення між прогнозованим значенням hp і спостережуваним значенням hp для спостережень тестового набору.

Повний код Python, використаний у цьому прикладі, можна знайти тут .