Незалежна змінна

У цій статті пояснюється, що таке незалежні змінні. Таким чином, ви знайдете значення незалежної змінної в математиці та статистиці, а також побачите кілька прикладів цього типу змінної.

Що таке незалежна змінна?

Незалежна змінна — це змінна, значення якої не залежить від значення будь-якої іншої змінної. Навпаки, якщо незалежна змінна змінює своє значення, вона змінює значення залежної змінної.

Коли ви малюєте графік незалежної змінної, вона зазвичай позначається літерою x і на осі x (горизонтальна вісь).

Наприклад, тривалість оренди нерухомості є незалежною змінною, яка впливає на ціну, яку ви платите. Оскільки тривалість оренди може бути визначена, і її значення впливає на змінну, що залежить від ціни, оскільки чим довше об’єкти використовуються, тим більше вони повинні платити.

Незалежні змінні також можна назвати пояснювальними змінними, вхідними змінними або керованими змінними.

Приклади незалежних змінних

Ознайомившись із визначенням незалежної змінної, давайте тепер розглянемо кілька прикладів цього типу змінної, щоб краще зрозуміти концепцію.

• Час, витрачений на навчання (незалежна змінна), впливає на отримані оцінки (залежна змінна).
• Ціна товару (незалежна змінна) змінює кількість людей, які бажають купити товар (залежна змінна).
• Температура навколишнього середовища (незалежна змінна) впливає на кількість лісових пожеж (залежна змінна).
• Реклама продукту (незалежна змінна) впливає на кількість продажів зазначеного продукту (залежна змінна).
• Кількість жителів міста (незалежна змінна) пов’язана з кількістю таксі в місті (залежна змінна).

Незалежна змінна в математиці

У математиці причинно-наслідковий зв’язок зазвичай моделюється за допомогою незалежної змінної та залежної змінної. Таким чином, функція визначає математичне співвідношення, яке існує між незалежною змінною та залежною змінною.

Незалежні змінні зазвичай позначаються літерою x , тоді як літера y використовується для залежних змінних.

Наприклад, функція y=2x вказує, що коли незалежна змінна x збільшується на одну одиницю, залежна змінна y збільшується вдвічі більше.

Щоб дізнатися більше про математичні функції, ми рекомендуємо відвідати веб-сайт нашого партнера function.xyz .

Незалежні змінні в статистиці

Однак насправді дуже важко знайти зв’язок між двома змінними, який можна визначити точною математичною функцією, тому що іноді те саме значення незалежної змінної призводить до іншого значення залежної змінної.

Наприклад, іноді, навчаючись більше, ми отримуємо нижчу оцінку або, навпаки, навчаючись менше, ми отримуємо кращу оцінку. Таким чином, кількість годин, які ми витрачаємо на навчання, не є єдиним фактором, який впливає на отриману оцінку, вона також може змінюватися залежно від складності іспиту або складності предмета, що вивчається.

Тому в статистиці зазвичай проводять багато експериментів, щоб визначити, чи існує зв’язок між незалежною змінною та залежною змінною. Потім отримані результати можна представити графічно, щоб перевірити, чи зв’язані змінні, і, якщо так, побачити, який тип зв’язку вони мають (позитивний, негативний, лінійний, експоненціальний тощо).

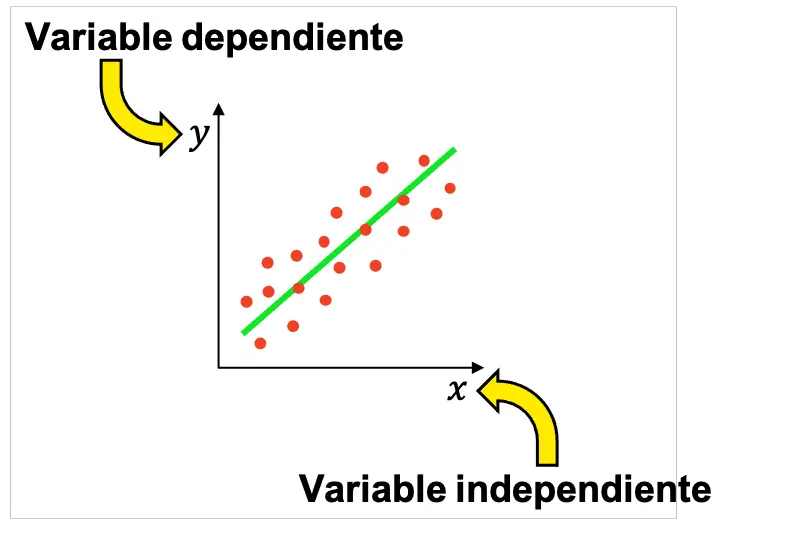
Майте на увазі, що в опитуванні може бути більше однієї незалежної змінної, хоча основні статистичні дослідження проводяться з однією незалежною та однією залежною змінною.

Після проведення статистичного дослідження можна обчислити математичну функцію, яка дає змогу зробити наближення та таким чином змоделювати зв’язок між змінними. Тож зазвичай ви спочатку створюєте статистичну модель, а потім математичну.