4 приклади відсутності кореляції між змінними

У статистиці кореляція є мірою лінійного зв’язку між двома змінними.

Значення коефіцієнта кореляції завжди між -1 і 1, де:

• -1 вказує на абсолютно негативну лінійну кореляцію між двома змінними
• 0 означає відсутність лінійної кореляції між двома змінними
• 1 вказує на абсолютно позитивну лінійну кореляцію між двома змінними

Якщо кореляція двох змінних дорівнює нулю, це означає, що вони жодним чином не пов’язані. Іншими словами, знання значення однієї змінної не дає нам уявлення про те, яким може бути значення іншої змінної.

Якщо ми створимо діаграму розсіювання двох змінних, які мають нульову кореляцію, на графіку не буде чіткої закономірності:

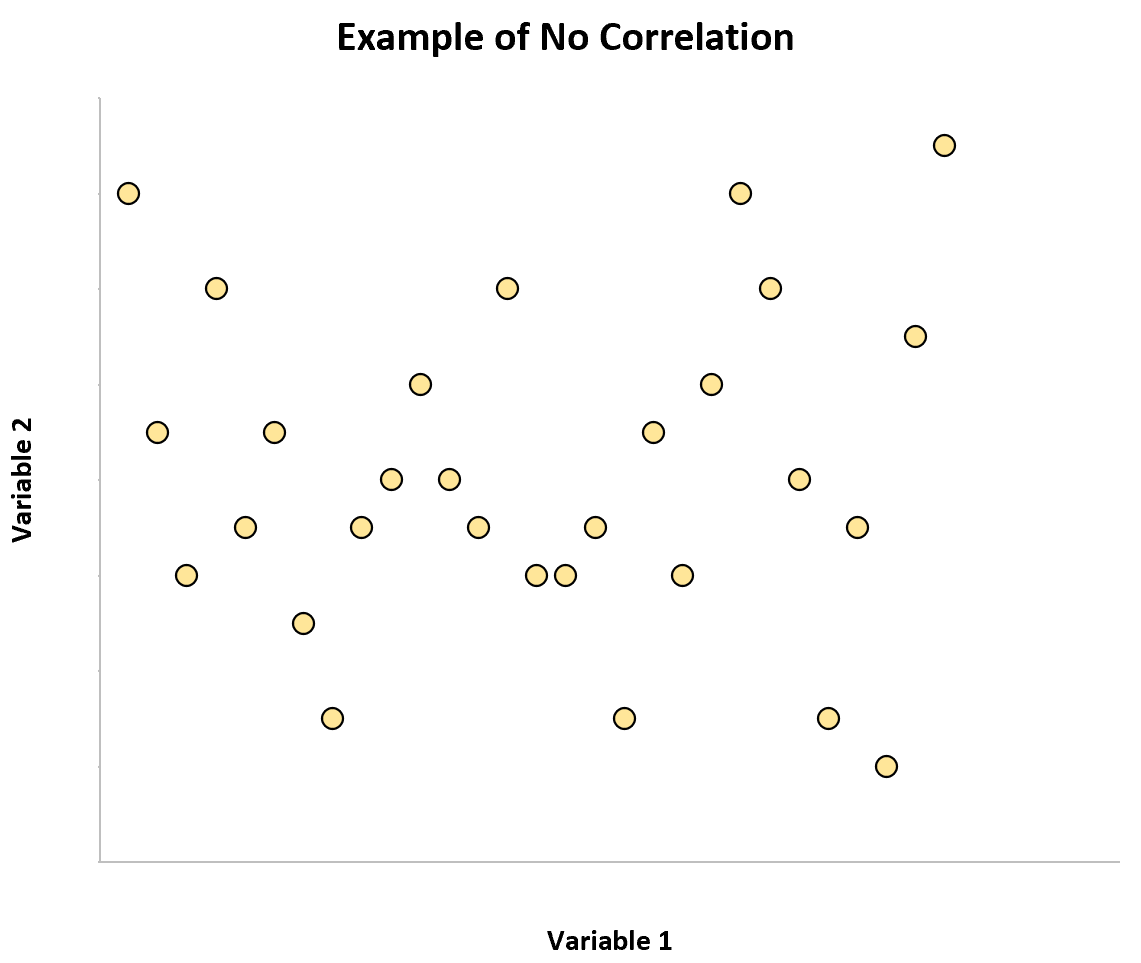
Приклади відсутності кореляції

Наступні приклади ілюструють сценарії, у яких дві змінні не мають кореляції.

Приклад 1: Споживання кави проти інтелекту

Кількість спожитої людиною кави та рівень її IQ не мають нульової кореляції. Іншими словами, знання того, скільки кави випиває людина, не дає нам уявлення про рівень її IQ.

Якби ми побудували діаграму розсіювання щоденного споживання кави в порівнянні з рівнем IQ, це виглядало б так:

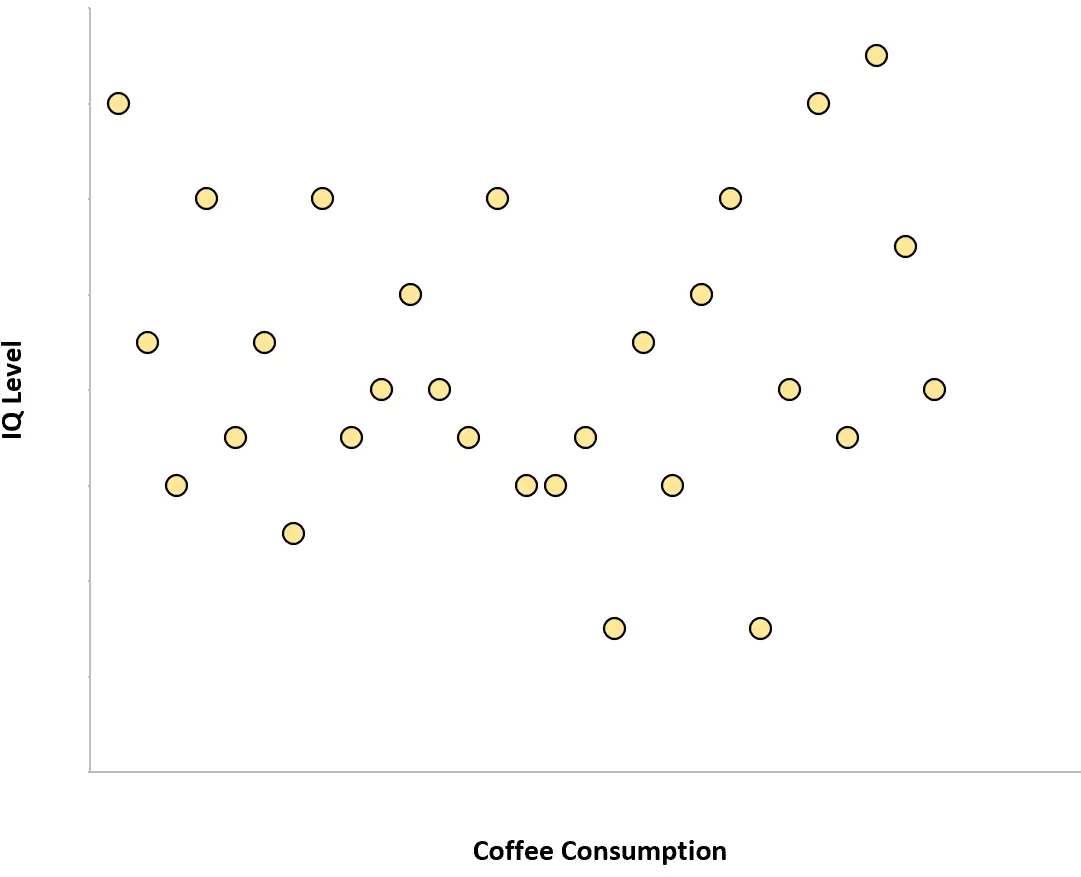
Приклад 2: Зріст і тестові результати

Зріст учнів та їх середній тестовий бал кореляція дорівнює нулю. Іншими словами, знання зросту людини не дає нам уявлення про її середній іспитовий бал.

Якби ми створили діаграму розсіювання, що відображає зріст і середній бал за іспит, це виглядало б так:

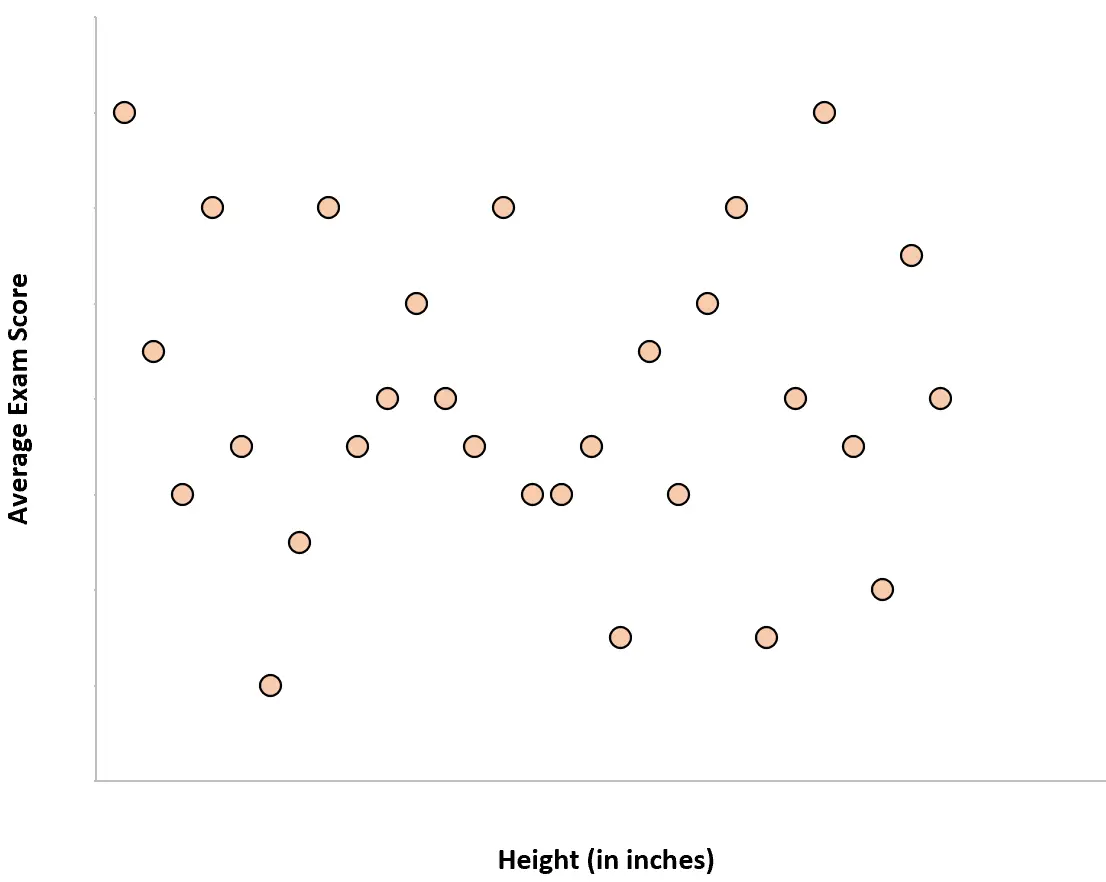
Приклад 3: розмір взуття та переглянуті фільми

Розмір взуття людей і кількість фільмів, які вони дивляться на рік, не мають нульової кореляції. Іншими словами, знання розміру взуття людини не дає нам уявлення про те, скільки фільмів вона дивиться на рік.

Якби ми створили точкову діаграму залежності розміру взуття від кількості переглянутих фільмів, це виглядало б так:

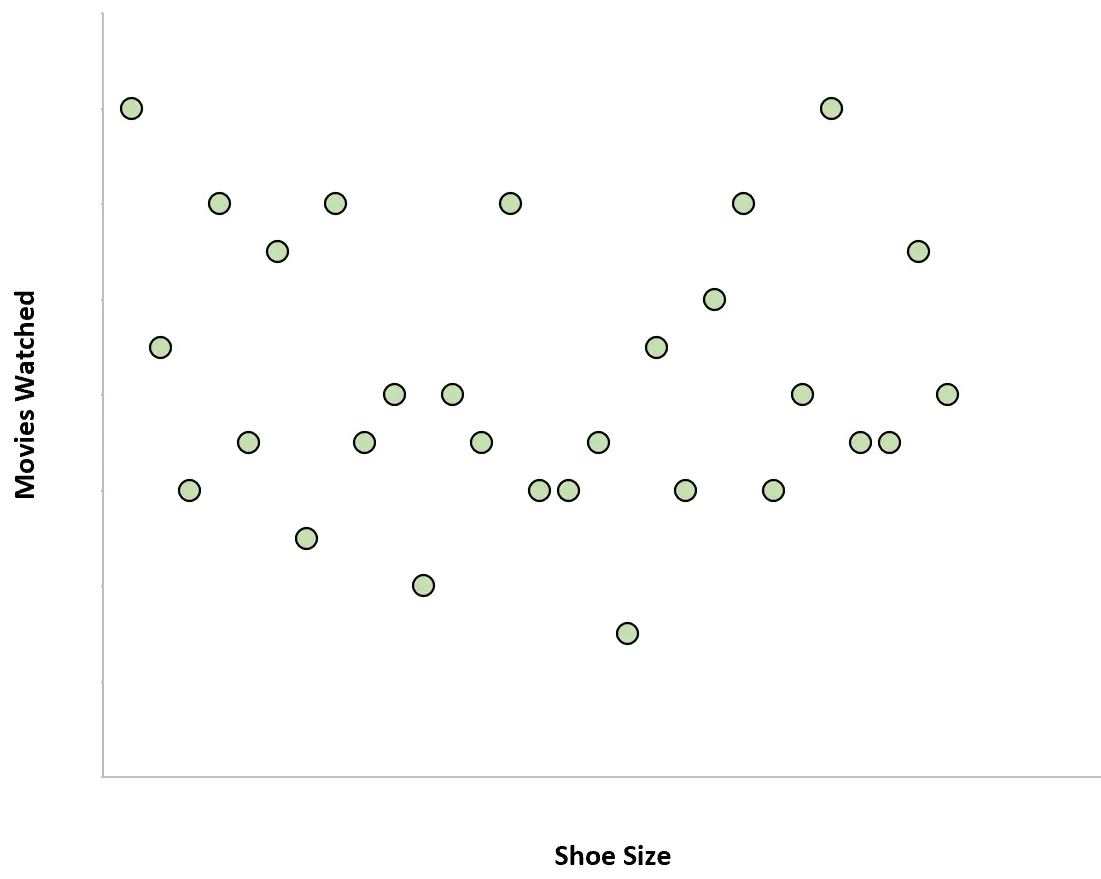
Приклад 4: вага і дохід

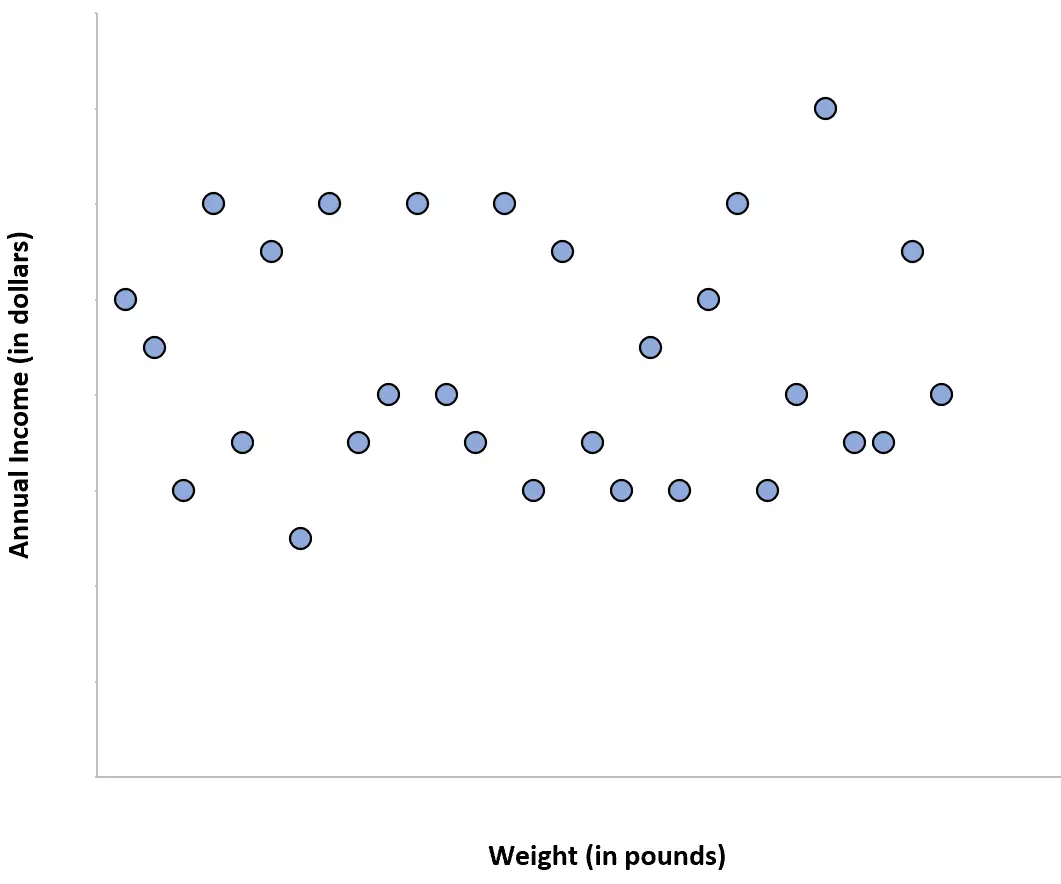
Вага фізичних осіб та їхній річний дохід мають нульову кореляцію. Іншими словами, знання ваги людини не дає нам уявлення про те, яким може бути її річний дохід.

Якби ми створили діаграму розкиду ваги/доходу, вона виглядала б так:

Додаткові ресурси

Вступ до коефіцієнта кореляції Пірсона
Кореляція vs. асоціація: яка різниця?
Кореляція проти регресії: у чому різниця?