Нормальний розподіл і стандартний нормальний розподіл: різниця

Нормальний розподіл є найбільш часто використовуваним розподілом ймовірностей у статистиці.

Він має такі властивості:

• Симетричний
• У формі дзвоника
• Середнє та медіана рівні; обидва розташовані в центрі розподілу

Середнє значення нормального розподілу визначає його розташування, а стандартне відхилення визначає його поширення.

Наприклад, на наступному графіку показано три нормальних розподілу з різними середніми значеннями та стандартними відхиленнями:

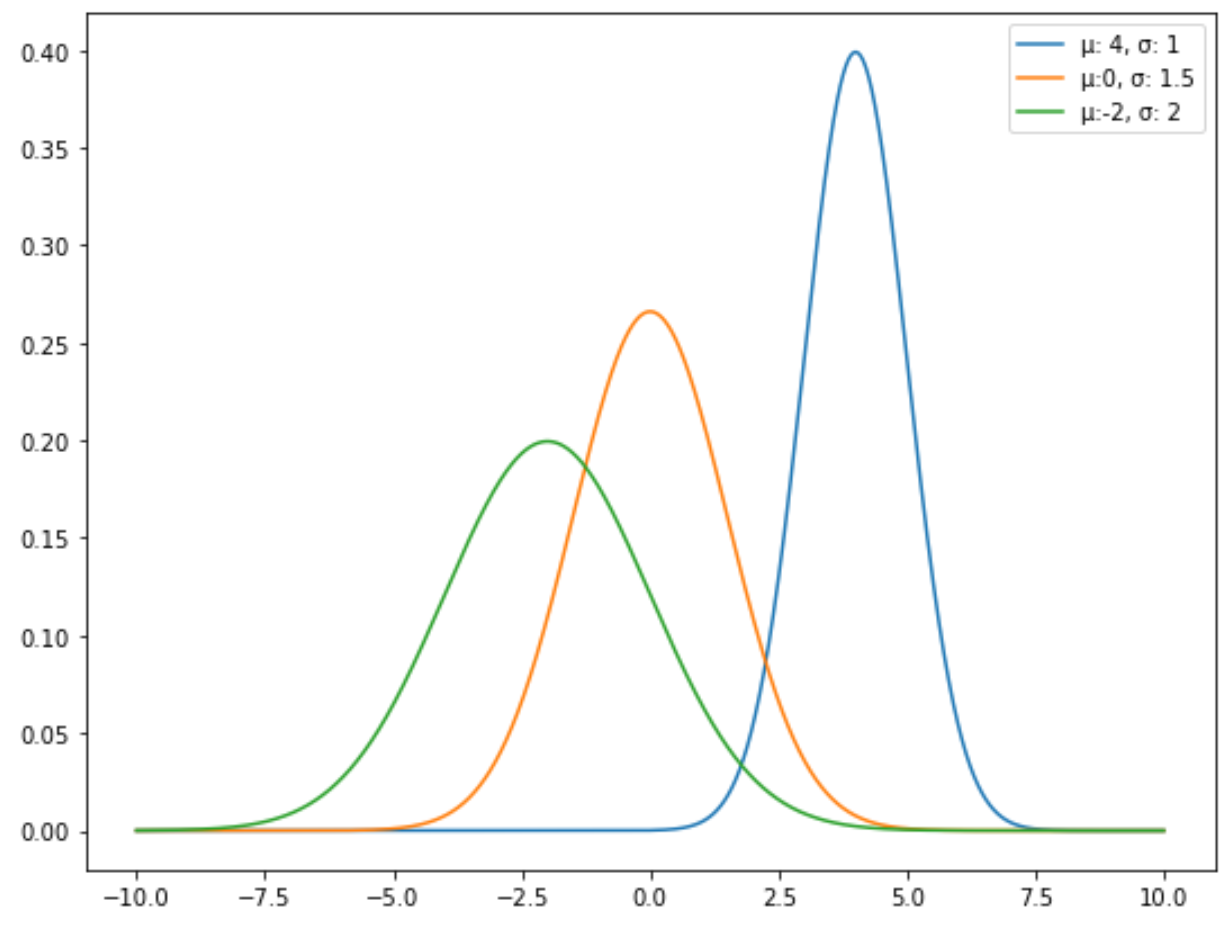
Стандартний нормальний розподіл — це певний тип нормального розподілу, де середнє значення дорівнює 0, а стандартне відхилення — 1.

На наступному графіку показано стандартний нормальний розподіл:

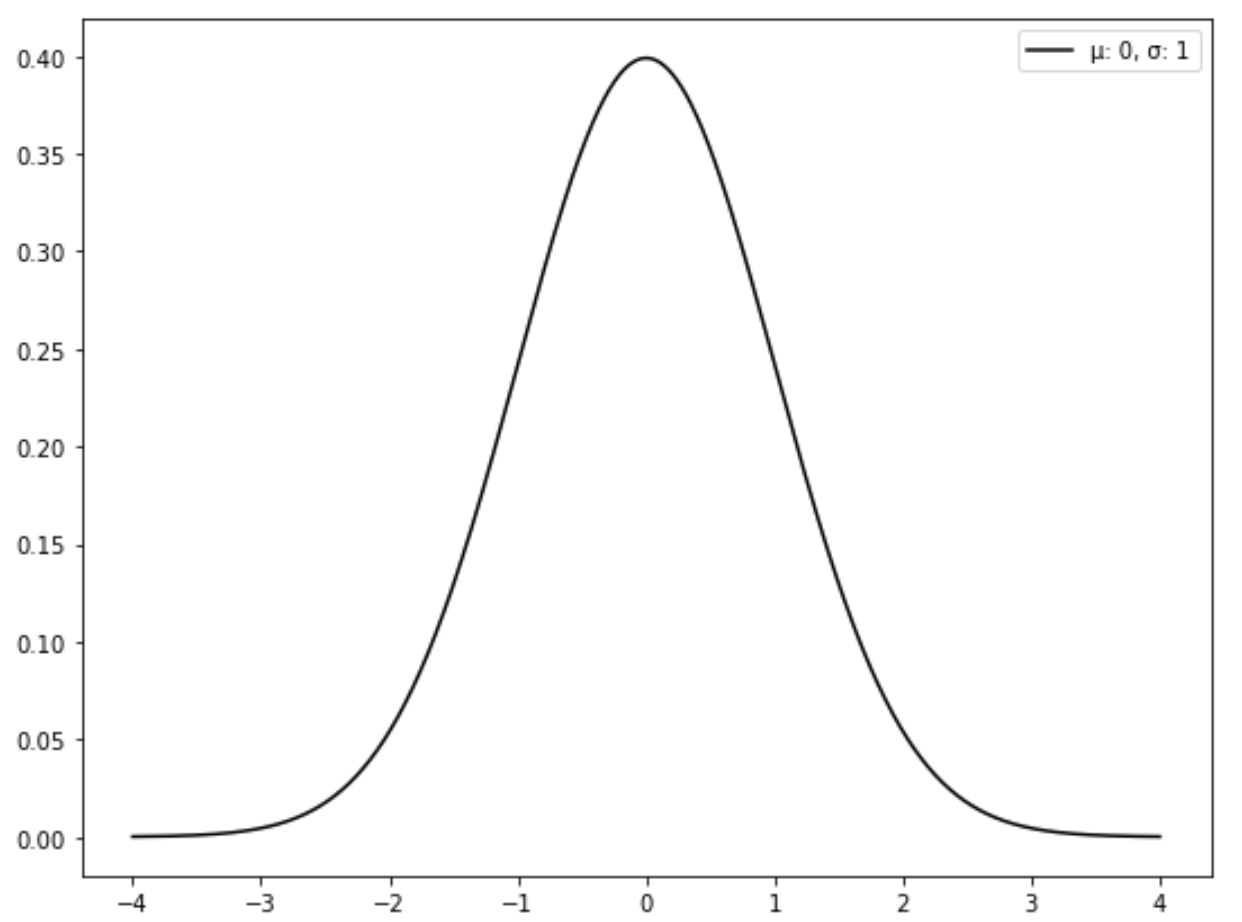
Як перетворити нормальний розподіл на стандартний нормальний розподіл

Будь-який нормальний розподіл можна перетворити на стандартний нормальний розподіл шляхом перетворення значень даних у z-показники за такою формулою:

z = (x – μ) / σ

золото:

• x: значення індивідуальних даних
• μ: середнє значення розподілу
• σ: стандартне відхилення розподілу

Наприклад, припустімо, що ми маємо такий набір даних із середнім значенням 6 і стандартним відхиленням 2,152:

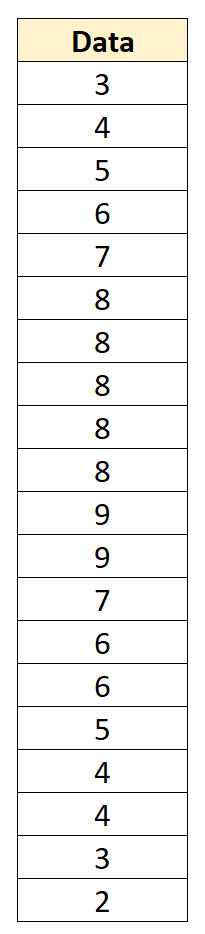
Ми можемо перетворити кожне окреме значення даних у z-показник, віднявши 6 від кожного значення та поділивши на 2,152:

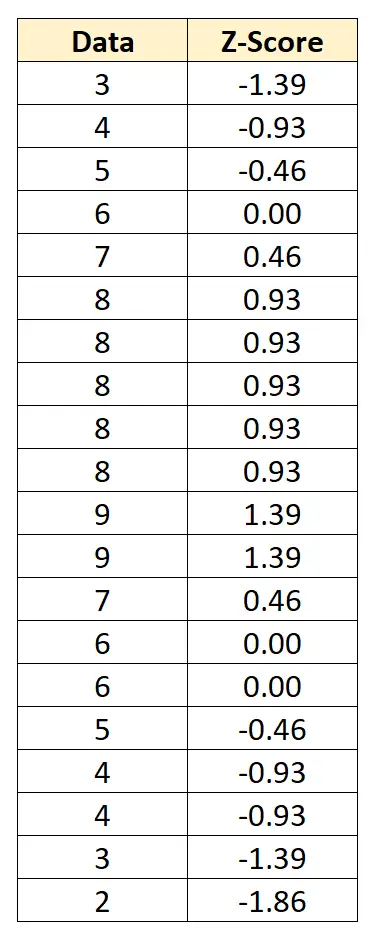
Z-показник говорить нам, скільки стандартних відхилень кожна точка даних має від середнього. Наприклад, перше значення даних «3» на 1,39 стандартних відхилень нижче середнього.

Середнє значення цього розподілу балів має середнє значення нуль і стандартне відхилення одиниці.

Як використовувати стандартний нормальний розподіл

Стандартний нормальний розподіл має такі властивості:

• Близько 68% даних знаходяться в межах одного стандартного відхилення від середнього
• Близько 95% даних знаходяться в межах двох стандартних відхилень від середнього.
• Близько 99,7% даних знаходяться в межах трьох стандартних відхилень від середнього.

Це відоме як емпіричне правило , яке використовується для розуміння розподілу значень у наборі даних.

Наприклад, припустимо, що висота рослин у певному саду зазвичай розподілена із середнім значенням 47,4 дюйма та стандартним відхиленням 2,4 дюйма.

Використовуючи емпіричне правило, який відсоток рослин має висоту менше 54,6 дюйма?

Емпіричне правило стверджує, що для заданого набору даних із нормальним розподілом 99,7% значень даних знаходяться в межах трьох стандартних відхилень від середнього. Це означає, що 49,85% значень знаходяться між середнім і трьома стандартними відхиленнями вище середнього.

У цьому прикладі 54,6 — це три стандартні відхилення вище середнього. Оскільки ми знаємо, що 50% значень даних є меншими за середнє у нормальному розподілі, загалом 50% + 49,85% = 99,85% значень є меншими за 54,6.

Таким чином, 99,85% рослин мають висоту менше 54,6 дюймів.

Додаткові ресурси

Проблеми у вивченні емпіричних правил
Правила калькулятора
Як застосувати емпіричне правило в Excel