Стандартний нормальний розподіл

за Редакція 4 Серпня, 2023 Ймовірність 0 коментарів

У цій статті пояснюється, що таке стандартний нормальний розподіл і для чого він використовується. Ви також знайдете властивості стандартного нормального розподілу, таблицю з його характерними значеннями та, крім того, розв’язану вправу.

Що таке стандартний нормальний розподіл?

Стандартний нормальний розподіл , який також називають одиничним нормальним розподілом , є найпростішим випадком нормального розподілу. Точніше, стандартний нормальний розподіл – це нормальний розподіл із середнім значенням і стандартним відхиленням, що дорівнює 0 і 1 відповідно.

Таким чином, стандартний нормальний розподіл визначається як N(0,1), де перший параметр — це середнє значення розподілу, а другий параметр — його стандартне відхилення (або SD).

$\displaystyle N(0,1) \ \color{orange}\bm{\longrightarrow}\color{black}\begin{cases} \mu=0\\[2ex]\sigma=1\end{cases}$

Отже, графік стандартного нормального розподілу має такий вигляд:

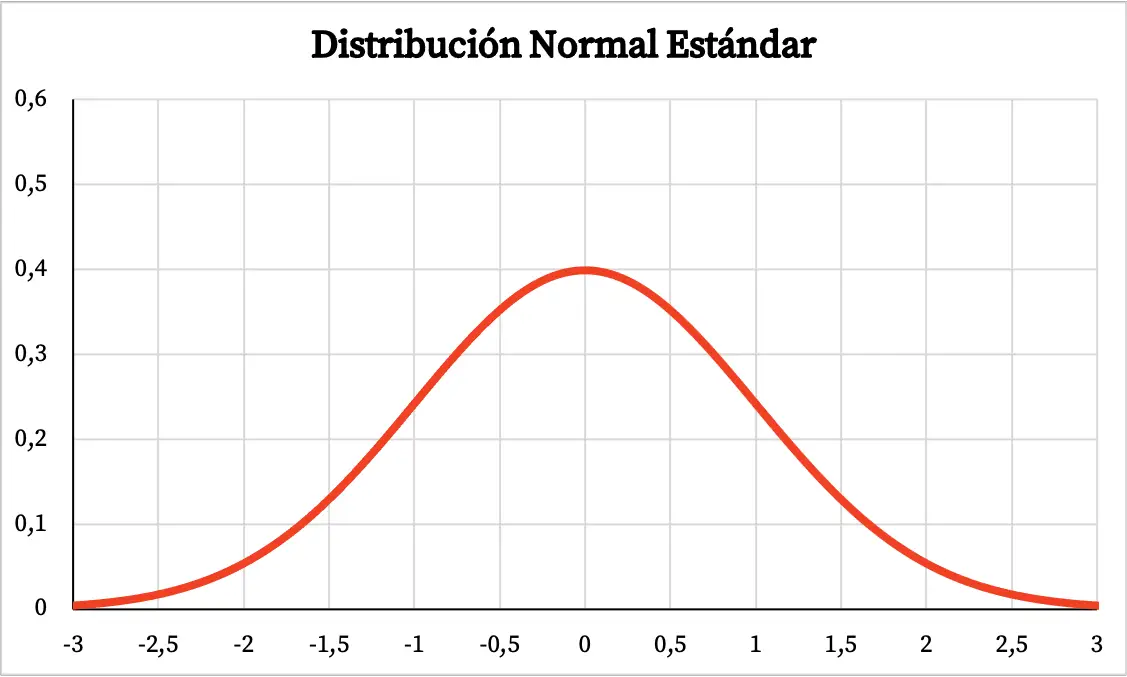
Формула стандартного нормального розподілу

Щоб перетворити будь-який нормальний розподіл у стандартний нормальний розподіл, ви повинні відняти середнє значення нормального розподілу від усіх його значень, а потім розділити на стандартне відхилення нормального розподілу.

Таким чином , формула стандартного нормального розподілу має такий вигляд:

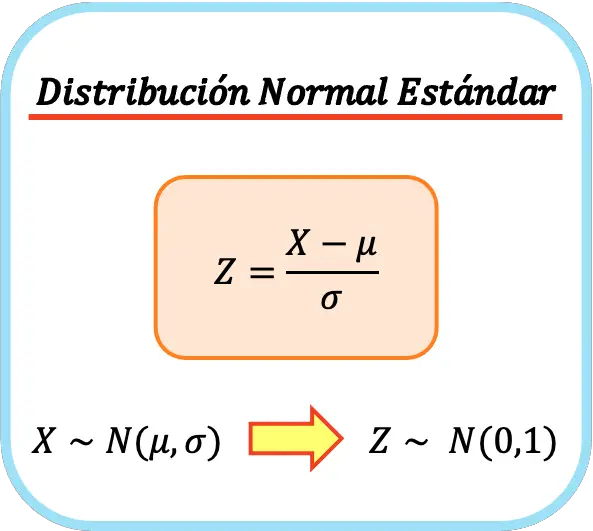
стандартна формула нормального розподілу

Таким чином, середнє арифметичне та стандартне відхилення нової змінної будуть 0 і 1 відповідно, тому ми отримаємо стандартний нормальний розподіл. Цей процес також називають однофакторною нормалізацією або однофакторною нормалізацією .

Стандартна таблиця нормального розподілу

Таблиця стандартного нормального розподілу — це таблиця, яка містить ймовірності того, що спостережуване значення менше заданого значення стандартного нормального розподілу.

Крім того, оскільки функція нормального розподілу залежить від його середнього значення та стандартного відхилення, таблиця стандартного нормального розподілу також використовується, як розширення, для визначення ймовірностей будь-якого нормального розподілу. Для цього нормальний розподіл вписуємо в стандартний нормальний розподіл і потім дивимося в таблиці, яка ймовірність йому відповідає.

Отже, значення в стандартній таблиці нормального розподілу наступні:

стандартна таблиця нормального розподілу

Приклад стандартного нормального розподілу

Тепер, коли ми знаємо визначення стандартного нормального розподілу та його формулу, нижче наведено конкретний приклад, щоб добре зрозуміти концепцію.

Безперервна випадкова змінна відповідає нормальному розподілу із середнім значенням 45 і стандартним відхиленням 15. Яка ймовірність отримати значення, менше або дорівнює 58?

$N(45,15)\ \color{orange}\bm{\longrightarrow}\color{black}\ P[X\leq 58]= \ \color{orange}\bm{?}\color{black}$

Щоб знайти ймовірність нормального розподілу, нам потрібно використати його таблицю ознак, але для цього нам спочатку потрібно виконати процес введення, щоб отримати стандартний нормальний розподіл. Тому ми використовуємо стандартну формулу нормального розподілу:

$Z=\cfrac{X-\mu}{\sigma}$

Тому ми віднімаємо середнє значення від значення ймовірності, а потім ділимо на стандартне відхилення

$\displaystyle P[X\leq 58]=P\left[Z\leq\frac{58-45}{15}\right]=P[Z\leq 0,87]$

Після того, як ми стандартизували змінну, ми переходимо до стандартної таблиці ймовірностей нормального розподілу (див. вище), щоб побачити, якій ймовірності відповідає значення 0,87:

$\displaystyle P[Z\leq 0,87]=0,8078$

Таким чином, ймовірність отримати значення, рівне або менше 58, становить 80,78%.

Характеристики стандартного нормального розподілу

Стандартний нормальний розподіл має такі характеристики:

Стандартний нормальний розподіл — це симетричний розподіл із центром 0.
Подібно до нормального розподілу, стандартний графік нормального розподілу має форму дзвона, при цьому більша частина площі графіка знаходиться навколо середнього значення.
Тому середнє, мода та медіана нормального розподілу мають однакове значення, яке дорівнює 0.
Стандартний нормальний розподіл має максимум при z=0.
Подібним чином стандартний нормальний розподіл має дві точки перегину при z=-1 і z=+1.
Згідно з емпіричним правилом, ми знаємо, що 68% значень потрапляють у стандартний нормальний розподіл між +1 і -1, 95% значень між +2 і -2 і 99,7% значень між + 3 і – 3.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше