Що таке обмеження обсягу?

Часто в статистиці ми прагнемо виміряти кореляцію між двома змінними. Це допомагає нам зрозуміти наступне:

• Напрямок зв’язку між двома змінними. Коли одна змінна збільшується, інша змінна має тенденцію до збільшення чи зменшення?
• Сила зв’язку між двома змінними. Наскільки зміниться значення двох змінних?

На жаль, проблема, яка може виникнути під час вимірювання кореляції між двома змінними, називається обмеженням діапазону . Це відбувається, коли діапазон виміряних значень для однієї зі змінних з якоїсь причини обмежений.

Наприклад, припустімо, що ми хочемо виміряти співвідношення між навчальними годинами та результатами іспитів учнів певної школи.

Якщо ми зберемо дані щодо цих двох змінних для всіх 1000 учнів у школі, ми можемо виявити, що кореляція між годинами навчання та результатами іспитів становить 0,73 .

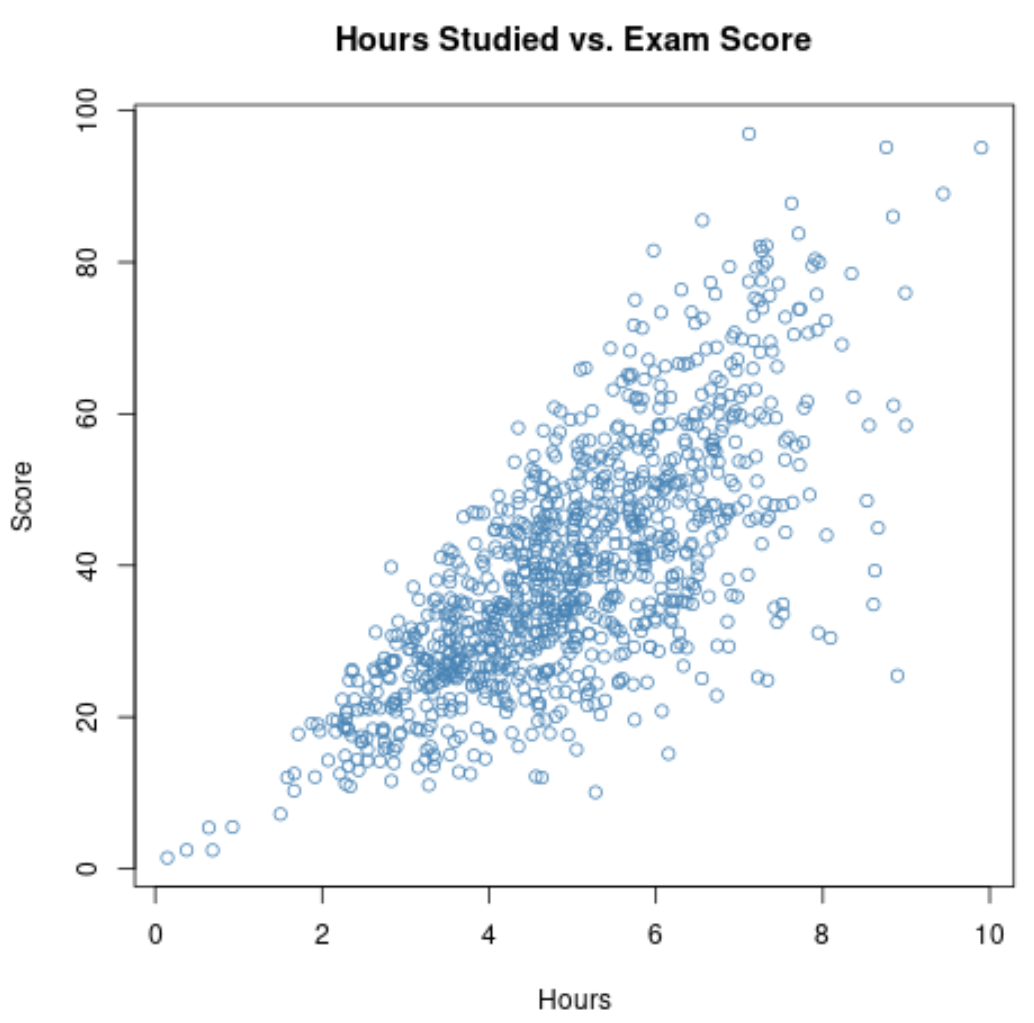
Ця кореляція досить висока, що вказує на сильний позитивний зв’язок між двома змінними. Чим більше студенти навчаються, тим краще вони успішно складають іспити.

Однак припустімо, що ми збираємо дані лише про студентів курсів із відзнакою. Цілком можливо, що всі ці студенти навчалися щонайменше 6 годин.

Отже, якщо ми обчислимо співвідношення між годинами вивчення та результатами іспитів для цих студентів, ми використаємо вузький діапазон для змінних годин навчання .

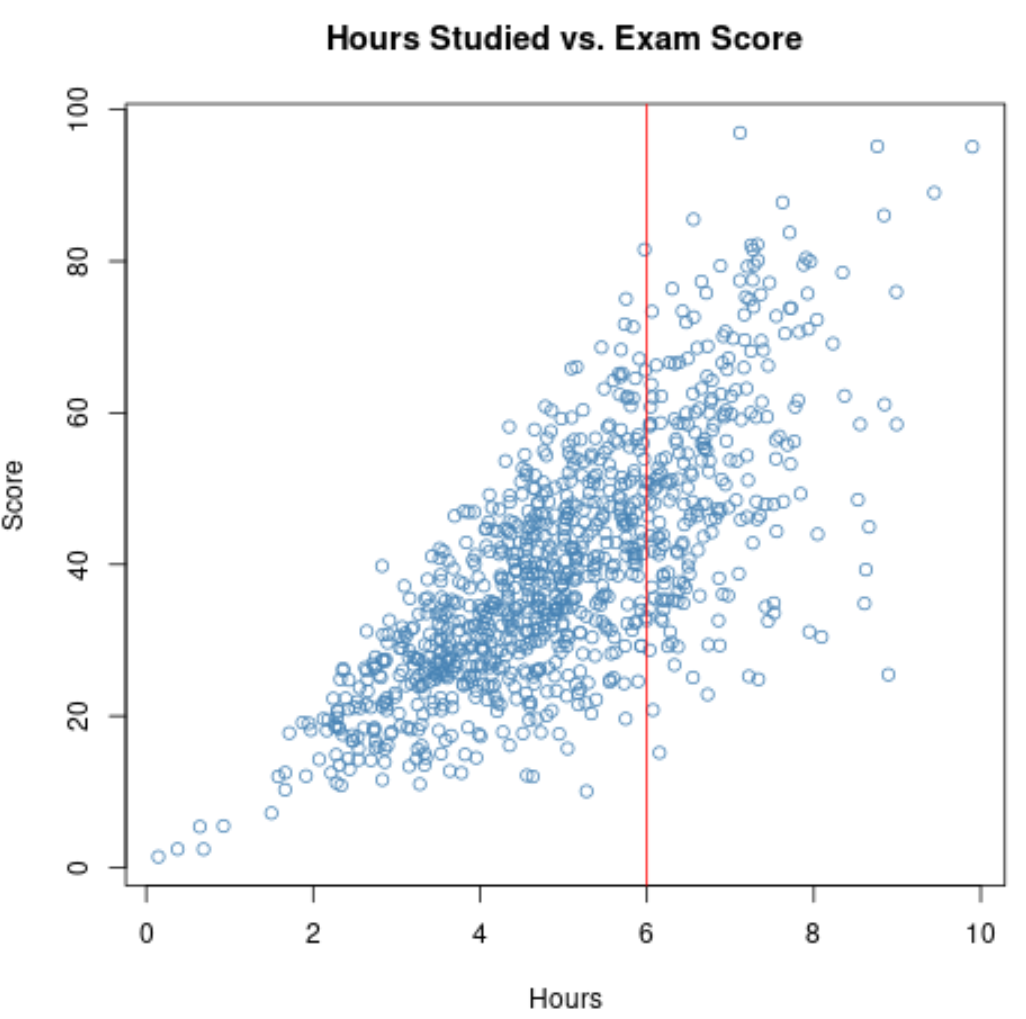
Якщо ми збільшимо масштаб діаграми розсіювання для діапазону, де кількість годин перевищує 6, то вона виглядатиме ось як:

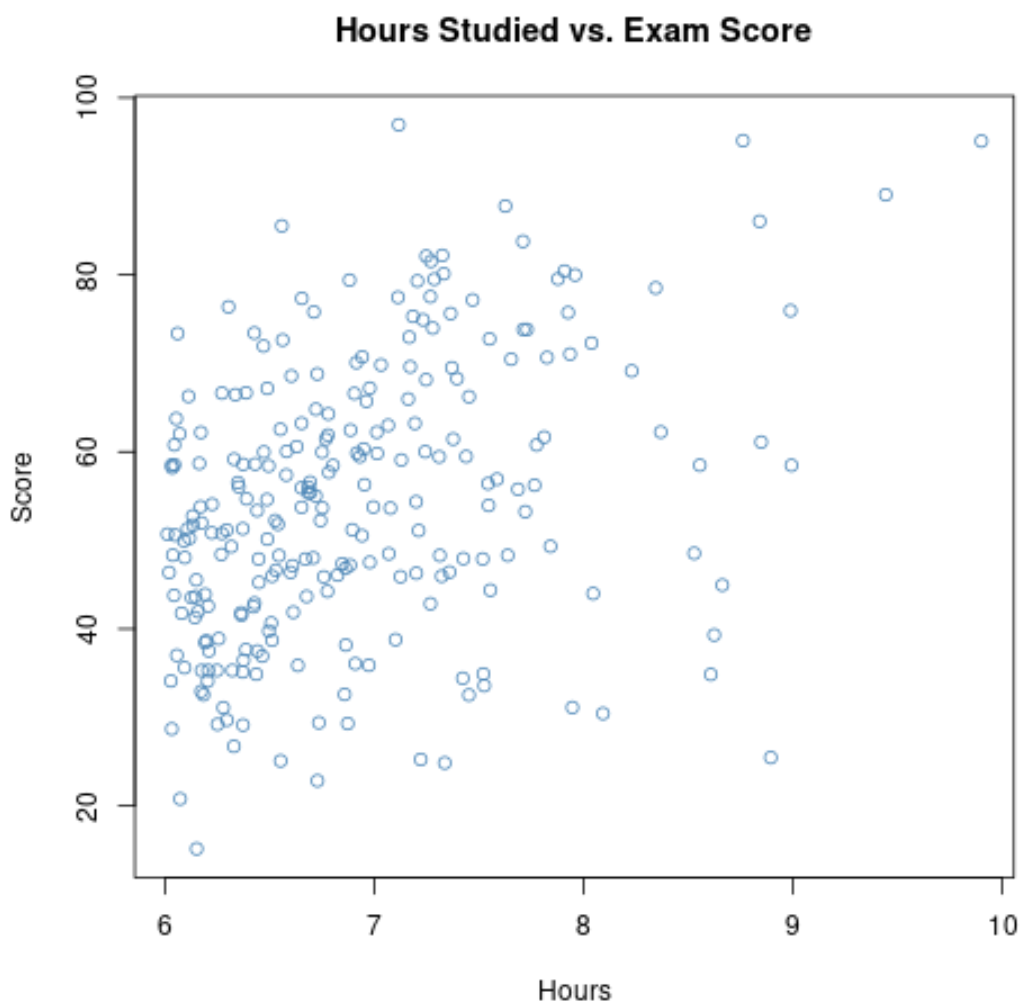
Кореляція між двома змінними на цьому графіку дорівнює 0,37 , що значно менше, ніж 0,73 .

Таким чином, якби ми збирали лише дані про вивчені години та оцінки за іспити для студентів курсів із відзнакою, ми могли б припустити, що існує слабкий зв’язок між годинами навчання та оцінками за іспит.

Однак цей результат вводить в оману, оскільки ми використовували обмежений діапазон для однієї зі змінних.

Реальні приклади обмеженого діапазону

Проблема обмеженого діапазону може виникнути на практиці в багатьох різних дослідженнях. Ось кілька прикладів:

1. Дослідження високопродуктивних спортсменів . Дослідникам може бути цікаво вивчити, чи певна тренувальна програма створює більше м’язової маси, ніж певна стандартна програма.

Якщо дослідники збирають дані лише про елітних спортсменів, цілком ймовірно, що всі ці спортсмени вже мають велику м’язову масу. Таким чином, буде доступний вузький діапазон значень для розрахунку кореляції між програмою тренувань і виробленою м’язовою масою.

2. Дослідження успішних учнів. Дослідники можуть захотіти вивчити, чи позитивно впливає певна програма репетиторства на оцінки. За своєю природою студенти, які прагнуть покращити свої оцінки та взяти участь у програмі репетиторства, можуть уже бути студентами з високими досягненнями.

Тож оцінки цих студентів, можливо, не мають багато чого для покращення. Коли дослідники обчислюють кореляцію між годинами, проведеними в програмі репетиторства, і результуючим підвищенням оцінки, справжня кореляція може бути недооцінена, оскільки простір для підвищення оцінки був обмежений.

Як враховувати обмежені діапазони

Популярний спосіб обліку обмежених діапазонів відомий як випадок Торндайка 2 , формула, розроблена психометриком Робертом Л. Торндайком.

Ця формула надає оцінку справжньої кореляції між двома змінними та використовує такі обчислення:

Справжня кореляція = √(1-(SD ² _{y обмежений} -SD ² _{y необмежений} )) * (1-r ² _{обмежений} )

золото:

• SD ² _{restricted y} : Квадрат стандартного відхилення доступних даних для змінної відповіді y.
• _{Необмежене} SD ² y: відомий квадрат стандартного відхилення змінної відповіді для сукупності.
• r ² _restricted : Квадратична кореляція на доступних обмежених даних.

Показано, що ця формула є ефективною для отримання неупереджених оцінок справжньої кореляції між двома змінними, коли одна зі змінних страждає від обмеженого діапазону.

Зауважте, що для використання цієї формули ви повинні мати оцінку справжнього стандартного відхилення сукупності для змінної відповіді.