Обсяг вибірки

за Редакція 3 Серпня, 2023 Статистика 0 коментарів

У цій статті пояснюється, що таке розмір вибірки та чому він важливий у статистиці. Крім того, ви дізнаєтеся, як розрахувати відповідний розмір вибірки, і розв’яжете вправу, щоб побачити, як це робиться.

Який розмір вибірки?

Розмір вибірки (або обсяг вибірки ) — це кількість осіб, які складають вибірку дослідження. У статистиці розмір вибірки важливий, щоб вибірка була репрезентативною для всієї сукупності.

Тому розмір вибірки статистичного дослідження має бути достатньо великим, щоб відображати характеристики всієї сукупності. З іншого боку, розмір вибірки не може бути надмірно великим, оскільки тоді дослідження стає дорожчим. Підсумовуючи, розмір вибірки має бути адекватним, не надто великим і не надто малим.

Наприклад, якщо ми хочемо провести аналіз висоти країни, ми не можемо запитати зріст усіх жителів країни, тому що дослідження займе багато часу і буде надто дорогим. Тому необхідно проводити випадкову вибірку та опитувати лише репрезентативну вибірку населення.

➤ Див.: Типи вибірки

І як ми можемо дізнатися відповідний розмір вибірки? У наступному розділі ми побачимо, як визначити відповідний розмір вибірки на основі вимог дослідження.

Як розрахувати розмір вибірки

Для оцінки середнього значення необхідний розмір вибірки дорівнює квадрату Z _α/2 , помноженому на стандартне відхилення (σ), поділеному на бажану похибку (e). Отже , формула для розрахунку розміру вибірки така:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

золото:

$n$

це розмір вибірки.
$\alpha$

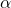
це бажаний рівень значущості. Беручи до уваги це

$1-\alpha$

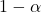
це бажаний рівень впевненості.
$Z_{\alpha/2}$

квантиль стандартного нормального розподілу, що відповідає ймовірності α/2. Для великих розмірів вибірки та 95% рівня довіри він зазвичай близький до 1,96, а для 99% рівня довіри він зазвичай близький до 2,576.
$\sigma$

є стандартним відхиленням.

Майте на увазі, що в цій формулі передбачається, що чисельність популяції нескінченна, тобто чисельність популяції дуже велика або невідома.

Примітка. Наведену вище формулу отримано з інтервалу формули довірчого значення для середнього значення .

Приклад розрахунку обсягу вибірки

У цьому розділі ми розрахуємо відповідний розмір вибірки для статистичного опитування як приклад.

Ми знаємо, що стандартне відхилення генеральної сукупності становить приблизно 15, але ми не знаємо його середнього значення, тому ми хочемо провести дослідження, щоб оцінити середнє значення. Який розмір вибірки нам потрібен, якщо ми хочемо мати похибку ±2 з рівнем довіри 95%?

Як ми бачили вище, формула для розрахунку розміру вибірки така:

$\displaystyle n=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2$

У цьому випадку бажаний рівень достовірності становить 95%, тому відповідне значення Z _α/2 дорівнює 1,96.

$1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025$

$\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}$

➤ Дивіться: Таблиця зі значеннями рівня достовірності

Нарешті, тепер, коли ми знаємо, скільки коштують усі параметри, ми підставляємо їх значення у формулу та обчислюємо розмір вибірки:

$\begin{aligned}\displaystyle n&=\left(\frac{Z_{\alpha/2}\cdot\sigma}{e}\right)^2\\[2ex] n&=\left(\frac{1,96\cdot 15}{2}\right)^2\\[2ex] n&=216,09 \approx 217 \end{array}$

Коротше кажучи, щоб оцінити середнє значення популяції з бажаними вимогами, нам потрібна принаймні вибірка з 217 особин.

Розмір вибірки, рівень достовірності та похибка

Залежно від рівня достовірності та необхідної похибки необхідний розмір вибірки буде різним. Таким чином, розмір вибірки, рівень достовірності та допустима похибка співвідносяться наступним чином:

Розмір вибірки та рівень довіри прямо пропорційні. Тобто, якщо рівень довіри зростає, розмір вибірки також буде збільшуватися.
Розмір вибірки та похибка обернено пропорційні. Отже, якщо межа похибки збільшується, розмір вибірки зменшиться.
Таким чином, збільшення розміру вибірки може збільшити рівень достовірності або зменшити межу похибки.

Інші формули розміру вибірки

Залежно від параметра, який необхідно оцінити, формула для необхідного розміру вибірки дещо змінюється. Тому в цьому розділі ми побачимо інші формули, які можуть бути корисними для розрахунку розміру вибірки в деяких особливих випадках.

розмір вибірки пропорції

Формула для обчислення розміру вибірки, необхідної для оцінки частки (p), така:

$n=\cfrac{N\cdot Z_{\alpha/2}^2\cdot p\cdot (1-p)}{e^2\cdot (N-1)+Z_{\alpha/2}^2\cdot p\cdot (1-p)}$

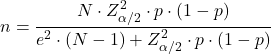
Розмір вибірки ймовірності

Якщо ви хочете оцінити ймовірність, рекомендується використовувати таку формулу для визначення необхідного розміру вибірки:

$\displaystyle n=\left(\frac{Z_{\alpha/2}}{2\cdot e}\right)^2$

Розмір вибірки для порівняння двох незалежних середніх

Формула для розрахунку розміру вибірки при порівнянні двох незалежних середніх із заданим ризиком α та ризиком β виглядає наступним чином:

$n=\cfrac{2\cdot \sigma^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

золото

$\Delta$

це різниця між двома засобами альтернативної гіпотези.

Розмір вибірки для порівняння двох парних середніх

Якщо ви хочете порівняти два парні середні з фіксованою похибкою α і похибкою β, формула, яка буде використана для визначення кількості спостережень у вибірці:

$n=\cfrac{2\cdot \sigma_d^2 \cdot \left(Z_{\alpha/2}+Z_\beta\right)}{\Delta^2}$

золото

$\Delta$

це різниця між двома парними засобами альтернативної гіпотези і

$\sigma_d^2$

Це дисперсія відмінностей між двома вимірюваннями однієї особини.

Про автора

Редакція

Привіт, я Бенджамін, професор статистики на пенсії, який став викладачем статистики. Маючи великий досвід і знання в галузі статистики, я готовий поділитися своїми знаннями, щоб розширити можливості студентів через Statorials. Дізнайтеся більше