Як виконати одновибірковий t-тест у spss

Одновибірковий t-критерій використовується, щоб перевірити, чи дорівнює середнє значення сукупності певному значенню.

У цьому підручнику пояснюється, як виконати одновибірковий t-тест у SPSS.

Приклад: одновибірковий t-тест у SPSS

Ботанік хоче знати, чи дорівнює середня висота певного виду рослин 15 дюймам. Вона бере випадкову вибірку з 12 рослин і записує кожну їх висоту в дюймах:

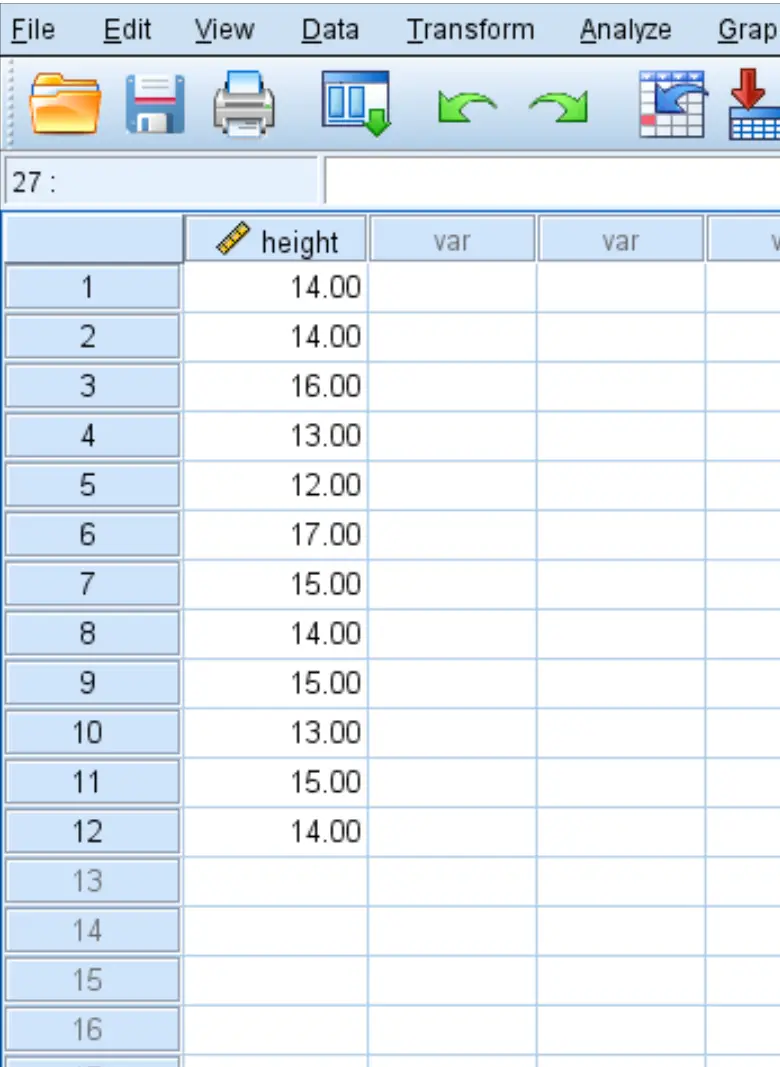
Виконайте наступні кроки, щоб виконати t-критерій для однієї вибірки, щоб визначити, чи справжня середня висота цього виду рослин дорівнює 15 дюймам, на основі таких нульових та альтернативних гіпотез:

• H ₀ : μ = 15 (реальне середнє значення населення дорівнює 15 дюймам)
• H ₁ : μ ≠ 15 (справжня середня популяція не дорівнює 15 дюймам)

Використовуйте рівень значущості α = 0,05.

Крок 1. Виберіть варіант t-критерію для однієї вибірки.

Клацніть вкладку «Аналіз» , потім «Порівняти середні» , а потім «Т-тест з одним зразком» :

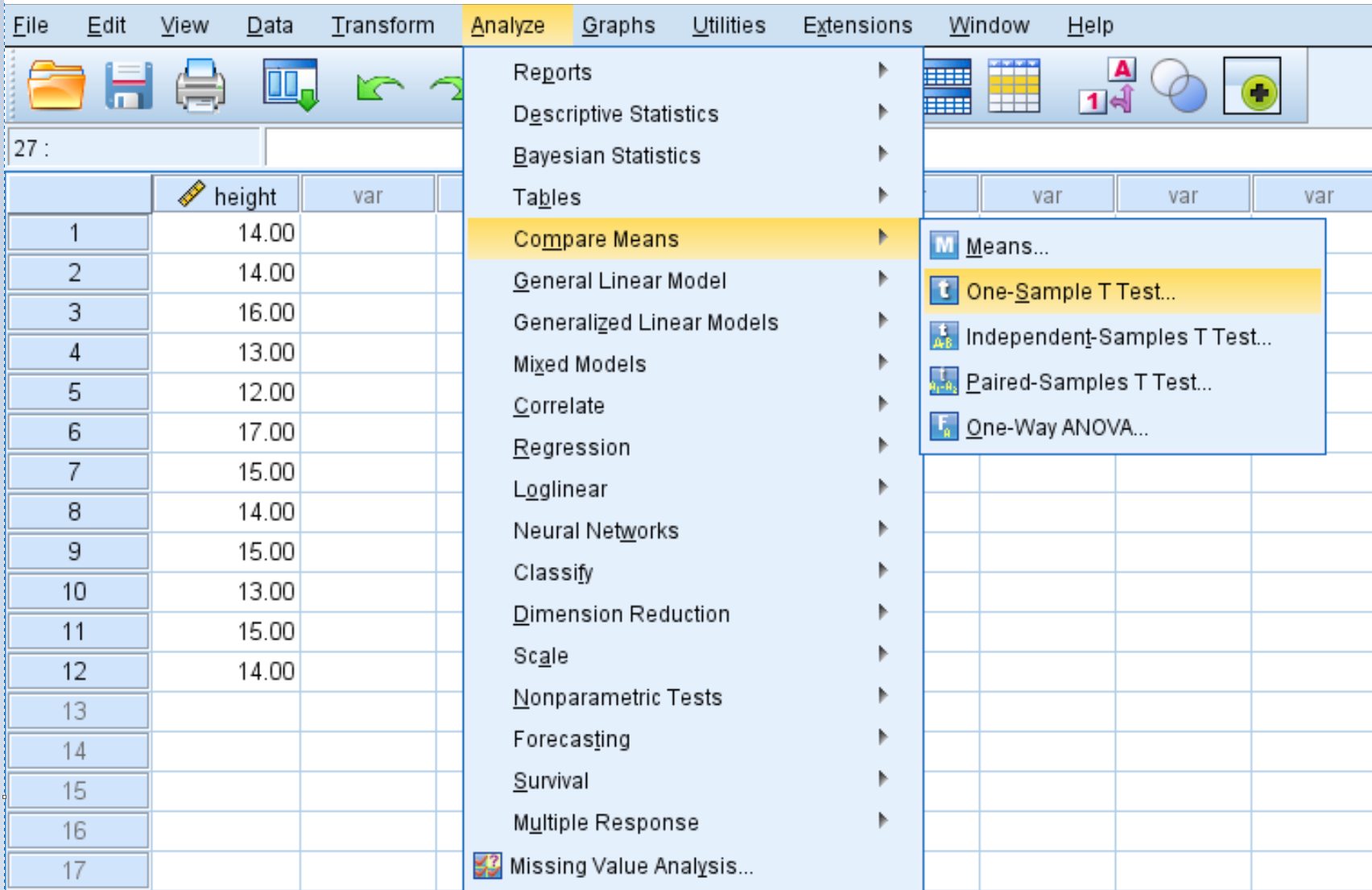
Крок 2: Заповніть значення, необхідні для виконання одновибіркового t-критерію.

Після того, як ви натиснете One-Sample T Test , з’явиться таке вікно:

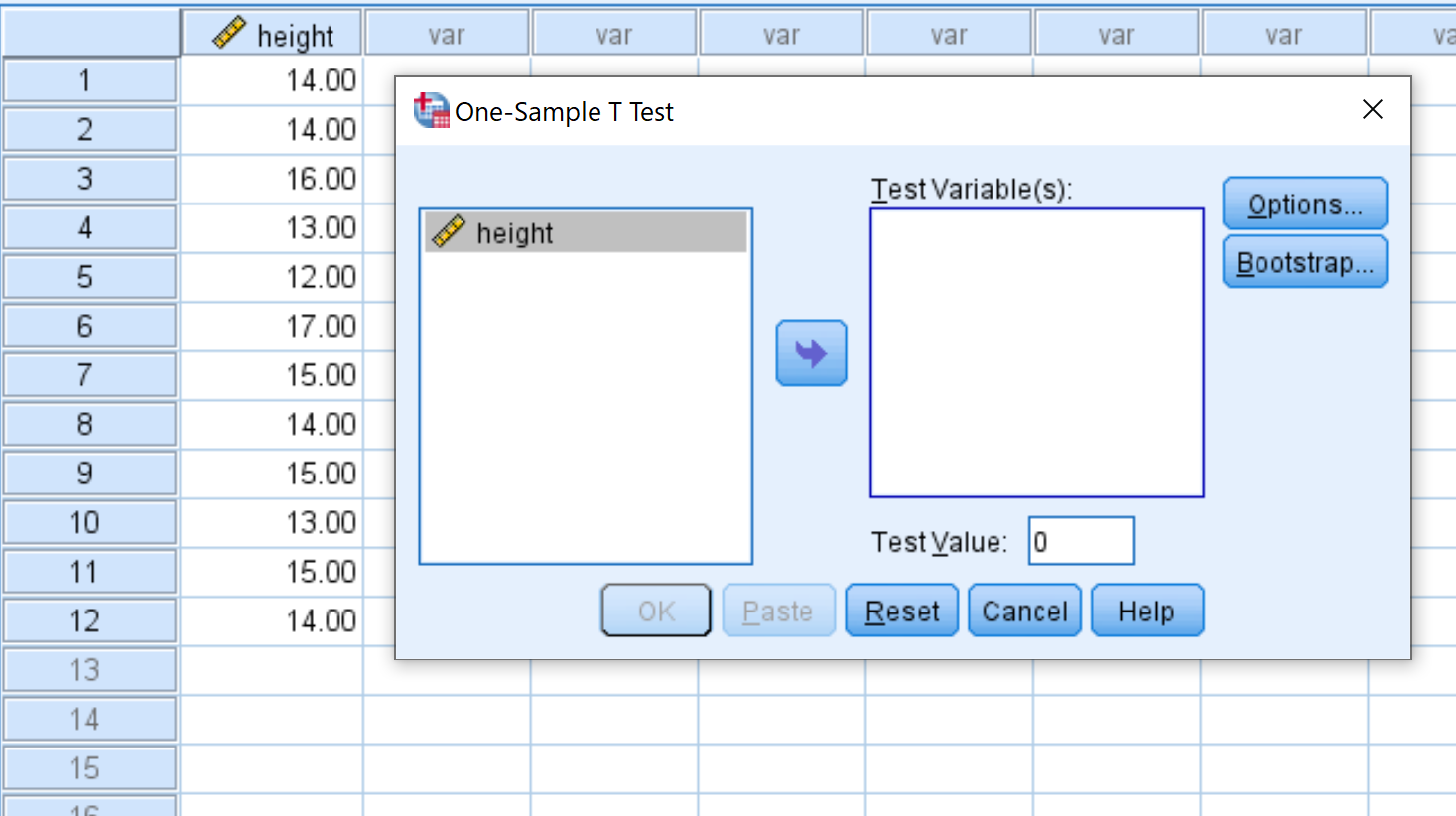
Перетягніть висоту змінної в поле з написом Test Variable(s) і змініть Test Value на 15. Потім натисніть OK .

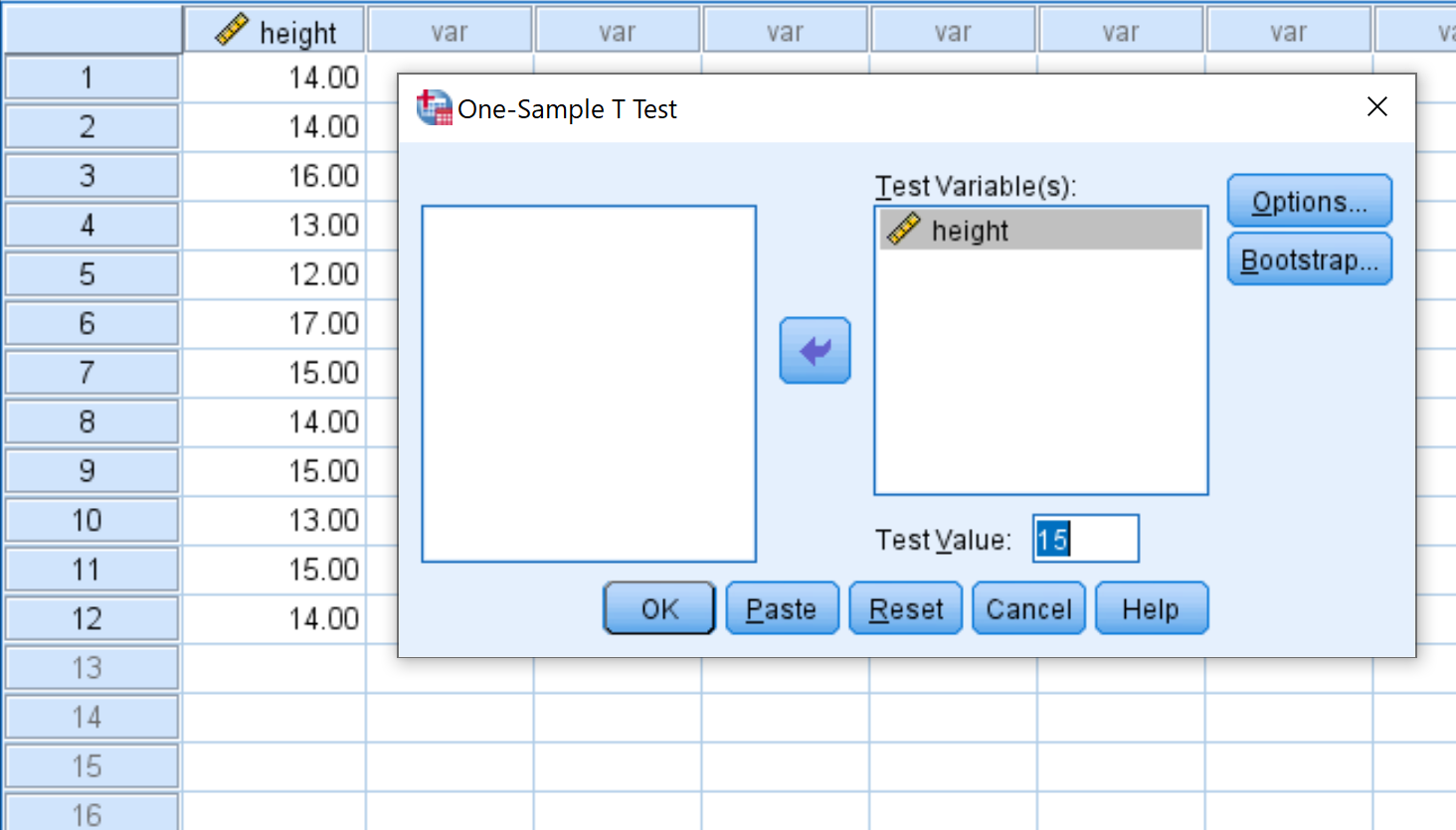
Крок 3: Інтерпретація результатів.

Після натискання кнопки OK відобразяться результати t-критерію для однієї вибірки:

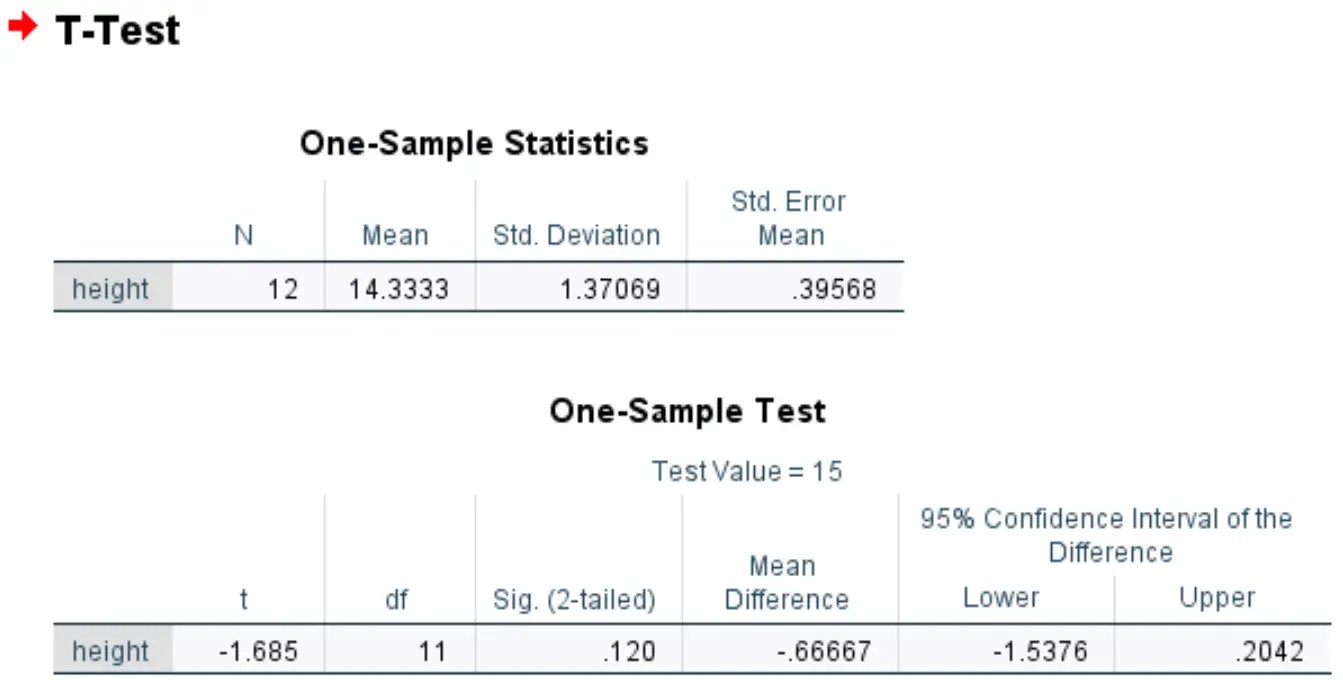
Перша таблиця відображає підсумкову статистику для змінної висоти:

• N: Розмір вибірки
• Середнє значення: середня висота рослин у зразку
• Стандартний. Відхилення: стандартне відхилення висоти рослини у зразку.
• Стандартний. Середня похибка: стандартна похибка середнього, розрахована як s/√n

Друга таблиця відображає результати t-тесту для однієї вибірки:

• t: Статистика тесту, розрахована як (x – μ) / (s/√n) = (14,3333-15) / (1,37/√12) = -1,685
• df: Ступені свободи, розраховані як n-1 = 12-1 = 11
• Sig. (двостороннє): двостороннє p-значення, яке відповідає значенню -1,685 з df=11
• Середня різниця: різниця між середнім значенням вибірки та гіпотетичним середнім
• 95% ДІ різниці: 95% довірчий інтервал для справжньої різниці між середнім значенням вибірки та гіпотетичним середнім.

Оскільки p-значення тесту (0,120) не менше 0,05, ми не можемо відхилити нульову гіпотезу. У нас недостатньо доказів, щоб стверджувати, що справжня середня висота цього виду рослини є чимось іншим, ніж 15 дюймів.